Модуля 1

Конспект лекций

«Основные модели и алгоритмы проектирования в САПР СБИС»

дисциплины
«Базовые модели и алгоритмы в САПР СБИС»

для подготовки магистров по ООП НИУ
«Физическое проектирование микро и нанометровых САПР СБИС»

профиль «Системы автоматизированного проектирования»

Лекция 1 Цели и задачи учебного курса. Построение (план работы) учебного курса. Оценка сложности алгоритмов. О-нотация. Связь структур данных и сложности алгоритмов. Связь структур данных с потреблением памяти. O(n), O(log n), O(n2), O(n3), exp – примеры задач и структур данных.

Содержание:

1. Оценка сложности алгоритмов.

2. Вычислительная сложность.

3. Пространственная сложность.

4. О-нотация.

5. Связь структур данных со сложностью алгоритмов.

6. O(n), O(log n), O(n²), O(n³), O(exp n) классы сложности.

7. Средства языка C.

8. Примеры задач и структур данных.

В информатике, теория сложности вычислений является разделом теории вычислений, изучающим стоимость работы, требуемой для решения вычислительной проблемы. Стоимость обычно измеряется абстрактными понятиями времени и пространства, называемыми вычислительными ресурсами. Время определяется количеством элементарных шагов, необходимых для решения проблемы, тогда как пространство определяется объёмом памяти или места на носителе данных. Таким образом, в этой области предпринимается попытка ответить на центральный вопрос разработки алгоритмов: «как изменится время исполнения и объём занятой памяти в зависимости от размера входа и выхода?». Здесь под размером входа понимается длина описания данных задачи в битах (например, в задаче коммивояжера длина входа пропорциональна количеству городов и дорог между ними), а под размером выхода — длина описания решения задачи (оптимального маршрута в задаче коммивояжера).

В частности, теория сложности вычислений определяет NP-полные задачи, которые недетерминированная машина Тьюринга может решить за полиномиальное время, тогда как для детерминированной машины Тьюринга полиномиальный алгоритм неизвестен. Обычно это сложные проблемы оптимизации, например, задача коммивояжера.

Важность оценки сложности алгоритма проявляется на этапе выбора алгоритма необходимого для решения задачи. Такая оценка позволяет оценить количество ресурсов, которое будет использовать алгоритм и сопоставить его с имеющимися ресурсами. Любая инженерная задача – это задача компромиссов. Пространственная и вычислительная сложности алгоритма зачастую сильно связаны, и уменьшение одной из них ведет к увеличению другой. Как правило, различные алгоритмы отличаются этим отношением. Для любой задачи можно привести вырожденный пример, обладающий максимальной вычислительной или пространственной сложностью и практически нулевой второй составляющей.

Оценка сложности алгоритмов – это всего лишь первое приближение. Другими решающими факторами могут оказаться – специфические характеристики наборов данных, архитектурные вариации компьютеров (кэши различных уровней, механизмы ввода-вывода) и особенности реализации на целевой программной платформе. Зачастую алгоритм, проигрывающий по оценочной характеристике, на реальных задачах и программно-аппаратных комплексах показывает лучшие результаты. Поэтому теоретическую оценку всегда надо рассматривать совместно с целевой платформой и ее особенностями.

При оценке вычислительной сложности, кроме общего количества выполняемых элементарных действий следует рассматривать так же конвейеризацию инструкций, многоядерные и многопроцессорные системы, векторные процессоры, особенности набора инструкций, предсказание ветвлений и другие особенности, которые свойственны современным компьютерным системам.

При оценке пространственной сложности стоит учитывать виртуализацию памяти, размер системных буферов и кэшей, наличие и необходимость использования внешних носителей данных, в т.ч. сетевого транспорта.

«O» большое и «o» малое (O и o) — математические обозначения для сравнения асимптотического поведения функций. Используются в различных разделах математики, но активнее всего — в математическом анализе, теории чисел и комбинаторике, а также при оценке сложности алгоритмов. В частности, фраза «сложность алгоритма есть O(n!)» означает, что при больших n время работы алгоритма (или общее количество операций) не более чем C · n!, где C — некая положительная константа (обычно в качестве параметра n берут объём входной информации алгоритма).

Количество элементарных операций, затраченных алгоритмом для решения конкретного экземпляра задачи, зависит не только от размера входных данных, но и от самих данных. Например, количество операций алгоритма сортировки вставками значительно меньше в случае, если входные данные уже отсортированы. Чтобы избежать подобных трудностей, рассматривают понятие временной сложности алгоритма в худшем случае.

Временная сложность алгоритма (в худшем случае) — это функция размера входных и выходных данных, равная максимальному количеству элементарных операций, проделываемых алгоритмом для решения экземпляра задачи указанного размера. В задачах, где размер выхода не превосходит или пропорционален размеру входа, можно рассматривать временную сложность как функцию размера только входных данных.

Аналогично понятию временной сложности в худшем случае определяется понятие временная сложность алгоритма в наилучшем случае. Также рассматривают понятие среднее время работы алгоритма, то есть математическое ожидание времени работы алгоритма. Иногда говорят просто: «Временная сложность алгоритма» или «Время работы алгоритма», имея в виду временную сложность алгоритма в худшем, наилучшем или среднем случае (в зависимости от контекста).

По аналогии с временной сложностью, определяют пространственную сложность алгоритма, только здесь говорят не о количестве элементарных операций, а об объёме используемой памяти.

Примеры:

«пропылесосить ковер» требует время, линейно зависящее от его площади (O(A)), то есть на ковер, площадь которого больше в два раза, уйдет в два раза больше времени. Соответственно, при увеличении площади ковра в сто тысяч раз, объем работы увеличивается строго пропорционально в сто тысяч раз, и т. п.

«найти имя в телефонной книге» требует всего лишь время, логарифмически зависящее от количества записей (O(log₂(n))), так как открыв книгу примерно в середине, мы уменьшаем размер «оставшейся проблемы» вдвое (за счет сортировки имен по алфавиту). Таким образом, в книге, толщиной в 1000 страниц, любое имя находится не больше чем за 10 раз (открываний книги). При увеличении объема страниц до ста тысяч, проблема все еще решается за 17 заходов.

Как видно из последнего примера, сложность алгоритмов (и пространственная и вычислительная) сильно зависит от представления данных, т.е. от их структуры и расположения в памяти. Наряду с алгоритмами, структуры данных являются одним из двух важнейших компонентов программ. В дальнейшем мы увидим эту связь на наглядных примерах для каждого класса сложности.

Как мы уже узнали, оценка O не всегда однозначно описывает сложность алгоритма, так как не учитывает программно-аппаратные особенности среды исполнения. Кроме того, такая оценка верна только для очень больших n, а так же для измерения деградации – увеличения потребления ресурсов с ростом количества входных данных. Для фиксированных средних размеров данных, ценность этой оценки сильно снижается, поскольку сильное влияние оказывает опущенная константа C. Поэтому говорят не о сложности алгоритма, а о классе сложности, к которому он относится.

Класс сложности O(c) – константная сложность. Это класс самых быстрых и не требовательных к памяти алгоритмов. Сложность алгоритмов этого класса не зависит от количества входных данных. Такой операцией например является получение элемента массива по его индексу. Ведь не важно, сколько элементов содержится в массиве, мы всегда можем узнать где находится искомый элемент, просто прибавив его смещение к началу массива.

Класс сложности O(log n) – логарифмическая зависимость. Примером такой зависимости является поиск в предварительно отсортированном массиве. Такая зависимость считается одной из наиболее слабых. Даже при сильном увеличении размера входных данных время выполнения или объем потребляемой памяти увеличиваются незначительно. Как правило, такая зависимость характерна для вычислительной сложности, поскольку пространственная сложность ниже линейной подразумевает сжатие данных. Интересным примером логарифмической зависимости являются числа в позиционной системе счисления. Увеличение числа на один разряд приводит к увеличению возможных значений числа на порядок.

Класс сложности O(n) – линейная зависимость времени выполнения или потребления памяти от количества входных данных. Важно не забывать про константу C, при значениях которой, сравнимых с n, алгоритмы этого класса не отличаются от алгоритмов более высокого класса сложности. Примером алгоритма данного класса сложности является последовательный перебор элементов массива или списка.

Класс сложности O(n²) – квадратичная зависимость. Такая зависимость означает для вычислительной сложности, что каждый элемент входного набора подвергается числу операций, зависящему от размера входного множества. Примером такого алгоритма является поиск элементов одного списка в другом. Интересно отметить, что класс сложности зависит от того, что мы считаем входными данными. Например операция поиска элемента матрицы имеет класс сложности O(n), если n – число элементов и O(n²), если n – размерность матрицы.

Класс сложности O(n³) – кубическая зависимость, класс сложности, часто встречающийся в задачах топологического проектирования. Зачастую задачи такого проектирования сводятся к неким операциям над фигурами на плоскости. Для того чтобы снизить сложность задачи, ее разбивают на операции относительно двух перпендикулярных осей, что дает квадратичную сложность для наивного алгоритма, если мы вспомним что число элементов топологии примерно пропорционально числу мест для их размещения, то для всей задачи мы получим кубическую зависимость.

Класс сложности O(n!) и O(exp n) – такая сложность характерна для задач перебора, когда все пространство решения отображается в память или разворачивается во время выполнения. Обычно алгоритмы, относящиеся к такому классу сложности, применяют для первичной оценки решения задачи и как эталоны для оценки худшего по затратам ресурсов случая.

Для наглядной демонстрации примеров алгоритмов мы будем в дальнейшем использовать язык Си из-за его простоты и распространенности.

Рассмотрим несколько примеров структур данных, которые позволят нам изменять класс сложности алгоритма.

int *arr = (int *)malloc (10);

Это обычный массив, он удобен тем, что операция доступа к любому элементу массива осуществляется за постоянное время. Однако если мы захотим вставить элемент в середину массива, нам понадобится выделить память для нового массива увеличенной длины, скопировать туда все элементы старого массива, оставив место для вставляемого элемента, а потом вставить его:

int* new_arr = (int*)malloc(11);

int i = 0;

for (i = 0; i < new_pos; i++)

new_arr[i] = arr[i];

new_arr[new_pos] = new_el;

for (i = new_pos + 1; i < 11; i++)

new_arr[i] = arr[i-1];

Мало того, что такой код будет долго выполнятся, он предрасположен к большому количеству ошибок.

Если в нашей программе данные часто добавляются, то лучшей структурой будет связанный список:

typedef list_node_t {

int value;

list_node* next;

} list_node;

Рисунок 1 Связанный список.

Такая структура позволяет легко добавлять и удалять элементы за константное время, однако для того чтобы найти какой-либо элемент по-прежнему требуется пройти весь список. Для того чтобы облегчить поиск списки делают двунаправленными, но еще более сложной структурой, позволяющей в лучшем случае (заметим, что для оценки используются слова в лучшем и худшем случае, поскольку эффективность структур данных, более сложных чем простые списки и массивы, сильно зависит от характеристик входных данных) обеспечить константную сложность вставки, удаления и поиска является хеш-таблица.

Хеш-таблица – это структура данных, реализующая интерфейс ассоциативного массива, а именно, она позволяет хранить пары (ключ, значение) и выполнять три операции: операцию добавления новой пары, операцию поиска и операцию удаления пары по ключу.

Существует два основных варианта хеш-таблиц: с цепочками и открытой адресацией. Хеш-таблица содержит некоторый массив, элементы которого есть пары (хеш-таблица с открытой адресацией) или списки пар (хеш-таблица с цепочками).

Выполнение операции в хеш-таблице начинается с вычисления хеш-функции от ключа. Получающееся хеш-значение i = hash(key) играет роль индекса в массиве. Затем выполняемая операция (добавление, удаление или поиск) перенаправляется объекту, который хранится в соответствующей ячейке массива.

Ситуация, когда для различных ключей получается одно и то же хеш-значение, называется коллизией. Такие события не так уж и редки – например, при вставке в хеш-таблицу размером 365 ячеек всего лишь 23-х элементов вероятность коллизии уже превысит 50 % (если каждый элемент может равновероятно попасть в любую ячейку). Поэтому механизм разрешения коллизий – важная составляющая любой хеш-таблицы.

В некоторых специальных случаях удаётся избежать коллизий вообще. Например, если все ключи элементов известны заранее (или очень редко меняются), то для них можно найти некоторую совершенную хеш-функцию, которая распределит их по ячейкам хеш-таблицы без коллизий. Хеш-таблицы, использующие подобные хеш-функции, не нуждаются в механизме разрешения коллизий, и называются хеш-таблицами с прямой адресацией.

Число хранимых элементов, делённое на размер массива (число возможных значений хеш-функции), называется коэффициентом заполнения хеш-таблицы (load factor) и является важным параметром, от которого зависит среднее время выполнения операций.

Важное свойство хеш-таблиц состоит в том, что, при некоторых разумных допущениях, все три операции (поиск, вставка, удаление элементов) в среднем выполняются за время O(1). Но при этом не гарантируется, что время выполнения отдельной операции мало. Это связано с тем, что при достижении некоторого значения коэффициента заполнения необходимо осуществлять перестройку индекса хеш-таблицы: увеличить значение размера массива и заново добавить в пустую хеш-таблицу все пары.

Рисунок 2 Устранение коллизий с помощью связанных списков.

Практический пример:

Для отображения графов зачастую используются матрицы смежности и инцидентности. Рассмотрим граф:

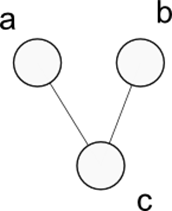
Рисунок 3 Простой граф.

Матрица смежности для него будет выглядеть следующим образом:

	a	b	c
a
b
c

Такое представление достаточно эффективно и позволяет за константное время определить какие из вершин графа связаны. Но предположим что мы работаем в системе с ограничением памяти. Рассмотрим пространственную сложность такого представления графа.

Для того чтобы представить граф с тремя вершинами нам понадобилось 9 бит, для графа с четыремя вершинами их будет уже 16 и так далее. Легко понять, что пространственный класс сложности данного представления – O(n²). Для характерного графа электрической схемы, состоящей из миллиона вентилей, матрица смежности займет 10¹² бит – или около терабайта памяти!

Однако представим граф в виде набора списков:

a->c

b->c

c->a,b

Несмотря на то, что для приведенного примера памяти потребовалось больше (посчитайте сами сколько), пространственный класс сложности данной структуры составляет O(n+m), где m – число ребер, которое как правило пропорционально числу вершин для электрических схем. Поэтому для той же схемы из миллиона элементов такая структура займет всего несколько мегабайт (несколько из-за константы, которая не упоминается в O-нотации).

Вопросы и задания для самостоятельной проработки:

1. Какие бы хеш-функции вы бы предложили для строковых значений? Для целочисленных значений?[2, гл.11]

2. Оцените пространственную и вычислительную сложность алгоритма сортировки пузырьком. [4]

3. Разработайте механизм автоматической генерации «совершенной» хеш-функции для заданного набора целых чисел. [2]

4. Подумайте, как можно найти циклы в связном списке.[5]

5. Какова временная и пространственная сложность вашего предложения?[4]

6. Предложите экстремальные случаи алгоритма поиска циклов – один для минимизации пространственной сложности, другой – для минимизации вычислительной сложности.

Список литературы:

1. Д. Грин, Д. Кнут Математические методы анализа алгоритмов.

2. Кормен, Т., и другие, Алгоритмы: построение и анализ.

3. Дж. Макконелл Основы современных алгоритмов.

4. http://ips.ifmo.ru/courses/course1/chA/l2/index.html

5. http://www.codenet.ru/progr/cpp/dlist.php

Лекция 2 Полиномиальная сложность. Неполиномиальная сложность. NP-полнота задачи. Классы P и NP. Проблема P=NP.

Содержание:

1. Классы сложности и полные задачи.

2. Иерархия классов сложности.

3. Обозначения классов сложности.

4. Класс сложности P.

5. Класс сложности NP.

6. Примеры задач класса NP.

7. Проблема P=NP.

В теории алгоритмов классами сложности называются множества вычислительных задач, примерно одинаковых по сложности вычисления. Говоря более узко, классы сложности — это множества предикатов (функций, получающих на вход слово и возвращающих ответ 0 или 1), использующих для вычисления примерно одинаковое количества ресурсов.

Для каждого класса существует категория задач, которые являются «самыми сложными». Это означает, что любая задача из класса сводится к такой задаче, и притом сама задача лежит в классе. Такие задачи называют полными задачами для данного класса. Наиболее известными являются NP-полные задачи.

Полные задачи — хороший инструмент для доказательства равенства классов. Достаточно для одной такой задачи предоставить алгоритм, решающий её и принадлежащий более маленькому классу, и равенство будет доказано.

Каждый класс сложности (в узком смысле) определяется как множество предикатов, обладающих некоторыми свойствами. Типичное определение класса сложности выглядит так:

Классом сложности X называется множество предикатов P(x), вычислимых на машинах Тьюринга и использующих для вычисления O(f(n)) ресурса, где n — длина слова x.

Рисунок 4 Иерархия классов сложности.

В качестве ресурсов обычно берутся время вычисления (количество рабочих тактов машины Тьюринга) или рабочая зона (количество использованных ячеек на ленте во время работы). Языки, распознаваемые предикатами из некоторого класса (то есть множества слов, на которых предикат возвращает 1), также называются принадлежащими тому же классу.

Кроме того, многие классы могут также быть описаны в терминах математической логики или теории игр.

Классы принято обозначать прописными буквами. Дополнение к классу C (то есть класс языков, дополнения которых принадлежат C) обозначается co-C.

Рассмотрим функцию f и входную цепочку длиной n. Тогда класс DTIME(f(n)) определяют как класс языков, принимаемых детерминированными машинами Тьюринга, заканчивающими свою работу за время, не превосходящее f(n). Класс NTIME(f(n)), в свою очередь, определяют как класс языков, принимаемых недетерминированной машиной Тьюринга, заканчивающими свою работу за время, не превосходящее f(n). Отметим, что ограничения на память при определении данных классов отсутствуют.

Аналогично иерархии по времени вводится иерархия по памяти. Класс DSPACE(f(n)) обозначает класс языков, принимаемых детерминированными машинами Тьюринга, использующих не более f(n) ячеек памяти на рабочих лентах. Класс NSPACE(f(n)) определяют как класс языков, принимаемых недетерминированными машинами Тьюринга, использующих не более f(n) ячеек памяти на рабочих лентах. Временные ограничения при определении данных классов отсутствуют.

Аналогично определяются и другие подобные рассмотренным выше классы. Приведем использующиеся сокращения:

· D - детерминированный (детерминистический)

· N - недетерминированный

· R - вероятностный с ограниченной односторонней ошибкой

· B - вероятностный с ограниченной двусторонней ошибкой

· BQ - квантовый с ограниченной двусторонней ошибкой

В теории алгоритмов классом P (от англ. polynomial) называют множество задач, для которых существуют «быстрые» алгоритмы решения (время работы которых полиномиально зависит от размера входных данных). Класс P включён в более широкие классы сложности алгоритмов.

Примерами задач из класса P являются целочисленное сложение, умножение, деление, взятие остатка от деления, умножения матриц, выяснение связности графов и некоторые другие.

Поскольку часто приходится вычислять значения функций на входных данных большого объёма, нахождение полиномиальных алгоритмов для вычисления функций является очень важной задачей. Считается, что вычислять функции, не лежащие в классе P, заметно сложнее, чем лежащие. Большинство алгоритмов, лежащих в классе P, имеют сложность, не превосходящую многочлен небольшой степени от размера входных данных. Например, стандартный алгоритм перемножения матриц требует n³ умножений (хотя существуют и более быстрые алгоритмы, например, алгоритм Штрассена). Степень многочлена редко бывает большой. Один из таких случаев — предложенный в 2002 году индийскими математиками тест Агравала — Каяла — Саксены, выясняющий, является ли число n простым, за O(log⁶n) операций.

В теории алгоритмов классом NP (от англ. non-deterministic polynomial) называют множество задач распознавания, решение которых при наличии некоторых дополнительных сведений (так называемого сертификата решения) можно «быстро» (за время, не превосходящее полинома от размера данных) проверить на машине Тьюринга.

Эквивалентно класс NP можно определить как содержащий задачи, которые можно «быстро» решить на недетерминированной машине Тьюринга.

Можно привести много задач, про которые на сегодняшний день неизвестно, принадлежат ли они P, но известно, что они принадлежат NP. Среди них:

· Задача выполнимости булевых формул: узнать по данной булевой формуле, существует ли набор входящих в неё переменных, обращающий её в 1. Сертификат — такой набор.

· Задача о клике: по данному графу узнать, есть ли в нём клики (полные подграфы) заданного размера. Сертификат — номера вершин, образующих клику.

· Определение наличия в графе гамильтонова цикла. Сертификат — последовательность вершин, образующих гамильтонов цикл.

· Задача о коммивояжёре — расширенный и более приближенный к реальности вариант предыдущей задачи.

· Существование целочисленного решения у заданной системы линейных неравенств. Сертификат — решение.

Среди всех задач класса NP можно выделить «самые сложные» — NP-полные задачи. Если удастся решить любую из них за полиномиальное время, то все задачи класса NP также можно будет решить за полиномиальное время.

В теории алгоритмов вопрос о равенстве классов сложности P и NP является одной из центральных открытых проблем уже более трех десятилетий. Если на него будет дан утвердительный ответ, это будет означать, что теоретически возможно решать многие сложные задачи существенно быстрее, чем сейчас.

Проблема равенства классов P и NP является одной из семи задач тысячелетия, за решение которой Математический институт Клэя назначил премию в миллион долларов США.

В конечном счете проблема P = NP состоит в следующем: если положительный ответ на какой-то вопрос можно быстро проверить (за полиномиальное время), то правда ли, что ответ на этот вопрос можно быстро найти (за полиномиальное время и используя полиномиальную память)?

Неформально говоря, действительно ли решение задачи легче проверить, нежели отыскать?

Например, верно ли, что среди чисел {−2, −3, 15, 14, 7, −10, …} есть такие, что их сумма равна 0 (задача о суммах подмножеств)? Ответ да, потому что −2 −3 + 15 −10 = 0 легко проверяется несколькими сложениями (информация, необходимая для проверки положительного ответа, называется сертификатом). Следует ли отсюда, что так же легко установить существование этих чисел в заданном ряду?

Другими словами: правда ли, что для вопроса, разбивающегося на больше-чем-полиномиально растущее количество подвопросов, можно быстро показать (за полиномиальное время) существование положительного ответа на хотя бы один из них, если положительный ответ на такой подвопрос можно быстро проверить?

Практический пример:

При выборе набора компонентов для проектирования электронной схемы из некоторого базиса обычно стараются подобрать минимальное число компонентов, решающих поставленную задачу. При этом стараются выбирать компоненты, реализующие как можно более сложные логические функции, чтобы избежать дополнительных затрат трассировочных ресурсов. При имеющемся фиксированном наборе компонентов задача состоит в выборе его оптимального подмножества и относится к классу NP. Зная это, мы можем не искать детерминированного алгоритма выбора компонента, а сразу подбирать эвристический или алгоритм численной оптимизации.

Вопросы и задания для самостоятельной проработки:

1. Как вы определите полноту задачи, ели известно, к какому классу сложности она принадлежит? [1, гл.8]

2. К какому классу относится задача поиска элемента в связном списке P или NP?[1]

3. Какие средства применяются в алгоритме Штрассена для снижения сложности задачи перемножения матриц? [2, гл.28]

Список литературы:

1. Джон Хопкрофт, Раджив Мотвани, Джеффри Ульман, Введение в теорию автоматов, языков и вычислений.

2. Кормен, Т., и другие, Алгоритмы: построение и анализ.

3. ftp://ftp.mccme.ru/users/vyalyi/qcomp/qbook.ps.gz

4. http://www.cs.umd.edu/~gasarch/papers/poll.pdf

Лекция 3 Списки. Очереди. Стеки. Массивы. Хэш-таблицы. Куча. Кольцевой буфер. Алгоритмы сортировки. Алгоритмы поиска, модификации. Методы распределения памяти. Паттерны RAII и PIMPL.

Содержание:

1. Односвязный список.

2. Очередь.

3. Стек.

4. Хеш-таблица.

5. Куча.

6. Кольцевой буфер.

7. Классификация алгоритмов сортировки.

Линейный однонаправленный список — это структура данных, состоящая из элементов одного типа, связанных между собой.

Рисунок 5 Односвязный список.

В информатике линейный список обычно определяется как абстрактный тип данных (АТД), формализующий понятие упорядоченной коллекции данных.

На практике линейные списки обычно реализуются при помощи массивов и связных списков. Иногда термин «список» неформально используется также как синоним понятия «связный список».

К примеру, АТД нетипизированного изменяемого списка может быть определён как набор из конструктора и четырёх основных операций:

1. операция, проверяющая список на пустоту;

2. операция добавления объекта в список;

3. операция определения первого (головного) элемента списка;

4. операция доступа к списку, состоящему из всех элементов исходного списка, кроме первого.

Рисунок 6 Реализация связного списка с помощью массива.

Самой простой реализацией списка будет его реализация с помощью массива. Вспомним, что память компьютера – это огромный непрерывный массив, а указатели – всего лишь индексы в этом массиве. Теперь представим список на рисунке 6 в виде двух массивов:

int data[LIST_LENGTH];

int p[LIST_LENGTH];

В первом массиве мы будем хранить полезную информацию – элементы списка, а во втором будет индекс элемента, следующего за текущим. Нам понадобится так же индекс головы списка(это необходимо, поскольку мы можем удалить головной элемент и тогда головным элементом станет элемент с индексом 1):

int head = 0;

Заметим, что конец списка обозначен -1. В реализации списка с указателями используется такой же принцип «указателя, который никуда не указывает». Мы еще не раз столкнемся с этой полезной концепцией особого нулевого элемента.

Попробуем теперь реализовать операции, перечисленные нами выше.

Проверка списка на пустоту достаточна тривиальна:

if(head == -1)

return 1;

else

return 0;

Действительно, если за головой не следует ни одного элемента, то список пуст.

Теперь попробуем добавить объект в список. Для этого нам понадобится свободное место. Модифицируем список, как показано на рисунке 7.

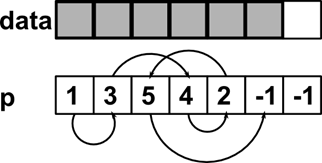
Рисунок 7 Пустое место в списке.

Для начала нам нужно выделить память. Если бы наш список использовал указатели, эту задачу можно поручить менеджеру памяти и просто вызвать malloc, однако в нашей простой реализации это требуется делать вручную.

Добавим элемент в конец массива данных. Будем добавлять его в голову списка.

int idx = LIST_LENGTH – 1;

data[idx] = new_data;

Сначала выставим указатель таким образом, чтобы он указывал на старую голову:

p[idx] = head;

Теперь установим новую голову списка:

head = idx;

Вот и все! Список теперь содержит новый элемент и выглядит согласно рисунку 8.

Рисунок 8 Список со вставленным элементом.

Доступ к головному элементу тривиален, нам просто нужно прочитать элемент по индексу head:

data[head];

Для того чтобы получить список, состоящий из всех элементов списка кроме головного, вспомним чем определяется список – индексом головного элемента. Индексом головного элемента искомого списка будет индекс второго элемента списка, поэтому эта операция тоже тривиальна:

head2 = p[head];

Итак, наша реализация полностью соответствует интерфейсу.

Очередь — структура данных с дисциплиной доступа к элементам «первый пришёл — первый вышел» (FIFO, First In — First Out). Добавление элемента (принято обозначать словом enqueue — поставить в очередь) возможно лишь в конец очереди, выборка — только из начала очереди (что принято называть словом dequeue — убрать из очереди), при этом выбранный элемент из очереди удаляется.

Поскольку очередь является АТД, не определяется никаких ограничений в реализации. Попробуем построить очередь поверх описанного выше связного списка. Кроме индекса головы списка будем хранить индекс хвоста списка. Начнем с пустого списка:

Рисунок 9 Пустая очередь.

Голова списка и его хвост указывают вне списка. Иногда чтобы все операции над списками выглядели одинаково, вводят специальный пустой элемент. В таком случае голова и хвост будут указывать на этот пустой элемент.

int head = -1;

int tail = -1;

Попробуем добавить элемент:

data[new_idx] = new_el;

if (tail!= -1) {

p[tail] = new_idx;

}

tail = new_idx;

if (head == -1) {

head = new_idx;

}

После нескольких вставок очередь будет выглядеть так же, как на рисунке 10.

Рисунок 10 Очередь с несколькими элементами.

Теперь попробуем удалить элемент. Поскольку мы вставляли элементы с хвоста, то чтобы реализовать семантику очереди, удалять будем из головы.

if (head!= -1) {

int result = data[head];

head = p[head];

return result;

} else {

// Ошибка, очередь пуста

};

Использование связного списка упростило нам задачу, поскольку список может расти в обе стороны, что позволяет нам получать и принимать элементы на противоположных концах. Однако если отказаться от такого свойства очереди, то мы можем существенно упростить реализацию. Такая структура называется стек.

Стек (англ. stack – стопка) – структура данных, в которой доступ к элементам организован по принципу LIFO (англ. last in – first out, «последним пришёл – первым вышел»). Чаще всего принцип работы стека сравнивают со стопкой тарелок: чтобы взять вторую сверху, нужно снять верхнюю.

Добавление элемента, называемое также проталкиванием (push), возможно только в вершину стека (добавленный элемент становится первым сверху). Удаление элемента, называемое также выталкиванием (pop), тоже возможно только из вершины стека, при этом второй сверху элемент становится верхним.

Стеки широко применяются в вычислительной технике. Например, для отслеживания точек возврата из подпрограмм используется стек вызовов, который является неотъемлемой частью архитектуры большинства современных процессоров. Языки программирования высокого уровня также используют стек вызовов для передачи параметров при вызове процедур.

Арифметические сопроцессоры, программируемые микрокалькуляторы и язык Forth используют стековую модель вычислений.

Как мы увидим, реализация стека гораздо проще очереди, что и обусловило его столь широкое использование.

Начнем с создания простого массива и двух переменных.

int data[STACK_SIZE];

int top = 0;

int bottom = 0;

Полученная структура представлена на рисунке 11.

Рисунок 11 Пустой стек.

Добавление элемента в стек (проталкивание, push), заключается в следующем: сначала мы помещаем новый элемент в позицию top (на вершину стека), а затем смещаем вершину в новое положение:

data[top] = new_el;

top++;

После того, как мы несколько раз выполним операцию, стек приобретает вид:

Рисунок 12 Стек после нескольких проталкиваний.

Для удаления элемента из стека (выталкивания, pop) требуется проделать обратную процедуру:

if (top!= bottom) {

int result = data[top];

top--;

} else {

// Ошибка, стек пуст.

};

bottom используется в тех случаях, когда мы хотим предотвратить доступ к некоторым значениям в стеке, если мы сохраним значение bottom для нашей функции и установим его на вершину стека, то функции, вызванные после этого не смогут получить доступ к «секретным» данным, лежащим ниже bottom. Вместо этого они получат сообщение о том что стек пуст.

Хеш-таблица — это структура данных, реализующая интерфейс ассоциативного массива, а именно, она позволяет хранить пары (ключ, значение) и выполнять три операции: операцию добавления новой пары, операцию поиска и операцию удаления пары по ключу.

Существует два основных варианта хеш-таблиц: с цепочками и открытой адресацией. Хеш-таблица содержит некоторый массив H, элементы которого есть пары (хеш-таблица с открытой адресацией) или списки пар (хеш-таблица с цепочками).

Выполнение операции в хеш-таблице начинается с вычисления хеш-функции от ключа. Получающееся хеш-значение i = hash(key) играет роль индекса в массиве H. Затем выполняемая операция (добавление, удаление или поиск) перенаправляется объекту, который хранится в соответствующей ячейке массива H[i].

Ситуация, когда для различных ключей получается одно и то же хеш-значение, называется коллизией. Такие события не так уж и редки — например, при вставке в хеш-таблицу размером 365 ячеек всего лишь 23-х элементов вероятность коллизии уже превысит 50 % (если каждый элемент может равновероятно попасть в любую ячейку). Поэтому механизм разрешения коллизий — важная составляющая любой хеш-таблицы.

В некоторых специальных случаях удаётся избежать коллизий вообще. Например, если все ключи элементов известны заранее (или очень редко меняются), то для них можно найти некоторую совершенную хеш-функцию, которая распределит их по ячейкам хеш-таблицы без коллизий. Хеш-таблицы, использующие подобные хеш-функции, не нуждаются в механизме разрешения коллизий, и называются хеш-таблицами с прямой адресацией.

Число хранимых элементов, делённое на размер массива H (число возможных значений хеш-функции), называется коэффициентом заполнения хеш-таблицы (load factor) и является важным параметром, от которого зависит среднее время выполнения операций.

Важное свойство хеш-таблиц состоит в том, что, при некоторых разумных допущениях, все три операции (поиск, вставка, удаление элементов) в среднем выполняются за время O(1). Но при этом не гарантируется, что время выполнения отдельной операции мало́. Это связано с тем, что при достижении некоторого значения коэффициента заполнения необходимо осуществлять перестройку индекса хеш-таблицы: увеличить значение размера массива H и заново добавить в пустую хеш-таблицу все пары.

В компьютерных науках куча — это специализированная структура данных типа дерево, которая удовлетворяет свойству кучи: если B является узлом-потомком узла A, то ключ(A) ≥ ключ(B). Из этого следует, что элемент с наибольшим ключом всегда является корневым узлом кучи, поэтому иногда такие кучи называют max-кучами (в качестве альтернативы, если сравнение перевернуть, то наименьший элемент будет всегда корневым узлом, такие кучи называют min-кучами). Не существует никаких ограничений относительно того, сколько узлов-потомков имеет каждый узел кучи, хотя на практике их число обычно не более двух. Куча является максимально эффективной реализацией абстрактного типа данных, который называется очередью с приоритетом. Кучи имеют решающее значение в некоторых эффективных алгоритмах на графах, таких как алгоритм Дейкстры и сортировка методом пирамиды.

Структуру данных куча не следует путать с понятием куча в динамическом распределении памяти. Впервые термин использовался именно для структур данных. В некоторых ранних популярных языках программирования типа ЛИСП обеспечивалось динамическое распределение памяти с использованием структуры данных «куча», которая и дала своё имя выделяемому объёму памяти.

Кучи обычно реализуются в виде массивов, что исключает наличие указателей между её элементами.

Над кучами обычно проводятся следующие операции:

1. найти максимум или найти минимум: найти максимальный элемент в max-куче или минимальный элемент в min-куче, соответственно

2. удалить максимум или удалить минимум: удалить корневой узел в max- или min-куче, соответственно

3. увеличить ключ или уменьшить ключ: обновить ключ в max- или min-куче, соответственно

4. добавить: добавление нового ключа в кучу.

5. слияние: соединение двух куч с целью создания новой кучи, содержащей все элементы обеих исходных.

Кольцевой буфер является разновидностью буфера FIFO, First Input First Output (первый зашел - первый вышел). Принцип кольцевого буфера довольно прост - в памяти выделяется непрерывный блок размером обычно равным степени двойки (назовем его buffer), и два индекса (idxIN и idxOUT) - один индекс указывает на место для записи в буфер (idxIN), другой - на место чтения из буфера.

Алгоритм сортировки — это алгоритм для упорядочения элементов в списке. В случае, когда элемент списка имеет несколько полей, поле, служащее критерием порядка, называется ключом сортировки. На практике в качестве ключа часто выступает число, а в остальных полях хранятся какие-либо данные, никак не влияющие на работу алгоритма.

Классификация алгоритмов сортировки

· Устойчивость (stability) — устойчивая сортировка не меняет взаимного расположения равных элементов.

· Естественность поведения — эффективность метода при обработке уже упорядоченных, или частично упорядоченных данных. Алгоритм ведёт себя естественно, если учитывает эту характеристику входной последовательности и работает лучше.

· Использование операции сравнения. Алгоритмы, использующие для сортировки сравнение элементов между собой, называются основанными на сравнениях. Минимальная трудоемкость худшего случая для этих алгоритмов составляет, но они отличаются гибкостью применения. Для специальных случаев (типов данных) существуют более эффективные алгоритмы.

Ещё одним важным свойством алгоритма является его сфера применения. Здесь основных типов упорядочения два:

Внутренняя сортировка оперирует с массивами, целиком помещающимися в оперативной памяти с произвольным доступом к любой ячейке. Данные обычно упорядочиваются на том же месте, без дополнительных затрат.

В современных архитектурах персональных компьютеров широко применяется подкачка и кэширование памяти. Алгоритм сортировки должен хорошо сочетаться с применяемыми алгоритмами кэширования и подкачки.

Внешняя сортировка оперирует с запоминающими устройствами большого объёма, но с доступом не произвольным, а последовательным (упорядочение файлов), т. е. в данный момент мы 'видим' только один элемент, а затраты на перемотку по сравнению с памятью неоправданно велики. Это накладывает некоторые дополнительные ограничения на алгоритм и приводит к специальным методам упорядочения, обычно использующим дополнительное дисковое пространство. Кроме того, доступ к данным на носителе производится намного медленнее, чем операции с оперативной памятью.

Доступ к носителю осуществляется последовательным образом: в каждый момент времени можно считать или записать только элемент, следующий за текущим.

Также алгоритмы классифицируются по:

· потребности в дополнительной памяти или её отсутствии,

· потребности в знаниях о структуре данных, выходящих за рамки операции сравнения, или отсутствии таковой.

Практический пример:

Во многих реализациях динамического распределения памяти блоки содержатся в связном списке, так называемом «свободном списке». Суть выделения памяти заключается в том, что менеджер памяти хранит указатель на первый свободный блок, а в заголовке каждого такого блока хранится его размер и указатель на следующий блок.

Как только менеджеру поступает запрос на выделение блока памяти, он проходит по списку в поисках подходящего блока. Если такой блок найден, он удаляется из свободного списка. Если же он был больше требуемого размера, то этот блок делится на два, первый возвращается вызывающей программе, а второй добавляется в свободный список на место удаленного.

В качестве самостоятельного упражнения подумайте, как можно повысить устойчивость менеджера памяти к фрагментации – явлению, когда в свободном списке содержится множество мелких элементов, непригодных для выделения памяти под крупный блок, но сумма размеров этих элементов больше требуемого размера.

Вопросы и задания для самостоятельной проработки:

1. Переделайте реализацию связного списка так, чтобы она работала с указателями вместо индексов массивов.[1]

2. Реализуйте кольцевой буфер, используя массив в качестве хранилища данных.[1]

3. Реализуйте механизм устранения коллизий в хеш-таблице с цепочками с помощью массивов и связанных списков.[1]

4. Оцените сложность элементарных операций над стеком, очередью и списком.[1]

5. Подумайте, в каких случаях можно (и нужно) заменить данные в списке указателями на них.[1]

6. Какие еще варианты реализации менеджера памяти, кроме свободного списка приходят вам в голову?[6]

Список литературы:

1. Кормен, Т., и другие, Алгоритмы: построение и анализ.

2. Д. Грин, Д. Кнут Математические методы анализа алгоритмов.

3. http://xlinux.nist.gov/dads//HTML/queue.html

4. http://xlinux.nist.gov/dads//HTML/stack.html

5. http://xlinux.nist.gov/dads//HTML/abstractDataType.html

6. http://www.cs.nyu.edu/faculty/davise/pl/Memory%20Allocation.ppt

Лекция 4 Понятие о графах. Представление графов. Матрицы связности и инцидентности. Основные алгоритмы. Алгоритм Дейкстры. Поиск в ширину. Поиск в глубину. Задача коммивояжера. Граф как модель данных.

Содержание:

1. Граф.

2. Матрица смежности.

3. Матрица инцидентности.

4. Список связности.

5. Основные операции с графом.

6. Поиск в ширину.

7. Поиск в глубину.

8. Алгоритм Дейкстры.

9. Задача коммивояжера.

В математической теории графов и информатике граф — это совокупность непустого множества вершин и множества пар вершин.

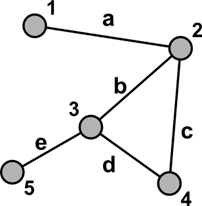
Рисунок 13 Графическое представление простого графа.

Объекты представляются как вершины, или узлы графа, а связи — как дуги, или рёбра. Для разных областей применения виды графов могут различаться направленностью, ограничениями на количество связей и дополнительными данными о вершинах или рёбрах.

Многие структуры, представляющие практический интерес в математике и информатике, могут быть представлены графами.

Граф называется:

· связным, если для любых вершин u,v есть путь из u в v.

· сильно связным или ориентированно связным, если он ориентированный, и из любой вершины в любую другую имеется ориентированный путь.

· деревом, если он связный и не содержит простых циклов.

· полным, если любые его две (различные, если не допускаются петли) вершины соединены ребром.

· двудольным, если его вершины можно разбить на два непересекающихся подмножества V1 и V2 так, что всякое ребро соединяет вершину из V1 с вершиной из V2.

· k-дольным, если его вершины можно разбить на k непересекающихся подмножества V1, V2, …, Vk так, что не будет рёбер, соединяющих вершины одного и того же подмножества.

· полным двудольным, если каждая вершина одного подмножества соединена ребром с каждой вершиной другого подмножества.

· планарным, если граф можно изобразить диаграммой на плоскости без пересечений рёбер.

· взвешенным, если каждому ребру графа поставлено в соответствие некоторое число, называемое весом ребра.

Матрица смежности графа G с конечным числом вершин n (пронумерованных числами от 1 до n) — это квадратная матрица A размера n, в которой значение элемента a_ij равно числу ребёр из i-й вершины графа в j-ю вершину.

Иногда, особенно в случае неориентированного графа, петля (ребро из i-й вершины в саму себя) считается за два ребра, то есть значение диагонального элемента a_ii в этом случае равно удвоенному числу петель вокруг i-й вершины.

Матрица смежности простого графа (не содержащего петель и кратных ребер) является бинарной матрицей и содержит нули на главной диагонали.

Матрица смежности графа, представленного на рисунке 13, выглядит так:

Матрица инцидентности – это прямоугольная матрица размера n на m, где n – число вершин графа, m – число ребер. Матрица инцидентности – бинарная матрица, элемент которой a_ij = 1, если вершина i инцидентна ребру j, то есть ребро j соединяет вершину i с некоей вершиной k, принадлежащей тому же графу. Матрица инцидентности дает выигрыш, когда число ребер относительно мало – порядка количества вершин. Кроме того эта матрица несимметрична. Для графа на рисунке 13 матрица инцидентности выглядит так:

	a	b	c	d	e

При автоматизированных вычислениях чаще используются списки связности. Список связности – это набор вершин графа, каждой из которых в соответствие поставлен список инцидентных ребер. Можно рассматривать список связности как сокращенную запись матрицы инцидентности, из которой убраны все нули. Преимущества такого списка начинают проявляются когда общее количество ребер значительно превышает порядок каждой вершины(число инцидентных ей ребер), что практически всегда соблюдается в графах используемых при проектировании СБИС.

Список связности графа на рисунке 13:

1->a

2->b,c

3->b,d,e

4->c,d

5->e

Представление графа в виде матрицы смежности и инцидентности тривиально:

int mat[N*M];

Обращение к элементам матрицы производится с использованием арифметики индексов:

a_ij = mat[i*M + j];

Стоит отметить, что отсчет строк и столбцов ведется с 0.

Представление в виде списка связности немного сложнее, оно представляет из себя массив, размерностью равный числу вершин, каждый элемент которого содержит указатель на голову списка ребер (мы будем использовать указатели чтобы не ограничивать общности подхода). Каждый элемент этого списка может содержать, например, номер вершины, с которой связывает данную это ребро:

list_ptr g[N];

Чтобы найти, например, связаны ли две вершины ребром, требуется в массиве найти одну из вершин, пройти список ее ребер и проверить есть ли там такое ребро, например для вершин i и j:

list_ptr n = g[i];

while (n!= 0) {

if (n->value == j)

return 1; // Есть такое ребро!

n = n->next;

};

return 0; // Ничего не найдено

По сравнению с матрицей смежности такой способ требует каждый раз проходить список ребер (в худшем случае весь список), но на практике порядок графа практически всегда лежит в пределах 3-5, поэтому эта деградация незначительна. Выигрыш же по потребляемой памяти по сравнению с матрицей смежности достигает порядка (O(n) вместо O(n²)).

Поиск в ширину (BFS, Breadth-first search) – метод обхода и разметки вершин графа.

Поиск в ширину выполняется в следующем порядке: началу обхода s приписывается метка 0, смежным с ней вершинам — метка 1. Затем поочередно рассматривается окружение всех вершин с метками 1, и каждой из входящих в эти окружения вершин приписываем метку 2 и т. д.

Если исходный граф связный, то поиск в ширину пометит все его вершины. Дуги вида (i, i+1) порождают остовный бесконтурный орграф, содержащий в качестве своей части остовное ордерево, называемое поисковым деревом.

Легко увидеть, что с помощью поиска в ширину можно также занумеровать вершины, нумеруя вначале вершины с меткой 1, затем с меткой 2 и т. д.

Для реализации алгоритма нам понадобится функция пометки всех вершин. Для простоты предположим, что пометки вершин хранятся в массиве:

int v[N];

Пусть непомеченные вершины отмечаются -1, тогда функция пометки будет выглядеть так:

int mark(int src, int m) {

list_ptr lp = g[src];

int result = 0;

while(lp!= 0) {

if (v[lp->value] == -1) {

v[lp->value] = m;

result = 1;

} else {

// Эту вершину мы уже посещали!

};

};

return result;

};

Функция возвращает 1 если она пометила хотя бы одну вершину. Теперь займемся обходом графа:

int m = 0;

v[start] = m;

int marked = mark(start, m + 1);

while (marked > 0) {

m++;

marked = 0;

int i = 0;

for (i = 0; i < N; i++) {

if (v[i] == m)

marked += mark (i, m+1);

};

};

Важно отметить, что если граф несвязный, то в результате помеченной останется только та компонента связности, в которой находится стартовая вершина.

Поиск в глубину (англ. Depth-first search, DFS) — один из методов обхода графа. Алгоритм поиска описывается следующим образом: для каждой не пройденной вершины необходимо найти все не пройденные смежные вершины и повторить поиск для них. Используется в качестве подпрограммы в алгоритмах поиска одно- и двусвязных компонент, топологической сортировки.

Для поиска в глубину будем использовать рекурсивный алгоритм. Опишем функцию пометки следующим образом:

int mark(int src, int m) {

if (v[src] == -1)

v[src] = m;

else

return 1;

list_ptr lp = g[src];

while (lp!= 0) {

mark(lp->value, m+1);

lp = lp->next;

};

return 0;

};

Обход графа тогда сводится к вызову функции пометки:

mark (start, 0);

Как мы видим, рекурсивный метод выглядит проще, однако при большой размерности графа рекомендуется применять итерационный метод, поскольку каждый рекурсивный вызов потребляет память на стеке, что может привести к ее исчерпанию.

Алгоритм Дейкстры (Dijkstra’s algorithm) – алгоритм на графах, изобретённый нидерландским ученым Э. Дейкстрой в 1959 году. Находит кратчайшее расстояние от одной из вершин графа до всех остальных. Алгоритм работает только для графов без рёбер отрицательного веса. Алгоритм широко применяется в программировании и технологиях, например, его использует протокол OSPF для устранения кольцевых маршрутов.

Каждой вершине из V сопоставим метку — минимальное известное расстояние от этой вершины до a. Алгоритм работает пошагово — на каждом шаге он «посещает» одну вершину и пытается уменьшать метки. Работа алгоритма завершается, когда все вершины посещены.

Инициализация. Метка самой вершины a полагается равной 0, метки остальных вершин — бесконечности. Это отражает то, что расстояния от a до других вершин пока неизвестны. Все вершины графа помечаются как непосещённые.

Шаг алгоритма. Если все вершины посещены, алгоритм завершается. В противном случае, из ещё не посещённых вершин выбирается вершина u, имеющая минимальную метку. Мы рассматриваем всевозможные маршруты, в которых u является предпоследним пунктом. Вершины, в которые ведут рёбра из u, назовем соседями этой вершины. Для каждого соседа вершины u, кроме отмеченных как посещённые, рассмотрим новую длину пути, равную сумме значений текущей метки u и длины ребра, соединяющего u с этим соседом. Если полученное значение длины меньше значения метки соседа, заменим значение метки полученным значением длины. Рассмотрев всех соседей, пометим вершину u как посещенную и повторим шаг алгоритма.

Рассмотрим реализацию алгоритма на языке Си. Для этого представим что ребра в списке связности представлены в виде структуры:

list_node {

int target_vertex;

int cost;

};

Обозначим так же указатель на элемент списка:

typedef list_node* list_ptr;

Опишем функцию, котрая проверяет, смежны ли вершины и возвращает стоимость ребра, если смежны:

int edge (int i, in j) {

list_ptr = g[i];

while (list_ptr!= 0) {

if (list_ptr->vertex == j)

return list_ptr->cost;

};

return -1;

};

Введем массив вычисляемых расстояний от заданной верщины и массив родителей, который представляет собой путь из исходной вершины в виде набора связных списков на массиве:

int dist[N];

int parent[N];

Обозначим start начальную вершину, из которой и будем искать пути. Так же заведем массив уже посещенных вершин:

int in_tree[N] = {0};

Заполним массив расстояний бесконечностью:

for(int i = 0; i < N; i++)

dist[i] = INT_MAX;

Начинаем со стартовой вершины:

dist[start] = 0;

int cur = start;

Пока есть необработанные вершины:

while(!in_tree[cur]) {

in_tree[cur] = 1;

for(int i = 0; i < N; i++) {

int cost = edge(cur, i);

if(cost > 0) {

int d = dist[cur] + cost;

if(d < dist[i]) {

dist[i] = d;

parent[i] = cur;

};

};

};

Теперь найдем нерассмотренную вершину с минимальным расстоянием:

int min_dist = INT_MAX;

for(int i = 0; i < N; i++) {

if(!in_tree[i] && dist[i] < min_dist) {

cur = i;

min_dist = dist[i];

};

};

};

Задача коммивояжёра (англ. Travelling salesman problem, TSP) (коммивояжёр – разъездной сбытовой посредник) - одна из самых известных задач комбинаторной оптимизации, заключающаяся в отыскании самого выгодного маршрута, проходящего через указанные города хотя бы по одному разу с последующим возвратом в исходный город. В условиях задачи указываются критерий выгодности маршрута (кратчайший, самый дешёвый, совокупный критерий и т. п.) и соответствующие матрицы расстояний, стоимости и т. п. Как правило, указывается, что маршрут должен проходить через каждый город только один раз — в таком случае выбор осуществляется среди гамильтоновых циклов.

Существует несколько частных случаев общей постановки задачи, в частности геометрическая задача коммивояжёра (также называемая планарной или евклидовой, когда матрица расстояний отражает расстояния между точками на плоскости), треугольная задача коммивояжёра (когда на матрице стоимостей выполняется неравенство треугольника), симметричная и асимметричная задачи коммивояжёра. Также существует обобщение задачи, так называемая обобщённая задача коммивояжёра.

Общая постановка задачи, впрочем как и большинство её частных случаев, относится к классу NP-полных задач.

Практический пример:

При бессеточной трассировке межсоединений вводится так называемый граф путей.

Рисунок 14 Граф путей.

Такой граф показывает трассировщику, какие области можно соединить с помощью проводников. Для того чтобы провести проводник требуется найти путь от одного терминала до второго, используя граф путей. Если в качестве веса ребер использовать расстояние между узлами графа или другие критерии трассировки, то с помощью алгоритма Дейкстры мы можем найти минимизирующее эти критерии положение трассы.

Вопросы и задания для самостоятельной проработки:

1. Переделайте реализацию поиска в ширину с использованием рекурсии.[2]

2. Переделайте реализацию поиска в глубину с использованием итераций.[3]

3. Адаптируйте алгоритм Дейкстры к использованию массивов и матрицы смежности вместо списка связности.[5]

4. Реализуйте структуру данных, представляющую граф. Ребра и вершины представьте отдельными структурами.[1, с.453]

Список литературы:

1. Кормен, Т., и другие, Алгоритмы: построение и анализ.

2. Ананий В. Левитин Глава 5. Метод уменьшения размера задачи: Поиск в ширину.

3. Ананий В. Левитин Глава 5. Метод уменьшения размера задачи: Поиск в глубину

4. http://faqs.org.ru/progr/graph/pathmake.htm

5. http://iu9.wikidot.com/dijkstra

Лекция 7 Задача декомпозиции. Критерии декомпозиции. Представление схемы в виде графа. Подходы к декомпозиции. Кластеризация. Бисекция. Алгоритм Кодреса. Алгоритм Кернигана-Лина.

Содержание:

1. Декомпозиция.

2. Критерии декомпозиции.

3. Кластеризация и бисекция.

4. Алгоритм Кодреса.

5. Алгоритм Кернигана-Лина.

Декомпозиция — научный метод, использующий структуру задачи и позволяющий заменить решение одной большой задачи решением серии меньших задач.

Применительно к проблеме проектирования СБИС, декомпозицией называется разбиение электрической схемы СБИС на множество иерархических блоков. Такое разбиение необходимо ввиду того что задачи, решаемые при проектирования СБИС имеют слишком высокую сложность. Кроме того, декомпозиция позволяет оптимизацию по критериям, оценка которых недоступна на следующих этапах проектирования.

Наиболее часто используемым критерием декомпозиции является количество связей между блоками, поэтому если представить элементы схемы в виде вершин графа, а связи между элементами в виде ребер, то задача декомпозиции сводится к нахождению такого множества подграфов размера не более N, полностью покрывающих исходный граф, так чтобы было минимально число инцидентных друг другу вершин, входящих в различные подграфы.

Другими критериями декомпозиции, особенно в современных СБИС являются одинаковые напряжения питания, принадлежность к единым тактируемым блокам. Вместе группируют так же элементы из одинаковых библиотек и близкие по функциональному назначению.

Рисунок 15 Пример функциональной декомпозиции.

Наиболее распространены два подхода к декомпозиции графа – кластеризация и бисекция.

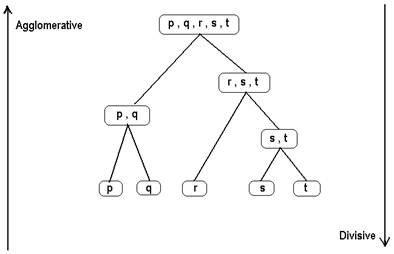
Рисунок 16 Два подхода к декомпозиции - кластеризаци (agglomerative) и (би)секция (divisive)

Суть подхода кластеризации состоит в поиске «центров кристаллизации» - вершин графа, которые служат «затравками» для будущих подграфов. На каждом шаге алгоритма кластеризации к «затравкам» присоединяется одна либо несколько инцидентных вершин, отобранных по определенному критерию. В алгоритме Кодреса например таким критерием служит сильная связность (большое число связей) с вершинами данной группы и слабая связность (малое число связей) с остальными вершинами графа.

После того как для всех вершин графа схемы определен подграф в который они входят, действие алгоритма заканчивается. Далее, если результат не устраивает проектировщика, возможен повторный запуск, с изменением «затравок», либо критериев отбора инцидентных вершин, либо комбинацией того и другого.

Метод бисекции на каждом шаге разбивает граф на два подграфа, которые затем рекурсивно проходят ту же процедуру. Алгоритм бисекци

Дата добавления: 2014-01-07