Количественные критерии оценки тесноты связи

Величина коэффициента корреляции	Характер связи
до ±0,3	практически отсутствует
±0,3 - ±0,5	слабая
±0,5 - ±0,7	умеренная
±0,7 - ±1,0	сильная

По направлению выделяют связь прямую и обратную. Прямая - это такая связь, при которой с увеличением или с уменьшением значе­ний факторного признака происходит увеличение или уменьшение зна­чений результативного. Так, например, рост производительности труда способствует увеличению уровня рентабельности производства. В слу­чае обратной связи значения результативного признака изменяются под воздействием факторного, но в противоположном направлении по сравнению с изменением факторного признака. Так с увеличением уровня фондоотдачи снижается себестоимость единицы производимой продук­ции.

По аналитическому выражению выделяют связи прямолинейные (или просто линейные) и нелинейные. Если статистическая связь меж­ду явлениями может быть приблизительно выражена уравнением пря­мой линии, то ее называют линейной связью вида:

(9.1.)

Если же связь может быть выражена уравнением какой – либо кривой линии, например:

Параболы - 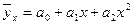(9.2.)

Гиперболы - 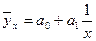; и т.д., то какую связь называют нелинейной или криволинейной. Для выявления наличия связи, ее характера и направления в статистике используются методы: приведения параллельных данных; аналитических группировок; графический; корреляции.

Метод приведения параллельных данных основан на сопоставлении двух или нескольких рядов статистических величин. Такое сопоставление позволяет установить наличие связи и получить представление о ее характере. Сравним изменение двух величин:

X
Y

Мы видим, что с увеличением величины X величина Y также возрастает. Можно сделать предположение, что связь между ними прямая и что ее можно описать или уравнением прямой или уравнением параболы второго порядка.

Графически взаимосвязь двух признаков изображается с помо­щью поля корреляции. В системе координат на оси абсцисс откладыва­ются значения факторного признака, а на оси ординат - результативного. Каждое пересечение линий, проводимых через эти оси, обозначаются точкой. При отсутствии тесных связей имеет место беспорядочное рас­положение точек на графике. Чем сильнее связь между признаками, тем теснее будут группироваться точки вокруг определенной линии, выражающей форму связи.

Y

0 X

Рис. 9.1. График корреляционного поля.

Корреляция - это статистическая зависимость между случайными величинами, не имеющая строго функционального характера, при кото­рой изменение одной из случайных величин приводит к изменению ма­тематического ожидания другой.

В статистике принято различать следующие варианты зависимо­стей:

1.Парная корреляция - связь между двумя признаками (результативным и факторным, или двумя факторными).

2.Частная корреляция - зависимость между результативным и одним факторным признаками при фиксированном значении других фактор­ных признаков.

3.Множественная корреляция - зависимость результативного и двух или более факторных признаков, включенных в исследование.

Корреляционный анализ имеет своей задачей количественное определение тесноты связи между двумя признаками (при парной связи) и между результативным и множеством факторных признаков (при мно­гофакторной связи).

Теснота связи количественно выражается величиной коэффициен­тов корреляции, которые, давая количественную характеристику тесноты связи между признаками, позволяют определять «полезность» фактор­ных признаков при построении уравнения множественной регрессии.

Регрессия тесно связана с корреляцией: первая оценивает силу (тесноту) статистической связи, вторая исследует ее форму.

Регрессионный анализ заключается в определении аналитиче­ского выражения связи, в котором изменение одной величины (называе­мой зависимой или результативным признаком), обусловлено влиянием одной или нескольких независимых величин (факторов).

Одной из проблем построения уравнений регрессии является их размерность, то есть определение числа факторных признаков, вклю­чаемых в модель. Их число должно быть оптимальным.

Сокращение размерности за счет исключения второстепенных, несущественных факторов позволяет получить модель, быстрее и качественнее реализуемую. В то же время, построение модели малой размерности может привести к тому, что она будет недостаточно полно описы­вать исследуемое явление или процесс.

При построении моделей регрессии должны соблюдаться следую­щие требования:

1.Совокупность исследуемых исходных данных должна быть од­нородной и математически описываться непрерывными функциями.

2.Возможность описания моделируемого явления одним или несколькими уравнениями причинно-следственных связей.

3.Все факторные признаки должны иметь количественное (циф­ровое) выражение.

4.Наличие достаточно большого объема исследуемой выборочной совокупности.

5.Причинно-следственные связи между явлениями и процессами должны описываться линейной или приводимой к линейной форме зави­симостью.

6.Отсутствие количественных ограничений на параметры модели связи.

7.Постоянство территориальной и временной структуры изучае­мой совокупности.

Соблюдение данных требований позволяет построить модель, наилучшим образом описывающую реальные явления и процессы.

Дата добавления: 2014-01-07