Проективные преобразования

Пусть в n-мерном проективном пространстве RPⁿ наряду с однородной системой координат {Е₁,Е₂,...,E_n+1,E}=R задана новая проективная система координат {Е'₁,Е'₂,...,Е'_n+1,E'}=R' и произвольная точка МRPⁿ имеет в системе R координаты х₁,х₂,...,х_n+1.

Опр.1. Преобразование f пространства RPⁿ называется проективным, если каждой точке МRPⁿ ставится в соответствие точка М'RPⁿ, имеющая в новой системе координат R' те же самые координаты, которые точка М имела в исходной системе координат R:

.

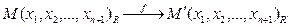Замечание 1. Аналогично определяется и проективное отображение одного проективного пространства на другое (той же размерности).

Замечание 2. Из определения 1 непосредственно следует что преобразование f^-1 проективного пространства RPⁿ, обратное к проективному преобразованию f, также есть проективное преобразование. Очевидно также, что тождественное преобразование е проективного пространства есть его проективное преобразование.

Если новая система координат R' задана невырожденной квадратной матрицей С=(с_ij) порядка n+1, то из формул (2) преобразования координат §26 следует, что точка будет иметь в старой системе координат R следующие координаты (однородные):

, (1)

где 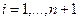, , 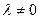det(c_ij) .

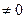Замечание 3. Проективное преобразование можно определить и как преобразование, ставящее в соответствие каждой точке 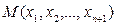арифметического проективного пространства точку М', однородные координаты которой даны формулами (1) при условии det(c_ij)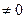, причём система координат всегда одна и та же. Поэтому проективное преобразование пространства RPⁿ полностью определяется заданием невырожденной квадратной матрицы n+1 -го порядка.

Замечание 4. Если проективные преобразования f₁ и f₂ задаются соответственно матрицами А и В, то произведение этих матриц А и В задаёт композицию f₁ и f₂. Значит, композиция двух проективных преобразований является проективным преобразованием. Учитывая замечание 2, имеем основной факт.

Теорема 1. Проективные преобразования проективного пространства RPⁿ образуют группу, являющуюся подгруппой в группе всех преобразований этого пространства.

Теорема 2. Проективные преобразования f пространства RPⁿ отображает любую r-мерную плоскость на плоскость 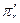той же размерности r.

Доказательство.

Пусть плоскость задана в проективной системе координат R системой из n-r линейно независимых однородных уравнений вида:

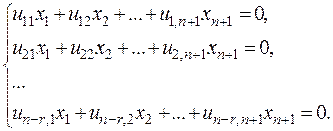(2)

Обозначим 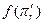и образы плоскости и системы координат R при данном проективном преобразовании f. Так как проективное преобразование вполне определяется заданием пары проективных систем координат R и R', то R'=f(R) также проективная система координат. Согласно определению, координаты образов точек в системе координат R' и координаты их прообразов в системе координат R совпадают, тогда фигура 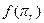относительно системы координат R' задаётся такими же уравнениями (2), что и плоскость в системе координат R. Значит - плоскость размерности r.

Теорема доказана.

§ 29. Квадрики в проективном пространстве и их проективная классификация.

Опр.1. Квадрикой или гиперповерхностью второго порядка в n-мерном проективном пространстве RPⁿ называется множество точек, координаты которых относительно какой-нибудь проективной системы координат R удовлетворяют уравнению 2-ой степени вида:

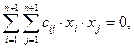(1)

где c_ij=c_ji.

Замечание 1. При переходе к другой проективной системе координат R' квадратичная форма из левой части уравнения (1) подвергается однородному линейному преобразованию переменных с невырожденной матрицей и переходит в квадратичную форму от новых переменных . Поэтому степень уравнения (1) остаётся равной двум, т.е. понятие квадрики не зависит от выбора проективной системы координат.

Пусть проективное пространство RPⁿ есть результат пополнения несобственными или бесконечно удалёнными точками n-мерного аффинного пространства А_n. Выберем в пространстве А_n аффинную систему координат , которая порождает фиксированную однородную систему координат 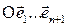пространства А_n+1 где и . Будем также считать, что уравнения квадрик пространства RPⁿ = 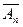заданы именно в однородной системе координат.

Имеет место теорема единственности: Если два уравнения вида (1) определяют одну и ту же квадрику в пространстве RPⁿ=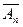, то коэффициенты в обоих этих уравнениях соответственно пропорциональны.

Известно, что с помощью линейного преобразования переменных любая квадратичная форма 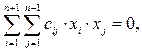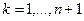, det(a_kj) 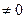может быть приведена к каноническому и даже нормальному виду (см. § 18):

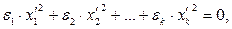(2) где - ранг квадратичной формы (число ненулевых коэффициентов при квадратах новых переменных), а все числа 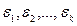равны .

Дата добавления: 2014-01-07