Основные свойства кривой Гаусса

1. 
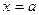2. ось симметрии
3. при
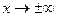
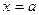4. точка max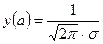
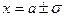5. точки перегиба

σ = 3

σ = 1

σ = 8

При увеличении σ уменьшается амплитуда, и график становится более пологим

2. Основные характеристики нормального распределения

3. Вероятность попадания нормально распределенной случайной величины на заданный отрезок

4. Отклонение нормально распределенной случайной величины от её математического ожидания

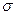
	0.6826
2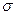	0.9544
3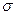	0.9973
4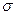	0.9994

Правило трех сигм:

Если случайная величина распределена нормально, то считается практически невозможным ее отклонение от Мбольше, чем на 3.

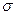Более того, на практике, если некоторая случайная величина отклоняется от своего среднего значения меньше чем на 3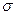, то есть основание предполагать, что эта случайная величина нормально распределенная.

5. Расчет доверительных интервалов

Считается, что параметры нормального распределения известны и заданна вероятность отклонения случайной величины от М, в которую случайная величина попадает с вероятность .

Пример:

Найти интервал, попадание в который, осуществляется с вероятностью =0.95

0.95 = 2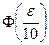

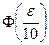= 0.475

= 1.96

Некоторые важнейшие распределения связанные с нормальным.

I) - распределение.

- случайная величина, нормально распределенная с параметрами (0: 1), тогда случайная величинаимеет следующую плотность распределения:

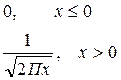
Пусть, 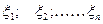- совокупность n независимых нормально распределенных случайных величин с параметрами (0;1), тогда случайная величина = обладает распределением, которое принято называть - распределением с n степенями свободы.

Свойства - распределния:

1. Плотность - распределения.

=

Гамма функция.

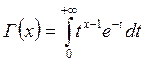
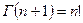
Плотность - распределения исключительно зависит от степеней свободы к.

2.

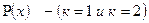являются монотонно убывающими.

При к = 3: х = к -2 есть локальный максимум.

3.

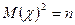
4. С увеличением к – числа степеней свободы - распределение медленно приближается к нормальному.

II) Распределение Стьюдента (t – распределение)

Пусть случайные величины 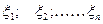нормально распределены с параметрами , тогда случайная величина 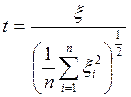имеет распределение, которое называется t – распределением или распределением Стьюдента с n – степенями свободы.

1) Р(х) = - четная функция

2) По мере увеличения n, распределение Стьюдента быстро приближается к нормальному.

III) Распределение Фишера-Снедекора (F – распределение).

Пусть и нормально распределены с параметрами (0; 1). Распределение случайной величины вида:

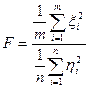называется распределением со степенями свободы т и п.

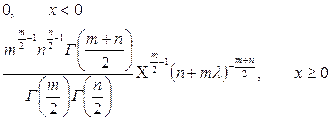
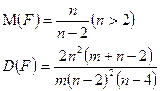
Закон больших чисел.

При некоторых, достаточно общих, условиях, суммарное поведение большого числа случайных величин почти утрачивает случайный характер и становится закономерным. Для практики важно знание условий, при выполнении которых совокупное действие многих случайных величин приводит к результату почти независящему от случая. Эти условия и составляют суть законов больших чисел.

Теорема Чебышева.

Пусть попарно независимые случайные величины, имеющие

и 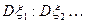. Пусть также дисперсии всех случайных величин ограниченны некоторой константой, т.е. 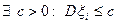, тогда 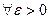выполняется следующее соотношение:

Доказательство:

Воспользуемся вторым неравенством Чебышева.

Пусть ; ;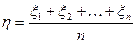

; ;

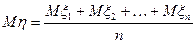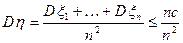Смысл закона больших чисел заключается в том, что при больших n, с вероятностью близкой к 1, среднее арифметическое суммы независимых случайных величин становится близким к const, равной среднему арифметическому математических ожиданий этих случайных величин.

Следствие теоремы Чебышева: Если при условиях теоремы Чебышева 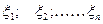имеют равные между собой математические ожидания 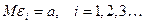, то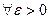

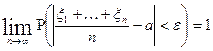
Следствие теоремы Чебышева обосновывает принцип среднего арифметического, используемого во всех экспериментальных дисциплинах, т.е. если производится серия n – измерений без систематической ошибки, то среднее арифметическое результатов наблюдается при больших n сколько угодно мало отличается от измеряемой величины.

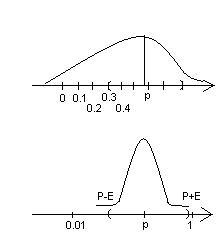
Теорема Бернулли.

Пусть m – число успехов в серии n испытаний в схеме Бернулли с вероятностью p – успехов в каждом испытании. 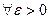выполняется следующее предельное соотношение:

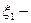число успехов в первом эксперименте.

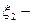во втором.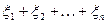

Число успехов в данной серии испытаний

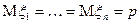
Сходимость величин ;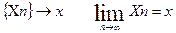

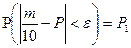
Центральная предельная теорема.

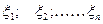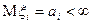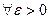Если случайные величины - независимы, нормально распределены с конечными математическими ожиданиями , конечные дисперсии , тогда выполняется:

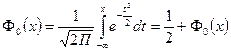
Теорема Ляпунова.

Если 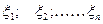- независимы, имеют конечные математические ожидания 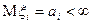, конечные дисперсии

;

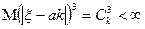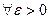
выполняется следующее соотношение:

Как следует из теоремы Ляпунова: совокупное действие случайных величин различной природы оказывается близким к нормальному распределению.

Потоки событий.

Поток событий – последовательность событий, которые наступают в случайные моменты времени.

Свойства потоков:

1. Стационарность потока.

Поток называется стационарным, если вероятность появления ровно m- событий на промежутке времени длительностью 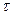зависит только m и 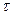, и не зависит от момента времени, в который этот временной промежуток начался.

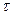
2. Отсутствие последствия.

Говорят, что поток обладает свойством отсутствия последствия, если вероятность появления m- событий на любом промежутке времени не зависит от того, появились или нет события в момент времени непосредственно предшествующий началу рассматриваемого промежутка.

Предыстория потока не сказывается на вероятности появления событий в будущем.

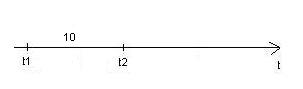
Если поток обладает таким свойством, то выполняется взаимная независимость числа событий в непересекающихся промежутках времени.

3. Ординарность потока.

Говорят, что поток обладает свойством ординарности, если за бесконечно малые промежутки времени может произойти не более одного события в потоке, т.е. появление 2-х и более событий практически невозможно.

4. Простейший (Пуассоновский) поток.

Простейшим потоком называется поток, который обладает всеми тремя свойствами.

Теорема: Если поток представляет собой сумму большого числа независимых стационарных потоков, влияние каждого на сумму ничтожно мало, то ординарный поток при условии его ординарности является простейшим.

Определение: Интенсивность потока называется среднее число событий происходящих за единицу времени.

- интенсивность

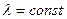
m – событий за промежуток времени

; ;

Замена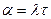

Простейший поток должен обладать 3-мя свойствами:

1. Стационарность.
2. Отсутствие последствия.
3. Ординарность.

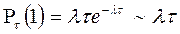
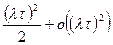
Пример: На телефонную станцию поступают 2 вызова в 1 минуту. Какова вероятность, что за 5 минут наступит 12 звонков.

Дано:

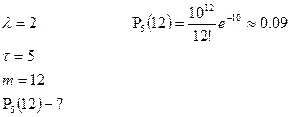
Введение в теорию цепей Маркова.

Цепь Маркова – последовательность испытаний, в каждом из которых, появляется и при том только один из несовместных событий . При этом условная вероятность того, что в испытании с номером S наступит событие при условии, что в S-1 испытании было не зависит от результатов предшествующих испытаний.

События называются состояниями системы, а сами испытания называются изменениями состояний системы.

Если изменение состояний происходит в фиксированные моменты времени, то такая цепь называется цепью Маркова с дискретными временами.

Если изменение состояний происходит в произвольные моменты времени, то цепь Маркова называют цепью с непрерывным временем.

Цепь Маркова называется однородной, если условная вероятность перехода из состояния в состояние не зависит от номера испытания S.

№1 №2 №3 №S-1 №S №S+1

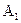
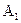
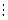
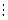
Для однородных цепей Маркова 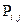называются переходными вероятностями.

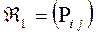
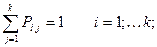
Равенство Маркова.

- вероятность перехода из состояния в ; за n испытаний.

m n-m

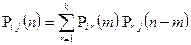
1) n = 2; m=1;

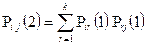
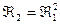
2) n = 3; m = 1;

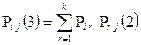
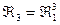
3)

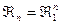
Пример:

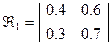
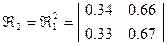
Производные функции.

Определение: Дискретная случайная величина называется целочисленной, если она принимает только целые неотрицательные значения 0; 1; 2;с соответствующими вероятностями.

Определение: Производящей функцией целочисленной случайной величины называется функция вида: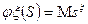

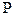
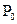
- разложение функции в ряд Макларена

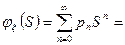
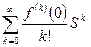
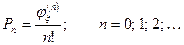
1. Биноминальное распределение.

Количество испытаний n с вероятностью успеха p, неуспеха q.

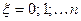
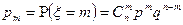
2. Распределение Пуассона.

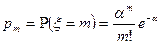
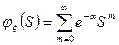
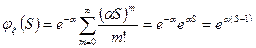
3. Геометрическое распределение.

Факториальным моментом порядка к случайной величины называется:

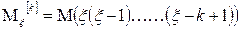
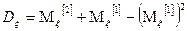
Теорема:

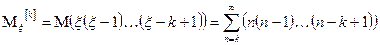
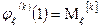
1. Биноминальное распределение.

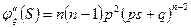
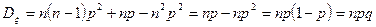
2. Распределение Пуассона.

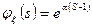
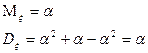
3. Геометрическое распределение.

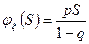
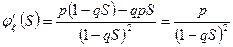
Теорема о мультипликативном свойстве производящих функций.

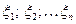- независимые целочисленные случайные величины, имеющие производящие функции , то

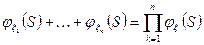
Доказательство:

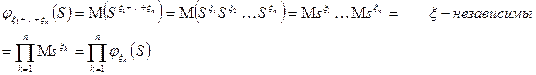
Пример: 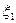- биноминальное распределение случайной величины

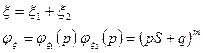
Характеристические функции.

Пусть действительные случайные величины с конечными 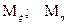, тогда случайная величина 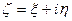называется комплексной случайной величиной, имеющей математическое ожидание .

Все основные свойства математических ожиданий переносятся и на случай комплексных случайных величин.

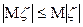
Определение: Характеристической функцией случайной величины называется функция

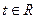
Если известна функция распределения или 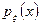, то явная запись будет

В случае дискретных случайных величин

Свойства характеристической функции:

1)

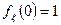
2) Характеристическая функция равномерно непрерывна по аргументу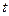

3) Если случайные величины связаны минимальным соотношением ,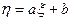

где 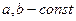, то

Доказательство:

4)

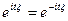
5) Мультипликативное свойство характеристической функции.

Если случайные величины 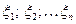- независимы, то

Доказательство:

6) Пусть , тогда характеристическая функция дифференцируема до порядка n включительно, выполняется следующее соотношение

Доказательство:

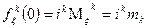
7)Если дискретная целочисленная случайная величина, то ее характеристическая и производящая функции связанны следующей формулой:

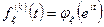
Примеры характеристических функций.

1. Биноминальное распределение. n – экспериментов, р – вероятность успеха.

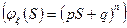
2. Распределение Пуассона.

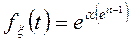
3. Геометрическое распределение.

4.

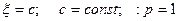
5. Нормальное распределение.

а) Нормальное распределение (0; 1)

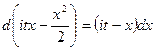
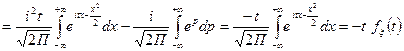
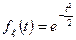
б) Произвольное нормальное распределение

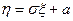, если - нормально распределенная случайная величина с параметрами (0;1),

- нормально распределенная случайная величина с параметрами

Замечание о сумме нормальных распределений:

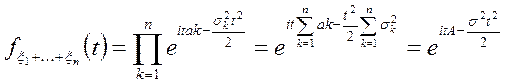
Сумма нормальных распределений есть нормальное распределение случайных величин.

6. Равномерное распределение на отрезке

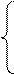
Если рассматривается симметрический отрезок [- l;l ]

Теорема: Любой характеристической функции соответствует и при том единственная функция распределения (плотность распределения).

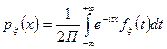
Дата добавления: 2014-01-07