ЛЕКЦИЯ 6. Часто. встречается другая задача: известна статистическая модель и надо найти характеристики надежности системы

Часто. встречается другая задача: известна статистическая модель и надо найти характеристики надежности системы, т. е. характеристики распределения наработки.до отказа и других, случайных величин, определяющих надежность изделия. Известно большое число таких характеристик. Например, плотность распределения f(х) — это функция, которая должна удовлетворять двум условиям;

f(х)=0; 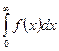=1

Можно найти различные функции, принимающие неотрицательные значения, интеграл которых равен единице в заданной области изменения. Наиболее желательно строить статистическую модель и выбирать плотность распределения с учетом характера рассматриваемых явлений и имеющихся экспериментальных данных.

Исходными данными для определения распределения является обычно эмпирическая плотность распределения, т. е. наблюдаемые значения случайной величины, сгруппированные по частоте появления. По опытным данным строится гистограмма или график плотности распределения. Обработка гистограммы позволяет перейти от эмпирического распределения к той или иной статистической модели, подобрать то или иное распределение. Для таких расчетов удобно пользоваться ЭВМ.

Рассмотрим распределения, наиболее часто встречающиеся при исследованиях надежности автомобилей.

Экспоненциальное распределение служит распространенной моделью для времени безотказной работы. Оно предполагает, что события (отказы) происходят независимо одно от другого с постоянной интенсивностью и поэтому удобно для описания несистематических отказов.

В распределении времени безотказной работы изделия можно найти такие периоды (обычно при нормальной эксплуатации), для которых экспоненциальное распределение справедливо. На пример, распределение безотказной работы двигателя за весь срок существенно отличается от экспоненциального, но если двигатель установлен после приработки и заменен к моменту начала износных отказов другим, тоже прошедшим приработку, распределение его отказов часто можно считать экспоненциальным.

Можно показать, что экспоненциальное распределение «в пределе» является статистической моделью времени безотказной работы системы с большим числом последовательно соединенных элементов. При этом распределение времени безотказной работы отдельных элементов может не быть экспоненциалиным, важно только, чтобы каждый элемент в отдельности не оказывал очень большого влияния на вероятность выхода из строй всей системы. Поэтому эксвоненциальное распределение часто успешно описывает распределение времени безотказной работы систем, в которых каждый откаэавший элемент немедленно заменяется работоспособным.

Плотность распределения отказов имеет вид

f(х,λ) = λexp(- λx) при х ≥ 0, λ ≥ 0 (0 в остальных случаях).

Экспоненциальное распределение является однопараметрическим, т. е. зависит от одного параметра х. Интегральная функция распределения отказов

F(х, λ) = = 1— ехр(—λ х).

Функция безотказной работы

R(х, λ) = 1—F(х, λ) = ехр(—λх).

Интенсивность отказов можно найти, воспользовавшись фор мулой (4):

Таким образом, параметр λ — это интенсивность отказов. Постоянство этого параметра означает, что вероятность отказа элемента предполагается не зависящей от его предыстории: прокол шины в равной степени вероятен после проезда 5 или 10 тыс. км. Допущение о том, что нет износа, накопления усталостного разрушения, старения, — вообще серьезное допущение;

Если имеется наработка х₀ в течение которой отказы не на ступают, то

f(х, λ, х₀) = λ exp[ - λ(x –x₀)] при х ≥ x₀,, λ ≥ 0 (0 в остальных случаях).

Средняя наработка (математическое ожидание) до отказа х_ср = 1/ λ. Гамма-процентный ресурс Р (х_γ) = ехр (—λх_γ) = 0,01γ.

Логарифмируя, получим - λх_γ = Iп 0,01 γ, откуда х_γ = - (ln 0,01 γ)/ λ = х_ср(—Iп 0,01 γ).

Н ор м а л ь н о е (и л и г а у с с о в о) р а с п р е д е л е н и е является наиболее часто используемой статистической моделью, что может быть объяснено теоретически и подтверждено экспериментальными данными. Теоретическим обоснованием нормального распределения является центральная предельная теорема. Смысл ее состоит в том, что закон раслределения случайной величины, представляющей собой общий результат большого числа независимых небольщих воздействий, будет тем ближе к нормальному, чем больше число наблюдений. Этот результат справедлив независимо от того, по какому закону распределена каждая из случайных величин, средняя из которых рассматривается.

Плотность нормального распределения имеет вид

при 0 < х < ∞; 0 < m_х < ∞; σ > 0

где m_х — среднее значение или математическое ожидание (параметр, характеризующий центр распределения), σ —среднее квадратическое отклонение случайной величины х (параметр, характеризующий масштаб распределения). Поэтому

х_ср = m_х

Интегральная функция нормального распределения отказов

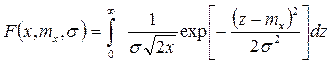
Для функции безотказной работы имеем

где — табулированная функция.

Наработка до отказа не может быть отрицательной, и поэтому приведенные выражения справедливы только при достаточно малых средних квадратических отклонениях, когда σ < m_х/3 или коэффициент вариации ν = σ / m_х < ⅓- Это следует из особенности случайных величин, имеющих нормальное распределение — 99,7 % эначений случайной величины заключено в интервале m_х±3σ Отсюда возникает «правило трех σ» — практически все значения случайной величины лежат в интервале ±3σ. Действительно, шанс на то, что выбранная случайным образом нормально распределенная случайная величина окажется в этом интервале, составляет 997 из 1000.

Логарифмически-нормальное распределение (логнормальное) позволяет описать самые различные случайные величины и может быть принято в качестве распределения времени безотказной работы как на теоретической, так и на экспериментальной основе, когда случайная величина получается в результате перемножения большого числа небольших погрешностей, подобно тому как нормальное распределение имеет место при сложении погрешностей.

Из свойств логнормального распределения можно полагать, что оно более применимо для оценки степени износа к определенному времени или при испытаниях на долговечность.

В Случае логнормального распределения логарифм случайной величины распределен по нормальному закону.

Если z = ln х, то плотность распределения будет

при х>0; - ∞ < m_х < ∞; σ > 0; 0 в остальных случаях.

В том случае, когда отказы появляются только после некоторого значения х₀ плотность распределения определяется следующим образом:

при х ≥ х₀; σ > 0

В этих формулах m_х и σ уже не являются параметрами, характеризующими центр распределения и его масштаб. Сами функции распределения имеют правостороннюю асимметрию, тем большую, чем больше σ.

Распределение Вейбулла соответствует более общей статистической модели, чем предыдущие распределения, охватывая различные законы изменения случайной величины с течением времени.

Плотность распределения

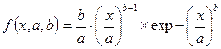
при а > 0; х ≥ 0, b > 0; (0 в остальных случаях)

Распределение Вейбулла — двухпараметрическое, параметр а называют иногда параметром масштаба, а параметр b — параметром формы. Интегральная функцй распределения отказов

= 1 — ехр [ - (х/а)^b] при х>0.

Если имеется наработка х₀ в течение которой отказы не наступают, т. е. при произвольном начале отсчета, имеем

при х ≥ х₀; - ∞ < х < ∞; а > 0; b > 0 (0 в остальных случаях).

Функция безотказной работы

R(х, а, b, х₀) = при х≥0.

Интенсивность отказов

λ(х) =

Средняя наработка до отказа

х_ср = аГ(1 – 1/b)

где Г — гамма - функция (по справочным данным).

Гамма – процентный ресурс определяется по формуле

100exp[ - (x_γ/a)^b] = γ.

Логарифмируя, получим (х_γ /а)^b = — ln (γ /100), откуда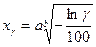

На рис. 6 показано, как меняется плотность распределения при различных значениях параметра b формы.

Рис. 6. Плотность распределения Вейбулла при различных зиаченаях параметра b формы:

а — обычная координатная сетка; б — специальная

Распределение Вейбулла является достаточно универсальным, охватывающим разнообразные случаи изменения вероятности отказов. В частности:

при b < 1 плотность распределения имеет вид убывающей функции — интенсивность отказов убывает с наработкой;

при b = 1 распределение Вейбулла совпадает с экспоненциальным, а интенсивность отказов постоянна λ= 1/а;

при b > 1 плотность распределения одновершинн а λ(х) возрастает с течением времени;

при b = 2 интенсивность отказов является линейной функцией (этот частный случай распределения Вейбулла совпадает с так называемым распределением Рэлея);

при b =3,3...3,5 распределение Вейбулла весьма близко к нормальному закону распределения.

Коэффициент формы b характеризует рассеяние случайной величины. Ниже приведены данные его связи с коэффициентом вариации.

b 0.5 1,0 1,5 2,0 2,5 3,0 3,5

ν 2,24 1,0 0,68 0,52 0,43 0,365 0,316

Дата добавления: 2014-01-07