Ограниченные подмножества множества R

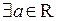Определение 1. Множество называется ограниченным сверху, если такое, что . В этом случае число называется мажорантой множества A.

Пример. Множество точек полубесконечного интервала обладает мажорантой (например, 6).

Определение 2. Множество называется ограниченным снизу, если такое, что . В этом случае число называется минорантой множества A.

Пример. У множества из предыдущего примера нет минорант, поэтому оно не ограничено снизу.

Определение 3. Множество, ограниченное и сверху, и снизу, называется ограниченным.

Определение 4. Пусть множество ограничено сверху. Если такое, что , то называется максимальным элементом множества A.

Очевидно, что максимальный элемент является мажорантой. Если максимальный элемент множества существует, то он единственен (докажите самостоятельно).

Пример. Множество точек полубесконечного интервала не имеет максимального элемента, а множество точек имеет максимальный элемент 3.

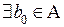Определение 5. Пусть множество ограничено снизу. Если такое, что , то называется минимальным элементом множества A.

Очевидно, что минимальный элемент является минорантой. Если минимальный элемент множества существует, то он единственен (докажите самостоятельно).

Утверждение 1. Если множество A ограничено сверху, то существует, причем единственный, минимальный элемент на множестве мажорант, называемый супремумом множества A (обозначается sup A).

Доказательство. Рассмотрим множество B всевозможных мажорант множества A. Для и 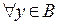справедливо: 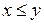. Согласно аксиоме непрерывности такое, что для и 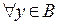. Согласно определению 1 является мажорантой A, следовательно, . Согласно определению 3 является минимальным элементом на множестве мажорант. Следовательно, . Единственность супремума следует из единственности минимального элемента.

Утверждение 1-а. Если множество A ограничено снизу, то существует, причем единственный, максимальный элемент на множестве минорант, называемый инфимумом множества A (обозначается inf A).

Утверждение 2. Пусть 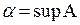. Тогда для тчо .

Доказательство. От противного. Пусть тчо (). Следовательно, является мажорантой множества A, и значит, , будучи больше , не является минимальным элементом на множестве мажорант, то есть . Пришли к противоречию.

Утверждение 2-а. Пусть 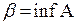. Тогда для тчо .

Дата добавления: 2014-01-07