Решение. Модуль 3. Модульные единицы 16,17

Модуль 3. Модульные единицы 16,17

Занятие 13 Однофакторный дисперсионный анализ

Условие: имеются выборочные данные по результатам однофакторного многовариантного эксперимента, число наблюдений по вариантам опыта (выборкам) одинаково

Требуется: установить наличие или отсутствие различий между вариантами в генеральных совокупностях.

1.1) выдвигаем две гипотезы, в качестве нулевой - все m генеральных средних равны между собой, то есть : 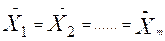; в качестве альтернативной выдвигается предположение, что хотя бы две генеральных средних не равны между собой;: ;

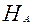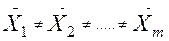1.2) определяемся с уровнем значимости;

1.3) в качестве критерия при воспользуемся критерием F-Фишера.

1.4) фактическое значение критерия определим по формуле (при условии, что . Если в ходе расчетов дисперсий оказалось, что критерий F-Фишера не рассчитывается, а сразу признается справедливой нулевая гипотеза о равенстве генеральных средних.. Для получения необходимых дисперсий вначале следует разложить общий объем вариации на составные части в соответствии с известным законом: . Поскольку речь идет о выборочных дисперсиях 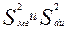для их получения необходимо соответствующие объемы вариации разделить на их степени свободы – для межгрупповой вариации: df (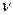) = m-1, где m – число средних;для внутригрупповой вариации df (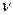)= (N-1)-(m-1), где N – общее число наблюдений по всем выборкам, то есть , а а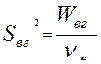

1.5) найдем табличное значение критерия, которое зависит от уровня значимости и от степеней свободы df (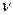) = m-1 и df (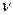)= (N-1)-(m-1), Сравнение фактического значения критерия с табличным позволяет сформулировать соответствующие выводы.

1.6) если по F – критерию была принята альтернативная гипотеза, то следует провести конкретизацию дисперсионного анализа с использованием критерия Q- Тьюки

Использование критерия Q - Тьюки в целях конкретизации включает следующие шаги:

1.6.1) рассчитываем средние значения признака по группам (выборкам)

, …..;

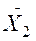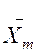1.6.2) полученные средние ранжируем, например ранжированный ряд может выглядеть так: ,…..;

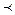
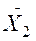
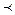
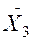
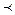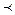
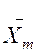1.6.3) находим разности первого порядка, под которыми понимаются

разности между средними соседними в ранжированном ряду, например, 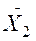-; 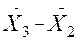и так далее;

1.6.4) находим разности второго порядка, то есть разности между средними стоящими в ранжированном ряду через одну позицию, то есть

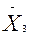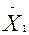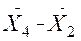-, и так далее.

1.6.5) находим разности следующих порядков, если для этого имеются необходимые средние;

1.6.6) относительно каждой из разностей выдвигаются две гипотезы: нулевая (Н0) –в генеральной совокупности разность равна 0 (нулю) иными словами в генеральной совокупности соответствующие средние равны между собой и альтернативная (НА) - в генеральной совокупности разность нулю не равна, то есть соответствующие генеральные средние не равны между собой;

1.6.7) для каждой разности находим ее среднюю ошибку по формуле:

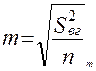, где 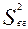- внутригрупповая дисперсия, 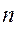- число наблюдений в каждой группе (выборке).

1.6.8) каждую из разностей первого порядка разделим на среднюю ошибку, получим фактические значения критерия Q-Тьюки для разностей первого порядка, то есть 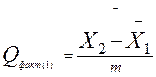, 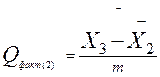и так далее.

1.6.9) полученные фактические значения критерия Q-Тьюки сравниваем с табличным, которое для всех разностей первого порядка одинаково. Табличное значение критерия Q-Тьюки зависит от уровня значимости, числа степеней свободы внутригрупповой вариации и от величины k, которая для разностей первого порядка равна 2. Сравнение позволяет принять относительно пары средних или нулевую гипотезу (средние равны между собой) или альтернативную гипотезу (средние составляющие пару не равны между собой);

1.6.10) каждую из разностей второго порядка разделим на среднюю ошибку и получим фактические значения критерия Q-Тьюки для разностей второго порядка. Все фактические значения критерия Q-Тьюки сравниваются с одним и тем же табличным, которое зависит от принятого уровня значимости, числа степеней свободы внутригрупповой вариации и величины k, которая для разностей второго порядка равна 3. Сравнение даст основание для принятия нулевой (равенство средних) или альтернативной (неравенство средних) гипотезы.

Аналогичная процедура осуществляется относительно разностей третьего, четвертого и так далее порядков.

Дата добавления: 2014-01-07