Основные понятия теории игр

ОСНОВЫ ТЕОРИИ ИГР

Аппарат теории игр предназначен для выбора оптимального решения в условиях неопределенности, т. е. в ситуациях, когда отсутствует полная информация, необходимая для выбора решения.

Первые работы по теории игр относятся к началу ХХ в. Основателем теории игр является американский ученый–математик Дж. фон Нейман, который в 1928 г. доказал основополагающую теорему теории игр – теорему о минимаксе.

Определенную роль в развитии теории игр сыграло создание и совершенствование ЭВМ.

Главным в исследовании игр является понятие оптимальных стратегий игроков. В это понятие интуитивно вкладывается такой смысл: стратегия игрока является оптимальной, если применение этой стратегии обеспечивает ему наибольший гарантированный выигрыш при всевозможных стратегиях другого игрока. Исходя из этих позиций, игрок 1 исследует матрицу выигрышей А следующим образом: для каждого значения i (i =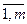) определяется минимальное значение выигрыша в зависимости от применяемых стратегий игрока 2: а_ij (i = 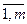), т.е. определяется минимальный выигрыш для игрока 1 при условии, что он примет свою i -ю чистую стратегию, затем из этих минимальных выигрышей отыскивается такая стратегия i = i_о, при которой этот минимальный выигрыш будет максимальным, т.е. находится по формуле:

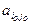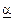а_ij == (7).

Число 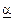, определённое по формуле (7) называется нижней чистой ценой игры и показывает, какой минимальный выигрыш может гарантировать себе игрок 1, применяя свои чистые стратегии при всевозможных действиях игрока 2. Игрок 2 при оптимальном своём поведении должен стремится по возможности за счёт своих стратегий максимально уменьшить выигрыш игрока 1. Поэтому для игрока 2 отыскивается 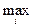а_ij, т.е. определяется max выигрыш игрока 1, при условии, что игрок 2 применит свою j -ю чистую стратегию, затем игрок 2 отыскивает такую свою j = j₁ стратегию, при которой игрок 1 получит min выигрыш, т.е. находится по формуле:

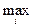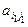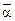a_ij == (8).

Число 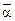, определяемое по формуле (8), называется чистой верхней ценой игры и показывает, какой максимальный выигрыш за счёт своих стратегий может себе гарантировать игрок 1. Другими словами, применяя свои чистые стратегии игрок 1 может обеспечить себе выигрыш не меньше 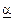, а игрок 2 за счёт применения своих чистых стратегий может не допустить выигрыш игрока 1 больше, чем .

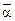Если в игре с матрицей А 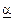=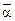, то говорят, что эта игра имеет седловую точку в чистых стратегиях и чистую цену игры n = =.

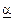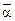Седловая точка – это пара чистых стратегий (i_о,j_о) соответственно игроков 1 и 2, при которых достигается равенство 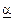= 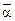. В это понятие вложен следующий смысл: если один из игроков придерживается стратегии, соответствующей седловой точке, то другой игрок не сможет поступить лучше, чем придерживаться стратегии, соответствующей седловой точке.

Задача № 4.1.

Задана платежная матрица игры A, необходимо найти решение игры:

A =элементы a_ij.

Найдем стратегию действия для первого игрока, согласно условию 7–это maxmin стратегию, т.е. необходимо проанализировать столбцы матрицы A, выбрать в них минимальные элементы, а затем из этих минимальных элементов выбрать максимальный, и тем самым будет определена стратегия для 1-го игрока.

1-й игрок.

Для первого столбца, min ₁=3, для второго столбца– min ₂=1 и для третьего– min ₃=2. Теперь анализируем минимальные элемента на max:{3, 1, 2}=3. Таким образом, для первого игрока целесообразно действовать 1-й стратегией.

2-й игрок.

Для второго игрока по такой же схеме отыскивается наилучшее решение, только здесь необходимо считать minmax стратегию.

Для первой строки, max ₁=7, для второй строки max ₂=6 и третье– max ₃=8. Анализируем максимальные элементы на min:{7, 6, 8}=6. Для второго игрока целесообразно действовать 2-й стратегией.

Подведем анализ решения:

Таким образом, решение не является седловой точкой, так как верхнее значение игры не совпадает с нижним значением игры.

Задача № 4.2.

Построить ЭММ и используя программный комплекс «Блок-3» определить оптимальные стратегии в сражениях для армий А и В.

A: (3,0,7)(2,6,2)(6,1,3)(4,0,6)(1,5,4),

B: (7,0,3)(2,3,5)(6,3,1)(5,0,5)(3,6,1).

Определим план процесса решения задачи на основании теории игр.

Для определения оптимальной стратегии в сражении, необходимо определить «правило игры», т.е. сражения:

– за каждое уничтоженное подразделение дается одно очко;

– за каждую взятую высоту – одно очко;

– в случае равенства подразделений в сражении за высоту, дается 0 очков.

Таблица 27

Платежная матрица игры

А + В –	(3,0,7)	(2,6,2)	(6,1,3)	(4,0,6)	(1,5,4)	max	min max
(7,0,3)	–4+0+4	–3+1–3	–7+1+0	–5+0+4	–2+1+4
	–5	–6	–1
(2,3,5)	+3–1+6	0+4–3	+3–2–4	+3–1+6	–2+4–5
		–3		–3
(6,3,1)	–4–1+2	–3+4+2	0–2+2	–5–1+2	–2+4+2
–3			–4
(5,0,5)	–4+0+6	–3+1–3	+6+1–4	–5+0+6	–2+1–5
	–5			–6
(3,6,1)	0–1+2	–3+0+2	+4–2+2	+4–1+2	–2–6+2
	–1			–6
min	–3	–5	–6	–4	–6	3 –3
max min	–3

Выигрыш является седловой точкой, так как 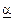= 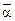(A (3,0,7), B (7,0,3)).

В скобках указана стратегия (три числа – три высоты, значение –количество подразделений направленных для взятия этой высоты). Целесообразно весь ход сражения записать в платежную матрицу игры (табл. 27) для полного анализа сражения.

Победы в сражениях армии А обозначаем со знаком + (плюс), армии В со знаком – (минус). В числителе результаты сражений за высоты (результаты суммируются), знаменателе – общий итог сражений за высоты, знак + означает победу армии А, знак – победу армии В.

Предположим, что цена игры положительна (n > 0). Если это не так, то всегда можно подобрать такое число с, прибавление которого ко всем элементам матрицы выигрышей даёт матрицу с положительными элементами, и следовательно, с положительным значением цены игры. При этом оптимальные смешанные стратегии обоих игроков не изменяются.

Итак, пусть дана матричная игра с матрицей А порядка . Согласно оптимальным смешанным стратегиям х = (х_i,..., х_m), y = (yj,..., y_n) соответственно игроков 1 и 2 и цена игры n должны удовлетворять соотношениям.

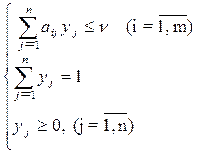
(9) (10).

Разделим все уравнения и неравенства в (9) и (10) на n (это можно сделать, т.к. по предположению n > 0) и введём обозначения:

, ,

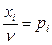
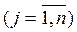Тогда (9) и (10) перепишется в виде:

, , , ,

, , , .

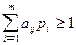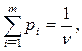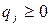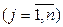Поскольку первый игрок стремится найти такие значения х_i и, следовательно, p_i, чтобы цена игры n была максимальной, то решение первой задачи сводится к нахождению таких неотрицательных значений p_i 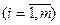, при которых

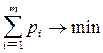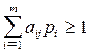, (11).

Поскольку второй игрок стремится найти такие значения y_j и, следовательно, q_j, чтобы цена игры n была наименьшей, то решение второй задачи сводится к нахождению таких неотрицательных значений q_j, , при которых

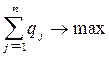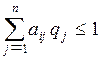, . (12).

Формулы (11) и (12) выражают двойственные друг другу задачи линейного программирования (ЛП).

Решив эти задачи, получим значения p_i 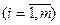, q_j и n. Тогда смешанные стратегии, т.е. x_i и y_j получаются по формулам:

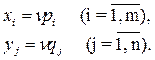(13).

Для преобразования данной задачи к ЭММ ЛП, необходимо взять значение числа с равным 6 (прибавить число 6 к результатам сражений, т. е. выигрышам) и согласно (11) и (12), исходная задача будет представлена:

Армия А Армия В

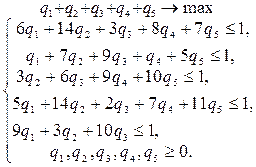Введя данные в программный комплекс «Блок-3», получим следующие решения: цена игры равна n=5,6497.

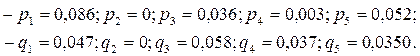
Учитывая (13) получим следующие стратегии:

Задача № 4.3.

Игры с природой. Планирование посевов.

Фермер планирует посеять три вида культур: А ₁, А ₂ и А ₃. Урожай этих культур зависит главным образом от погоды, которая может находиться в трех состояниях: В ₁, В ₂ и В ₃. Информация зависимости урожайности от погоды отображена в табл. 28.

Таблица 28

Дата добавления: 2014-01-07