Оценка согласованности экспертов

При ранжировании объектов эксперты обычно расходятся во мнениях по решаемой проблеме. В связи с этим, возникает необходимость количественной оценки степени согласия экспертов. Получение количественной меры согласованности мнений экспертов позволяет более обоснованно интерпретировать причины в расхождении мнений и определить возможность отнесения решаемой проблемы к проблемам первого класса, т.е. проблемам с достаточным информационным потенциалом.

В настоящее время известны две меры согласованности мнений группы экспертов: дисперсионный и энтропийный коэффициенты конкордации (коэффициенты согласия).

Дисперсионный коэффициент конкордации. Рассмотрим матрицу результатов ранжировки m объектов группой из d экспертов || r_is || (s = 1,..., d; i = 1,..., m), где r_is – ранг, присваиваемый s -м экспертом i -му объекту. Составим суммы рангов по каждой строке. В результате получим вектор с компонентами

(13)

Будем рассматривать величины г₁ как реализации случайной величины и найдем оценку дисперсии. Как известно, оптимальная по критерию минимума среднего квадрата ошибки оценка дисперсии определяется формулой (14):

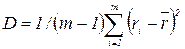, (14)

где 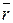– оценка математического ожидания, равна

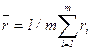. (15)

Дисперсионный коэффициент конкордации определяется как отношение оценки дисперсии (14) к максимальному значению этой оценки

W = D / D_max (16)

Коэффициент конкордации изменяется от нуля до единицы, поскольку 0 £ D £ D_max.

Максимальное значение дисперсии равно

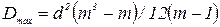(17)

Введем обозначение

(18)

Используя (18) запишем дисперсии (14) в виде

D = 1 / (m – 1) ´ S (19)

Подставляется (17) и (19) в (16) и сокращая на множитель (m - 1), запишем окончательное выражение для коэффициента конкордации

W = 12 / d² (m³ - m) ´ S (20)

Данная формула определяет коэффициент конкордации для случая отсутсвия связанных рангов.

Если в ранжировках имеются связанные ранги, то максимальное значение дисперсии в знаменателе формулы (16) становится меньше, чем при отсутствии связанных рангов. Можно показать, что при наличии связанных рангов коэффициент конкордации вычисляется по формуле

(21)

где

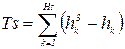(22)

В формуле (22) Ts - показатель связанных рангов в s -й ранжировке, Hs - число групп равных рангов в s - й ранжировке, h_k - число равны рангов в k - й группе связанных рангов при ранжировке s_м экспертом. Если совпадающих рангов нет, то Hs = 0, hk = 0, следовательно, Ts = 0. В этом случае формула (21) совпадает с формулой (20).

Коэффициент конкордации равен 1. если все ранжировки экспертов одинаковы. Коэффициент конкордации равен нулю, если все ранжировки различны, т.е. совершенно нет совпадения. Коэффициент конкордации, вычисляемый по формулам (20) и (21) является оценкой истинного значения коэффициента и, следовательно, представляет собой случайную величину. Для определения значимости оценки коэффициента конкордации необходимо знать распределение частот для различных значений числа экспертов d и количества объектов m. Распределение частот для W при 3 £ d £ 20 и 3 £ m £7 дано в работе (25). Для большинства значений m и d можно использовать известные статистике данные. При числе объектов m > 7 оценка значимости коэффициента конкордации может быть произведена по критерию c². Величина d(m - 1) W имеет W_c2 распределение с u = (m - 1) степенями свободы.

При наличии связанных рангов c² распределение с u = (m - 1) степенями свободы имеет величина

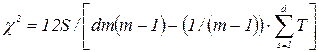(23)

Пример 1. Результаты ранжировнаия шести объектов (m = 6) пятью экспертами (d = 5) представлены в табл. 10. Вычислим коэффициент конкордации и произведем оценку его значимости. Среднее значение r равно

.

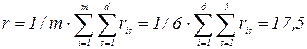Величина, S в соответствии с формулой (14) равна

.

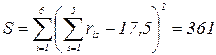Поскольку в ранжировках имеются связанные ранги, то вычисление коэффициента выполним по формуле (21). Предварительно вычислим величины Т_s, используя формулу (22).

Т₁ = 2³ - 2 = 6; Т₄ = 2³ - 2 + 2³ - 2 = 12;

Т₂ = 3³ - 3=24; Т₅ = 2³ - 2 = 6.

Т₃ = 2³ - 2 + 2³ - 2 = 12;

Таблица 10

Эs Oi	Э1	Э2	Э3	Э4	Э5
O1			1,5
O2	2,5		1,5	2,5
O3	2,5			2,5
O4			4,5	4,5
O5			4,5	4,5	5,5
O6					5,5

Представляя значения Т_s, S и m = 6, d = 5 в формулу (21) и производя вычисления, получаем

W = 12 × 361 / (5² - 6) - 5 × 60) = 0.874.

Оценим значимость коэффициентов конкордации. В данном случае число степеней свободы n = 5. Табличное значение c² для n = 5 и 5% уровня значимости c² табл. = 11,07. Подставляя значения величины в формулу (23), получаем

.

Поскольку 11,07 < 21,8, то гипотеза о согласии экспертов в ранжировках принимается.

Энтропийный коэффициент конкордации определяется формулой (24):

W_Э = 1 - H / H_max, (24)

где Н – энтропия, вычисляемая по формуле

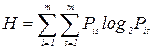, (25)

а Н_max – максимальное значение энтропии. В формуле для энтропии Р_is – оценки вероятностей s -го ранга, присваиваемого; i -му объекту. Эти оценки вероятностей вычисляются в виде отношения количества экспертов, приписавших объекту О_i ранг s к общему числу экспертов d

P_is = d_is / d (26)

Максимальное значение энтропии достигается при равновероятном распределении рангов, т.е. когда d_is = d / m. Тогда

P_is = d / dm = 1 / m (27)

Подставляя это соотношение в формулу (25), получаем

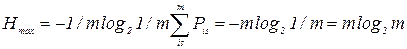(28)

Коэффициент согласия изменяется от нуля до единицы. При W_э = 0 расположение объектов по рангам равновероятно, поскольку в этом случае Н ~ Н_max, Данный случай может быть обусловлен либо невозможностью ранжировки объектов по сформулированной совокупности показателей, либо полной несогласованностью мнений экспертов. При W_э = 1, что достигается при нулевой энтропии (Н = 0), все эксперты дают одинаковую ранжировку. Действительно, в этом случае для каждого фиксированного объекта О_i все эксперты присваивают ему один и тот же ранг, следовательно Р_is = 1, и Р_ks = 0 (k ¹ s, k = 1,..., m). Поэтому и Н = 0.

Сравнительная оценка дисперсионного и энтропийного коэффициентов конкордации показывает, что эти коэффициенты дают примерно одинаковую оценку согласованности экспертов при близких ранжировках. Однако, если, например, вся группа экспертов разделилась во мнениях на две подгруппы, причем ранжировки в этих подгруппах противоположные (прямая и обратная), то дисперсионный коэффициент конкордации будет равен нулю, а энтропийный коэффициент конкордации будет равен 0,7. Таким образом, энтропийный коэффициент конкордации позволяет зафиксировать факт разделения мнений на две противоположные группы. Объем вычислений для энтропийного коэффициента конкордации несколько больше, чем для дисперсионного коэффициента конкордации.

Дата добавления: 2014-01-07