Корректность МНК

Доказано, что решение системы (3.12) существует и единственно, если столбцы матрицы Ф линейно независимы (строки могут быть любыми, даже могут повторяться – т.е. эксперименты могут проводиться при одинаковых значениях x_i). Если столбцы линейно зависимы, то det (Ф^T Ф) = 0 и решения нет.

Если столбцы «почти» линейно зависимы, то система (3.12) плохо обусловлена со всеми вытекающими последствиями.

Пример 3.6. Пусть x_i) = 101, 102, …, 106; f ₁(x) = x; f ₂(x) º 1. Тогда

Ф^T Ф = .

Поделим первый столбец на 103.5, получим матрицу

,

т.е. матрица почти вырождена. Это произошло потому, что x_i относительно близки между собой. Чтобы этого не произошло, часто бывает полезно «отцентрировать» x_i, т.е. сделать замену переменных 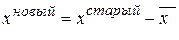, где

.

В данном случае = 103.5. Новые данные: x_i = –2.5, –1.5, …, 2.5. Тогда

Ф^T Ф = ,

Система стала хорошо обусловленной.

Кроме того, при вычислении элементов матрицы Ф и при остальных действиях все операции надо выполнять с высокой точностью, т.к. плохо обусловленные системы очень чувствительны к погрешностям округления.

Приложение 1.

const nn=15; { МЕТОД ГАУССА. ПРОСТОЙ ВАРИАНТ }

type masA=array[1..nn,1..nn] of real;

masX=array[1..nn] of real;

var mtr:masA; x:masx;

i,j,n:integer;

s:real;

error:boolean;

procedure Gauss(var aa:masA; var b:masX;

n:integer; var error:boolean);

var i,j,k,m: integer;

a0,a1: real;

begin error:=false;

{ ПРЯМОЙ ХОД }

for k:=1 to n-1 do

begin { ПОИСК ВЕДУЩЕЙ СТРОКИ}

error:=true;

for i:=k to n do

if aa[i,k] <> 0 then {***}

begin error:=false; m:=i; break

end;

if error then exit;

if m<>k then

begin for j:=1 to n do { ОБМЕН }

begin s:=aa[m,j];

aa[m,j]:=aa[k,j]; aa[k,j]:=s;

end;

s:=b[m]; b[m]:=b[k]; b[k]:=s;

end;

{ ПРЕОБРАЗОВАНИЕ СТРОК }

a0:=aa[k,k];

for j:=k to n do aa[k,j]:=aa[k,j]/a0;

b[k]:=b[k]/a0;

for i:=k+1 to n do

if aa[i,k] <> 0 then

begin a1:=aa[i,k];

for j:=k to n do

aa[i,j]:=aa[i,j]/a1 - aa[k,j];

b[i]:=b[i]/a1 - b[k];

end;

end;

{ ОБРАТНЫЙ ХОД }

if aa[n,n]=0 then

begin error:=true; exit; end;

b[n]:=b[n]/aa[n,n];

for i:=n-1 downto 1 do

begin s:=b[i];

for j:=i+1 to n do s:=s-aa[i,j]*b[j];

b[i]:=s;

end;

end;

{ ГОЛОВНАЯ ПРОГРАММА }

begin readln(n);

for i:=1 to n do

begin for j:=1 to n do read(mtr[i,j]);

readln(x[i]);

end;

Gauss(mtr,x,n, error);

writeln;

if error then writeln(' СИСТЕМА ВЫРОЖДЕНА ')

Дата добавления: 2014-01-07