Связь векторного и координатного способов

Пусть движениеточки задается координатным способом.

В таком случае формулы (1.1.13) и (1.1.15):

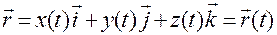, (1.1.13)

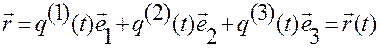, (1.1.15)

определяют вектор-функцию 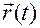, которая является основой для векторного способа задания движения.

Пусть теперь движениеточки задается векторным способом.

Тогда из (1.1.13) и (1.1.15) можем получить координатный способ задания движения, если вычислим координаты вектор-функции .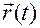

Будем смотреть на равенства (1.1.13) и(1.1.15) как на уравнения относительно указанных координат. В этих уравнениях известными являются вектор-функции 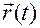и базисные векторы.

Если системой отсчета является система 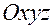, то, умножая (1.1.13) скалярно на 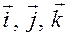последовательно, получим

, , .

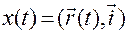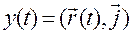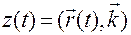Здесь

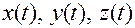— координаты точки, вычисленные по ее заданному положению 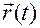в любой момент времени .

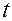Как видно из этих выражений, геометрические координаты точки в любой момент времени 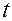равны ортогональным проекциям вектор-функции 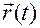на оси системы отсчета 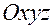в момент времени .

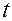Аналогично, если система отсчета является аффинной 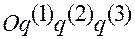, то, умножая (1.1.15) последовательно скалярно на векторы

, , ,

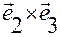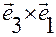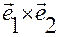получим

.

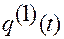
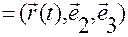Отсюда

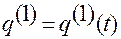
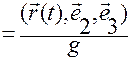, (1.1.19)

где введено обозначение .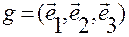

Примечание 2

Легко показать, что

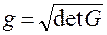, если система координат правая;

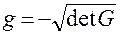, если эта система левая.

Аналогично при умножении (1.1.15) скалярно на (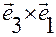) и на (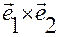), получим

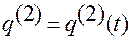
, (1.1.20)

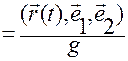. (1.1.21)

Такими действиями находятся координаты 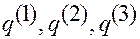точки 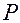в аффинной системе при известном векторе .

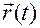Примечание 3

Выражения (1.1.20) и (1.1.21):

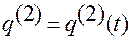
, (1.1.20)

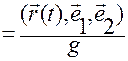(1.1.21)

легко можно записать, зная формулу (1.1.19):

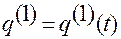
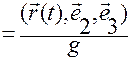, (1.1.19)

Обозначим последовательность индексов у переменных 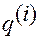, в виде

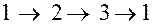(1.1.22)

и последовательность индексов у ортов также в виде

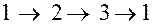. (1.1.23)

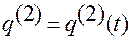
Тогда соотношение (1.1.20)

, (1.1.20)

получается из (1.1.19)

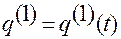
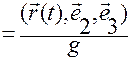, (1.1.19)

заменой в равенстве (1.1.19) индекса «1» при на следующий за ним индекс «2» в последовательности (1.1.22)

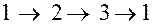, (1.1.22)

и заменой индексов «2» и «3» у ортов на следующие за ними в последовательности (1.1.23)

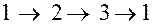(1.1.23)

индексы «3» и «1», соответственно.

После записи выражения (1.1.20) соотношение (1.1.21)

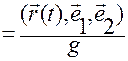. (1.1.21)

строится аналогичным образом из (1.1.20) по правилу замены индексов при и согласно схемам (1.1.22) и (1.1.23).

Если две или более формулы выводятся последовательно друг из друга заменой переменных и (или) индексов на их другие значения из заданных упорядоченных последовательностей, то говорят, что:

Дата добавления: 2014-01-07