Дискретный спектр стационарной случайной функции

А) Частоты - произвольные числа, количество их конечно.

Пусть стационарная случайная функция X(t) может быть представлена в виде спектрального разложения

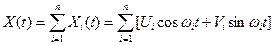(4)

причем, сохраняются допущения .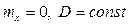

Найдем дисперсию одной гармоники X_i(t), учитывая, что следующие величины U_i и V_i не коррелированы и дисперсии величин с одинаковыми индексами равны между собой: :

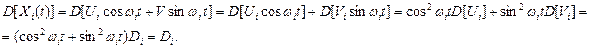
Итак,

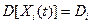. (5)

Таким образом, дисперсия i -й гармоники спектрального разложения (4) равна дисперсии случайной величины U_i, или, что то же, дисперсии случайной величины V_i.

Найдем теперь дисперсию стационарной случайной функции X(t), принимая во внимание, что слагаемые Х_i(t) не коррелированы и поэтому дисперсия их суммы равна сумме дисперсий слагаемых:

.

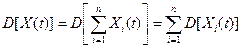Используя (5), получим .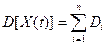

Итак, дисперсия стационарной случайной функции, которая может быть представлена в виде суммы конечного числа гармоник с произвольными частотами, равна сумме дисперсий составляющих ее гармоник.

Определение 2.2. Дискретным спектром стационарной случайной функции X(t) вида (4) называется совокупность дисперсий всех составляющих ее гармоник.

Заметим, так как каждой частоте можно поставить в соответствие дисперсию 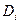, то спектр можно изобразить графически: на горизонтальной оси откладываем , а в качестве ординаты (спектральных линий) строят дисперсии 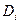. Этот дисперсионный спектр называют линейчатым.

Б) Равностоящие частоты, множество их бесконечное (счетное).

Рассмотрим спектральное разложение вида

,

в котором число частот бесконечно (счетно), они равноотстоящие, причем разность любых двух «соседних» частот

,

где Т - действительное положительное число.

Таким образом,

; ; …, , …

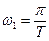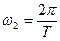Корреляционная функция рассматриваемой стационарной случайной функции X(t), при , n = ¥, имеет вид:

. (6)

При t = 0, учитывая, что k_х(0) = D_x, получим

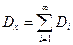(7)

Итак, дисперсия стационарной случайной функции, которая может быть представлена в виде суммы бесконечного (счетного) множества гармоник с равноотстоящими частотами, равна сумме дисперсий слагаемых гармоник.

Соотношение (6) можно рассматривать как разложение корреляционной функции в ряд Фурье по косинусам. Из (6) видно, что k_х(t) - периодическая функция с периодом 2Т, поэтому коэффициенты Фурье

,

или, учитывая, что 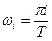и подынтегральная функция - четная,

.

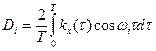Если каждой частоте 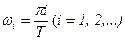ставить в соответствие дисперсию 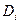, то получим, как и в случае конечного числа произвольных частот, дискретный линейчатый спектр, причем число спектральных линий (ординат 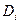) бесконечно (счетно) и они равноотстоящие.

Теорема 2.1. Если ковариационная функция К_x(t) скалярного стационарного случайного процесса , с нулевым математическим ожиданием является непрерывной на отрезке [ -l, l ], удовлетворяет на нем условиям Дирихле и представима в виде

,

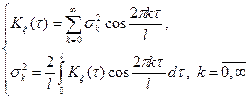то случайный процесс 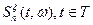, определяемый

,

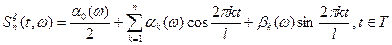является стационарным (где 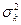-.дисперсия случайных амплитуд a_k(w) и b_k(w), соответствующих частоте ).

Дата добавления: 2014-01-07