Свойства НОД

Евклида. Соотношение Безу. Наименьшее общее кратное

Наибольший общий делитель целых чисел. Алгоритм

Определение 1.2.1. Если целые числа а ₁, а ₂,…, а_n, n ³ 2, делятся на целое d ¹ 0, то d называют их общим делителем (ОД).

В дальнейшем речь пойдет только о положительных целых делителях.

Определение 1.2.2. Максимальный из общих делителей целых чисел а ₁, а ₂,…, а_n, хотя бы одно из которых отлично от нуля, называется их наибольшим общим делителем (НОД) и обозначается НОД(а ₁, а ₂,…, а_n) или (если это не вызывает разночтений) (а ₁, а ₂,…, а_n).

1. d Î N.

2. d | a_i, .

3. Для " d: d | a_i, , Þ d | d.

Определение 1.2.2 НОД целых чисел а ₁, а ₂,…, а_n равносильно выполнению свойств 1–3.

4. НОД целых чисел единственный.

Пусть d и d ₁ – два НОД целых чисел а ₁, а ₂,…, а_n, n ³ 2. Тогда по свойству 3 НОД d ₁ | d & d | d ₁ Û | d | = | d ₁ | по свойству 4 делимости целых чисел. Так как d, d ₁ Î N, то d = d ₁.

Очевидно, что если b | a, то (a, b) = | b |.

Теорема 1.2.1. Если 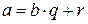, то (a, b) = (b, r).

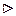По свойству 6 делимости целых чисел – ОД b и r, 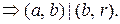По свойствам 5, 6 делимости целых чисел (b, r) – ОД a и b, Согласно свойству 4 делимости целых чисел, поскольку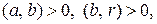

Это наблюдение (теорема 1.2.1) позволило выдающемуся древнегреческому математику Евклиду (III в. до н.э.) обосновать следующий факт, являющийся по сути кратным применением теоремы 1.2.1.

Теорема 1.2.2 (Евклид). Наибольший общий делитель целых чисел a и b при условии, что | a | > | b |, , равен последнему отличному от нуля остатку от деления в цепочке равенств:

a = b × q ₁ + r ₁,

b = r ₁ × q ₂ + r ₂, если ,

…

r_{n – 2} = r_{n – 1} × q_n + r_n, если ,

r_{n – 1} = r_n × q_{n + 1}, если .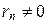

То есть .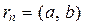

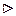Согласно теореме 1.2.1 и поскольку 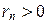, как остаток от деления, имеем

(a, b) = (b, r ₁) = (r ₁, r ₂) = … = (r_{n – 1}, r_n) = r_n.

Процесс получения (a, b) конечен, поскольку мы оперируем только с целыми числами и, начиная с деления r ₁ на r ₂, – с целыми положительными числами. Идет постоянное уменьшение остатков r_i: 0 £ r_i < r_{i – 1}, и за конечное число шагов будет достигнут остаток r_{n + 1} = 0.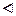

Пример 1.2.1. Найти (72, 26).

Решение. ;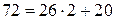

;

;

.

Следовательно, (72, 26) = 2. ·

Теорема 1.2.2 дает алгоритм Евклида нахождения НОД целых чисел. Он с помощью рекурсии легко преобразуется в алгоритм нахождения НОД не только двух, но и большего количества целых чисел: (a ₁,…, a_{n – 1}, a_n) = ((a ₁,…, a_{n – 1}), a_n), n = 3, 4,… Алгоритм Евклида остается в классе самых быстрых алгоритмов нахождения НОД целых чисел.

Обратное применение цепочки равенств теоремы 1.2.2, равно как и выражение на каждом шаге остатка от деления в виде целочисленной линейной комбинации a и b – так называемый расширенный алгоритм Евклида – доказывает следующий факт.

Теорема 1.2.3. Если d = (a, b), то существуют такие целые u и v, что выполняется соотношение:

d = u × a + v × b.

Если a | b, то d = | a |,

Если b | a, то d = | b |,

Если , , то, не ограничивая общности, можем считать | a | > | b | и согласно теореме 1.2.2 получаем:

,

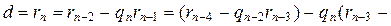
где u, v Î Z. Используя расширенный алгоритм Евклида, получим те же значения u и v:

r ₁ = a – q ₁ b,

r ₂ = b – q ₂ r ₁ = b – q ₂(a – q ₁ b) = – q ₂ a + (1 + q ₂ q ₁) b,

…

d = r_n = r_{n – 2} – q_nr_{n – 1} = … = ua + vb.

Следствие. Пусть d = (а ₁, а ₂,…, а_n). Тогда существуют такие u ₁, u ₂,…, u_n Î Z, что

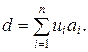(1.2.1)

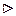Для n = 2 равенство (1.2.1) справедливо согласно теореме 1.2.3. При n ³ 2 сделаем индуктивное предположение о справедливости равенства (1.2.1). Поскольку , то согласно теореме 1.2.3 получаем соотношение: 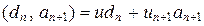. Тогда 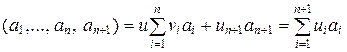. Таким образом, равенство (1.2.1) справедливо для любого натурального n ³ 2.

Определение 1.2.3. Равенство (1.2.1) называют соотношением Безу для наибольшего общего делителя целых чисел.

Пример 1.2.2. Из примера 1.2.1 следует, что

2 = 20 + 6 × (–3) = 20 + (26 + 20 × (–1)) × (–3) = 20 × 4 + 26 × (–3) =

= (72 + 26 × (–2)) × 4 + 26 × (–3) = 72 × 4 + 26 × (–11).

2 = 72 × u + 26 × v, u = 4, v = –11. ·

Замечание. Числа 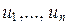в (1.2.1) не являются единственными с таким условием. Это следует из теории диофантовых линейных уравнений, которая будет рассмотрена ниже. Так, в примере 1.2.2 числа u = – 9 и v = 25 также удовлетворяют соотношению Безу.

Определение 1.2.4. Если целые, отличные от нуля числа а ₁, а ₂,…, а_n, n ³ 2, делят целое m, то m называют их общим кратным (ОК).

В дальнейшем речь здесь пойдет только о положительных целых кратных.

Определение 1.2.5. Минимальное из общих кратных целых чисел а ₁, а ₂,…, а_n называется их наименьшим общим кратным (НОК) и обозначается НОК(а ₁, а ₂,…, а_n) или (если это не вызывает разночтений) [ а ₁, а ₂,…, а_n ].

Дата добавления: 2014-01-07