Позиционные системы счисления и методы перевода чисел

Представление информации в цифровых автоматах

В привычной для нас десятичной системе счисления используют 10 цифр: 0,1,2,…,9 и каждое число представлено как:

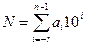
где i – номер разряда,

a – одна из цифр от 0 до 9,

r – количество разрядов в дробной части числа,

n - количество разрядов в целой части числа.

Например, 405.35=4*10²+0*10¹+5*10⁰+3*10^-1+5*10^-2

Но десятичная система счисления далеко не единственно возможная. В общем случае число N в некоторой позиционной системе счисления с основанием P записывается как

,

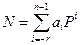где a –цифра от 0 до P-1,

P – основание системы счисления.

Позиционными системами счисление называются такие, у которых вес каждой цифры a зависит от позиции в изображении числа. Так римская система счисления непозиционная.

Максимальное целое число, которое может быть представлено в n разрядах:

.

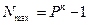Минимальное значащее (не равное 0) число, которое можно записать в r разрядах дробной части:

.

Для представления информации в ЭВМ используется двоичная или двоично-десятичная система счисления. В двоичной системе только две цифры 0 и 1. Важное достоинство двоичной системы счисления – удобство физического представления цифр.

Любое число в двоичной системе представляет несколькими двоичными разрядами, каждый разряд несет информацию равную 1 биту. Поэтому каждый разряд и называют просто битом. Пример двоичного числа с дробной частью:

1010.001₂=1*2³+0*2²+1*2¹+0*2⁰+0*2^-1+0*2^-2+1*2^-3=10.125₁₀.

Недостаток двоичной системы – слишком громоздкая запись. Например,

173₁₀=10101101.

Поэтому она используется «внутри» ЭВМ, а для представления двоичных кодов человеку часто применяют восьмеричную и шестнадцатеричную системы счисления. В восьмеричной используют цифры от 0 до 7. Например,

257₈=2*8²+5*8¹+7*8⁰=175₁₀.

В шестнадцатеричной используют цифры от 0 до 9 и добавляются новые цифры: A = 10, B = 11, C = 12, D = 13, E = 14, F = 15.

Например, 3E5A1₁₆=3*16⁴+E*16³+5*16²+A*16¹+1*16⁰=3*16⁴+14*16³+5*16²+10*16¹+1*16⁰ =255393₁₀

Чем больше основание СС, тем компактнее запись чисел.

Итак, выше приведены примеры перевода чисел из двоичной, восьмеричной и шестнадцатеричной систем счисления в десятичную.

Алгоритм обратного перевода заключается в следующем. Число в десятичной системе счисления последовательно делится на основание системы счисления, в которую надо переводить. В качестве цифр нового представления берутся остатки от деления в обратном порядке, начиная с младшего остатка.

На рис.3 приведен пример перевода 10₁₀ в двоичную систему.

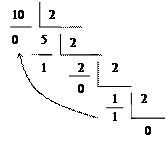Рис.3

Таким образом, 10₁₀=1010₂.

Для перевода дробных частей десятичных чисел используют следующий алгоритм. Число в десятичной системе счисления необходимо последовательно умножать на основание системы счисления, в которую надо переводить. Причем умножать надо только очередную дробную часть, игнорируя возникающие целые части. В качестве цифр берутся целые части результатов умножения. Так происходит до тех пор, пока дробная часть не станет равной нулю или не достигается заданная точность.

На рис.4 приведен пример перевода 0.625₁₀ в двоичную систему счисления.

Рис.4

Таким образом, 0.625₁₀=0.101₂.

Для перевода из двоичной в восьмеричную систему счисления число в двоичной системе необходимо разбить по три цифры (на триады) справа налево, и вместо каждой триады записать восьмеричную цифру соответствующую двоичному коду триады. Например, необходимо перевести 1101111011₂ в восьмеричную систему счисления, тогда

001 101 111 011

1 5 7 3

Таким образом, 1101111011₂=1573₈.

Аналогично, при переводе в шестнадцатеричную систему счисления двоичное число разбивается по четыре цифры (на тетрады). Например, переведем 1101111011₂ в шестнадцатеричную систему счисления.

0011 0111 1011

3 7 11

Таким образом, 1101111011₂=37В₁₆.

Обратный перевод из восьмеричной или шестнадцатеричной системы счисления в двоичную очень прост, каждая цифра записывается в двоичном коде по триадам или тетрадам.

123₈ = 1 010 011₂

А17₁₆ = 1010 0001 0111₂.

Для изображения двоичных чисел часто используют двоично-десятичную систему счисления. В этой системе для изображения каждой десятичной цифры отводится тетрада. Например, десятичное число 925 в двоично-десятичной системе запишется в виде 1001 0010 0101. Следует обратить внимание, что эта запись отличается от двоичного изображения данного числа. Например, приведенный выше код в двоичной системе изображает число 2341₁₀.

Дата добавления: 2014-01-07