
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Понятие первообразной функции. Неопределенный интеграл и его свойства
|
|
|
|
Тема 10. Неопределенный интеграл
ЛЕКЦИЯ 11
ПЛАН
1. Понятие первообразной функции. Неопределенный интеграл и его свойства.
2. Таблица основных интегралов.
3. Основные свойства неопределенного интеграла.
4. Метод интегрирования по частям.
5. Метод замены переменной в неопределенном интеграле.
Всякий раз, когда в математике рассматривается какая-либо операция, возникает вопрос об операции, обратной ей. При рассмотрении обратной операции возникает два основных вопроса: ее осуществимость и ее единственность.
После введения операции дифференцирования естественен вопрос об операции, обратной ей, которая называется операцией интегрирования.
Многие задачи естествознания приводят к необходимости отыскания функции по заданной производной этой функции. Например, нахождение закона движения материальной точки по заданной ее скорости или нахождение скорости материальной точки по заданному ее ускорению (которое, согласно второму закону Ньютона, можно определить по действующей на эту точку силе).
Определение 1. Пусть 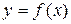 определена на промежутке I. Функция F называется первообразной для функции f на I, если
определена на промежутке I. Функция F называется первообразной для функции f на I, если  для всех
для всех 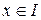 .
.
Так, функция  есть первообразная функции
есть первообразная функции на R.
на R.
С другой стороны, теорема Дарбу (функция 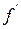 принимает на
принимает на  все значения между
все значения между 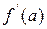 и
и  ) позволяет легко строить примеры функций, которые не имеют первообразных. Далее будет доказано, что всякая непрерывная на отрезке функция имеет первообразную.
) позволяет легко строить примеры функций, которые не имеют первообразных. Далее будет доказано, что всякая непрерывная на отрезке функция имеет первообразную.
Теорема 1. Пусть F - первообразная функции f на I. Тогда:
1) для любого  функция
функция  является первообразной функции f на I;
является первообразной функции f на I;
2) если функция Ф также является первообразной функции f на I, то 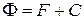 для некоторого числа
для некоторого числа 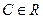 .
.
|
|
|
|
Дата добавления: 2014-01-07; Просмотров: 305; Нарушение авторских прав?; Мы поможем в написании вашей работы!