Интегральный признак сходимости числовых рядов

Теорема 1 (интегральный признак Коши). Пусть - ряд с неотрицательными членами и существует непрерывная, невозрастающая, неотрицательная функция y = f (x), определенная на такая, что f (n) =a_n для всех n Î N. Тогда ряд и несобственный интеграл первого рода 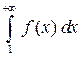сходятся или расходятся одновременно.

Доказательство. Сходимость интеграла 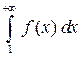функции f, удовлетворяющей условиям теоремы, равносильна существованию предела последовательности, т.е. сходимости ряда

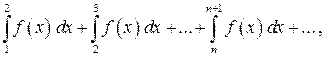
для которого интеграл 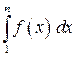является (п- 1)-ой частичной суммой. Осталось показать, что ряды и 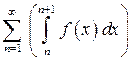сходятся или расходятся одновременно.

В силу монотонности f для любого n Î N при всех x Î[ n; n +1] выполняются неравенства a_{n +1}= f (n +1)£ f (x)£ f (n)= a_n. Следовательно,

для любого n Î N.

Если сходится ряд , то, по признаку сравнения, сходится и ряд с меньшими членами .

Обратно: если сходится ряд , то, по признаку сравнения, сходится и ряд с меньшими членами 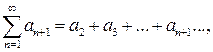. Следовательно, по теореме 2.2, сходится и ряд . Теорема доказана.

Замечание 1. С помощью интегрального признака несложно проверить, что числовой ряд 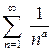сходится, если а >1, и расходится, если a £1. Ряд называется гармоническим рядом, а ряд 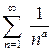с произвольным a Î R называется обобщенным гармоническим рядом.

4. Теорема Лейбница. Абсолютная и условная сходимости рядов

Исследование рядов с членами произвольных знаков представляет более трудную задачу, однако в двух случаях есть удобные признаки: для знакочередующихся рядов - теорема Лейбница; для абсолютно сходящихся рядов применим любой признак исследования рядов с неотрицательными членами.

Определение 1. Числовой ряд называется знакочередующимся, если любые два соседних члена имеют противоположные знаки, т.е. ряд имеет вид или , где a_n >0 для каждого n Î N.

Теорема 1 (Лейбница). Знакочередующийся ряд сходится, если:

1) (a_n) - невозрастающая последовательность;

2) 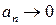при .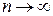

При этом модуль суммы знакочередующегося ряда не превосходит модуля его первого члена, т.е. | S |£ a ₁.

Доказательство. Пусть ряд имеет вид . Рассмотрим последовательность 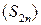. Она является неубывающей, так как для любого n Î N выполняется условие 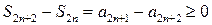, и ограниченной сверху, так как для любого n Î N выполняется условие . Следовательно, последовательность 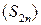сходится. Пусть 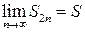. Тогда . Отсюда получаем, что последовательность сходится к S, т.е. ряд сходится и имеет сумму S.

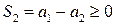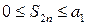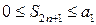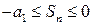Заметим также, что , следовательно, для любого n Î N выполняется условие . Аналогичными рассуждениями доказывается, что , следовательно, . Если же ряд имеет вид , то . Следовательно, в общем случае выполняется неравенство . После предельного перехода при 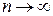получаем , что и требовалось доказать.

Следствие 1. Модуль остатка знакочередующегося ряда типа Лейбница не превосходит модуля его первого члена, т.е. .

Определение 2. Если сходится ряд , то ряд называется абсолютно сходящимся.

Теорема 2. Если сходится ряд , то ряд также сходится.

Например, ряд является абсолютно сходящимися, так как ряд 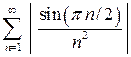сходится по признаку сравнения, ибо 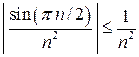для любого n Î N, а ряд 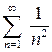сходится (a =2>1).

Абсолютно сходящиеся ряды имеют ряд важных свойств, которыми обладают конечные суммы чисел:

- слагаемые можно переставлять местами;

- слагаемые можно группировать разными способами;

- суммы рядов можно перемножать.

Определение 3. Ряд называется перестановкой ряда , если существует биекция такая, что для любого n Î N.

Теорема 3. Если ряд абсолютно сходится, то сходится, и притом абсолютно, любая перестановка данного ряда, и их суммы совпадают.

Определение 4. Если ряд сходится, а ряд расходится, то ряд называется условно сходящимся.

Ряд является условно сходящимся. Действительно, ряд сходится (по теореме Лейбница), а ряд 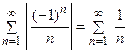расходится.

Теорема 4 (Римана). Если числовой ряд условно сходится, то для любого существует такой числовой ряд , полученный перестановкой членов ряда , что ряд сходится и его сумма равна C.

Дата добавления: 2014-01-07