Уравнения прямых регрессии для парной корреляции

Линейная корреляция.

Основные задачи теории корреляции

Функциональная, статистическая и корреляционная зависимости.

ЛЕКЦИЯ 12

Тема 11: Элементы теории корреляции

ПЛАН

1. Функциональная, статистическая и корреляционная зависимости. Основные задачи теории корреляции.

2. Линейная корреляция. Уравнения прямых регрессии для парной корреляции.

3. Оценка тесноты связи. Коэффициент корреляции (выборочный), его определение и свойства.

4. Коэффициент детерминации и корреляционное отношение.

5. Проверка значимости уравнения регрессии.

"correlatio" – соотношение, взаимосвязь	английские статистики	Ф.Гальтон К.Пирсон	середина XIX века
"regressio" – движение назад

Функциональная зависимость – каждому значению одной переменной соответствует по некоторому правилу единственное значение другой переменной.

Статистическая зависимость – каждому значению одной переменной соответствует множество значений другой переменной. Точнее, каждому значению одной переменной соответствует распределение (условное) другой переменной (стохастическая или вероятностная зависимость).

Например, зависимость урожайности от количества внесенных удобрений.

Определение 1. Корреляционной зависимостью между двумя переменными величинами называется функциональная зависимость между значениями одной из них и условным математическим ожиданием другой.

M_x (Y)=j(x) или M_y (X)=y(y) – уравнения регрессии Y по X или X по Y, функции j(x) и y(y) – функции регрессии, а их графики – линии регрессии.

Для отыскания уравнений регрессии необходимо знать закон распределения двумерной случайной величины (X, Y). На практике, как правило, известна некоторая выборка пар значений (x_i, y_j). Поэтому ставят вопрос об оценке (приближенном выражении) функций регрессии, которую проводят методом наименьших квадратов.

Основные задачи теории корреляции:

– основной задачей регрессионного анализа является установление формы и изучение зависимости между случайными переменными;

– основной задачей корреляционного анализа является выявление связи между случайными переменными и оценка тесноты связи.

Данные о статистической зависимости между двумя переменными величинами удобно задавать в виде корреляционной таблицы:

	y 1	y 2	…	yj	…	ym	Всего: или ni
x 1	n 11	n 12	…	n 1 j	…	n 1 m	n 1
x 2	n 21	n 22	…	n 2 j	…	n 2 m	n 2
…	…	…	…	…	…	…	…
xi	n i1	n i2	…	nij	…	nim	ni
…	…	…	…	…	…	…	…
xl	nl 1	nl 2	…	nlj	…	nlm	nl
Всего: или nj	n 1	n 2	…	nj	…	nm	n

где: l – число интервалов по переменной X, m – число интервалов по переменной Y;

x_i и y_j – середины соответствующих интервалов;

n_ij – частоты пар (x_i; y_j);

, ;

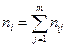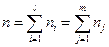– объем выборки.

Определение 1. Корреляционная зависимость между случайными величинами Х и Y называется линейной корреляцией, если обе функции регрессии j(x) и y(y) являются линейными.

Этот вид корреляционной зависимости встречается довольно часто. В этом случае обе линии регрессии являются прямыми и называются прямыми регрессии.

Выведем уравнение прямой регрессии Y по X, т.е. найдем коэффициенты линейной функции j(x)= aх + b.

Для этого применим метод наименьших квадратов, согласно которому неизвестные параметры a и b выбираются так, чтобы была минимальной сумма:

,

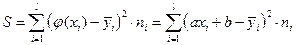где групповые средние 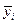вычисляются по формулам:

.

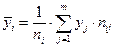Используя необходимое условие экстремума функции двух переменных, получаем систему нормальных уравнений для определения параметров линейной регрессии:

,

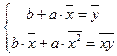где соответствующие средние вычисляются по формулам:

, , , .

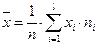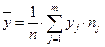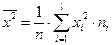Решая систему нормальных уравнений, получаем:

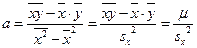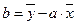, , где:

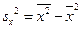– выборочная дисперсия переменной X, – выборочная ковариация.

Коэффициент a в уравнении регрессии называется выборочным коэффициентом регрессии Y по X и обозначается r _yx. Итак,

Аналогично уравнение прямой регрессии X по Y имеет вид 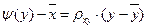, где – выборочный коэффициент регрессии X по Y, показывающий, на сколько единиц в среднем изменяется переменная Х при увеличении переменной Y на одну единицу. Здесь есть выборочная дисперсия переменной Y, где .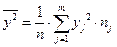

Дата добавления: 2014-01-07