
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Тягово-скоростные свойства и топливная экономичность АТС с гидродинамической трансмиссией
|
|
|
|
ТЕМА
Сведение задач к подзадачам
Goal
Clauses
Predicates
Domains
Пример 5.3.5.
/*Программа: поиск в ширину */
s =symbol
l= s*
ap (l, l, l)
eq (l, l)
udob (l, l, l)
preemn (s, l)
gs(s)
solve (l, l, l) /*Первый аргумент- список отк, второй- зак */
sol
sol:-solve ([s], [], P), write (“sol =”,P),nl.
solve ([X|L1], M, P):- gs(X), P= [X|M].
solve ([X|N], M, P):- M1= [X|M], preemn (X, L), udob (L1, L, L2),
udob (M1, L2, L3), ap(L1, L3,L4), solve (L4,M1, P1), P=P1.
solve ([],M,P):- P= resh.net, write(P),nl.
sol
Она отличается от программы поиска в глубину переменой местами двух первых аргументов предиката ap(L1, L3,L4), что соответствует записи новых вершин в конец списка отк.
Стратегия поиска в ширину гарантирует первоочередную выработку кратчайших решений. Но и поиск в глубину с итеративным углублением с постепенно увеличивающимися пределами глубины, также в первую очередь обнаруживаются кратчайшие решения. Таким образом, при итеративном углублении происходит своего рода моделирование поиска в ширину.
Если в качестве критерия оптимизации рассматривается минимальная стоимость пути решения (а не его длина), поиск в ширину не может обеспечить выбор оптимального пути решения.
Типичной проблемой, связанной с поиском, является комбинаторная сложность. При наличии нетривиальных проблемных областей количество вариантов, подлежащих рассмотрению, становится столь значительным, что наибольшее значение приобретает существенное увеличение затрат ресурсов на исследование данных вариантов.
Сравним затраты ресурсов на осуществление основных алгоритмов поиска. Потребность в ресурсах времени обычно определяется в зависимости от количества узлов, формируемых алгоритмом поиска, а затраты ресурсов пространства обычно определяются в зависимости от максимального количества узлов, которые должны храниться в памяти во время поиска. Общее количество узлов, вплоть до глубины решения d, составляет 0(bd) (см.1), поэтому затраты ресурсов времени при поиске в ширину измеряются значением О(bd ). Кроме того, при поиске в ширину информация обо всех возможных путях хранится в памяти, поэтому затраты ресурсов пространства также измеряются значением О(bd ).
Преимущество поиска в глубину по сравнению с поиском в ширину состоит в том, что он требует намного меньших затрат ресурсов пространства, а его недостатком является то, что он не гарантирует получение оптимального решения.
При итеративном углублении выполняется поиск в глубину (d + 1) со все возрастающей глубиной: 0, 1,..., d. Поэтому затраты ресурсов пространства при этом поиске измеряются значением O(d). Посещение начального узла происходит (d + 1) раз, дочерних узлов начального узла — d раз и т.д. В худшем случае количество формируемых узлов измеряется следующим выражением: (d+l)*l + d*b + (d-l)*b2 +... + l*bd
Это выражение также измеряется значением О(bd). Но фактически затраты на повторное формирование узлов верхних уровней по сравнению с поиском в ширину весьма малы. В этом смысле итеративное углубление сочетает в себе наилучшие свойства поиска в ширину (гарантированное достижение оптимального решения) и поиска в глубину (экономия пространства) и поэтому на практике часто является наиболее предпочтительным среди всех основных методов поиска.
Рассмотренные простые стратегии поиска не имеют средств, позволяющих преодолеть комбинаторный взрыв и поэтому как правило неприменимы для решения крупномасштабных задач. При решении подобных задач необходимо использовать информацию, относящуюся к конкретной проблеме, для обеспечения целенаправленного поиска. Такого рода информация называется эвристикой. Алгоритмы, в которых применяются эвристики, обеспечивают выполнение эвристического поиска. Методы поиска с применением эвристик представлены в следующем пункте.
5.4. Эвристический поиск по заданному критерию: основные понятия; алгоритм А*.
Для многих задач можно сформулировать чисто эмпирические правила, позволяющие уменьшить объем перебора. Все такие правила, используемые для ускорения поиска, зависят от специфической информации о задаче, представляемой в виде графа. Как уже говорилось информацию такого сорта называют эвристической информацией или эвристикой; методы поиска,использующие эвристики, называются эвристическими методами поиска. Один из путей уменьшить перебор состоит в выборе более «информированного» предиката preemn(s,l), который не строит так много не относящихся к делу вершин. Этот способ применим как в методе полного перебора, так и в методе перебора в глубину. Другой путь состоит в использовании эвристической информации для модификации шага (5) алгоритма перебора в глубину. Вместо того чтобы размещать вновь построенные вершины в произвольном порядке в начале списка ОТКРЫТ, их можно расположить в нем некоторым определенным образом, зависящим от эвристической информации. Так, при переборе в глубину в первую очередь будет раскрываться та вершина, которая представляется наилучшей.
Более гибкий (и более дорогой) путь использования эвристической информации состоит в том, чтобы, согласно некоторому критерию,, на каждом шаге переупорядочивать вершины списка" ОТКРЫТ. В этом случае перебор мог бы идти дальше в тех участках границы, которые представляются наиболее перспективными. Для того чтобы применять процедуру упорядочения, необходима мера, которая позволяла бы оценивать «перспективность» вершины. Такие меры называют оценочными функциями.
Как уже отмечалось, обычный способ использования эвристической информации связан с употреблением для упорядочения перебора оценочных функций. Оценочная функция должна обеспечивать возможность ранжирования вершин — кандидатов на раскрытие — с тем, чтобы выделить ту вершину, которая с наибольшей вероятностью находится на лучшем пути к цели. Оценочные функции строились на основе различных соображений. Делались попытки определить вероятность того, что вершина расположена на лучшем пути. Предлагалось также использовать расстояние или другие меры различия между произвольной вершиной и множеством целевых вершин. В салонных играх или головоломках позиции часто ставится в соответствие определенное число очков на основе тех черт, которыми она обладает и которые представляются связанными со степенью уверенности в том, что это шаг к поставленной цели.
Предположим, что задана некоторая функция f, которая могла бы быть использована для упорядочения вершин перед их раскрытием. Через f(n) обозначим значение этой функции на вершине n Условимся располагать вершины, предназначенные для раскрытия, в порядке возрастания их значений функции f. Тогда можно использовать некоторый алгоритм, в котором для очередного раскрытия выбирается та вершина списка ОТКРЫТ, для которой значение f оказывается наименьшим. Будем называть такую процедуру алгоритмом упорядоченного перебора.
Чтобы этот алгоритм упорядоченного перебора был применим для перебора на произвольных графах (а не только на деревьях), необходимо предусмотреть в нем возможность работы в случае построения вершин, которые уже имеются либо в списке ОТКРЫТ, либо в списке ЗАКРЫТ. При использовании некоторой произвольной функции f нужно учесть, что величина f для "некоторой вершины из списка ЗАКРЫТ может понизиться, если к ней найден новый путь (f (n) может зависеть от пути из s к n даже для вершин списка ЗАКРЫТ). Следовательно, мы должны тогда перенести такие вершины назад в список ОТКРЫТ. После принятия этих необходимых мер алгоритм упорядоченного поиска может быть представлен такой последовательностью шагов:
(1) Поместить начальную вершину s в список, называемый
ОТКРЫТ, и вычислить f(s).
(2) Если список ОТКРЫТ пуст, то на выход дается сигнал
о неудаче; в противном случае переходить к следующему этапу.
(3) Взять из списка ОТКРЫТ ту вершину, для которой f имеет наименьшее значение, и поместить ее в список, называемый ЗАКРЫТ. Дать этой вершине имя n. (В случае совпадения значений f для нескольких вершин выбирать вершину с минимальным f произвольно, но всегда отдавая предпочтение целевой вершине.)
(4) Если n— целевая вершина, то на выход подать решающий путь, получаемый прослеживанием соответствующих указателей; в противном случае переходить к следующему этапу.
(5) Раскрыть вершину n, построив все непосредственно следующие за ней вершины. (Если таковых не оказалось, переходить сразу к (2).) Для каждой такой дочерней вершины m
вычислить значение f(m).
(6) Связать с теми из вершин т, которых еще нет в списках
ОТКРЫТ или ЗАКРЫТ, только что подсчитанные значения
f{m). Поместить эти вершины в список ОТКРЫТ и провести
от них к вершине n указатели.
(7) Связать с теми из непосредственно следующих за n вершинами, которые уже были в списках ОТКРЫТ или ЗАКРЫТ, меньшее из прежних и только что вычисленных значений f. Поместить в список ОТКРЫТ те из непосредственно следующих за n вершин, для которых новое значение f оказалось меньше, и изменить направление указателей от всех вершин, для
которых значение f уменьшилось, направив их к n и перейти к п.2.
Отметим, что множество вершин и упомянутых указателей, порождаемых этим алгоритмом, образует дерево (дерево перебора), причем на концах этого дерева расположены вершины из списка ОТКРЫТ.
Работу алгоритма проще всего пояснить, рассмотрев пример игры в восемь. Мы будем пользоваться следующей простой оценочной функцией:
f(n)=g(n)+W(n),
где (п) —длина пути в дереве перебора от начальной вершины до вершины п, a W(n) —это число фишек, которые лежат не на своем месте в описании состояния, связанного с вершиной п.
Так, для начальной вершины
 значение f равно 0 + 4 = 4. По предположению с большей вероятностью на оптимальном пути находится та вершина, которая имеет наименьшую оценку.
значение f равно 0 + 4 = 4. По предположению с большей вероятностью на оптимальном пути находится та вершина, которая имеет наименьшую оценку.
На рис. 5.12. показан результат применения к игре в восемь алгоритма упорядоченного перебора и использования такой оценочной функции. Значение f для каждой вершины приведено внутри кружка. Отдельно стоящие цифры показывают порядок, в котором раскрывались вершины.
Выбор оценочной функции сильно влияет на результат перебора. Использование оценочной функции, не учитывающей истинной перспективности некоторых вершин, может привести к построению путей, не обладающих минимальной стоимостью. С другой стороны, использование оценочной функции, которая

| Рис.5.12.Результат применения алгоритма упорядоченного перебора в игре в восемь(Нильсон,3). |
придает слишком большое значение возможной перспективности всех вершин (такой, как в алгоритме равных цен), приведет к тому, что придется раскрыть очень много вершин. В ниже будет приведен теоретических результат, относящийся к некоторой специальной оценочной функции, использование которой приводит к раскрытию наименьшего числа вершин, совместимого с гарантией нахождения пути минимальной стоимости.
Определим оценочную функцию f так, чтобы значение f (n) для любой вершины n представляло собой сумму оценки стоимости пути минимальной стоимости от начальной вершины s к вершине n и оценки стоимости пути минимальной стоимости от вершины n целевой вершине. Таким образом, f(n) представляет собой оценку стоимости пути минимальной стоимости при условии, что этот путь проходит через вершину п. По этой оценке та вершина списка ОТКРЫТ, которая имеет наименьшее значение f, считается лежащей на пути минимальной стоимости, и поэтому следующей должна быть раскрыта именно она.
Сформированная таким образом функция f дает возможность использовать широко известный алгоритм А*. Предположим, что путь минимальной стоимости от вершины n целевой вершине имеется, и целевым узлом, для которого стоимость этого пути становится минимальной, является узел t. В таком случае оценку f (n) можно сформировать как сумму двух слагаемых (рис.5.12.) следующим образом: f(n)=g(n) + h(n)
где g (n) — оценка стоимости оптимального пути от s до n, a h (п) — оценка стоимости оптимального пути от п до t.
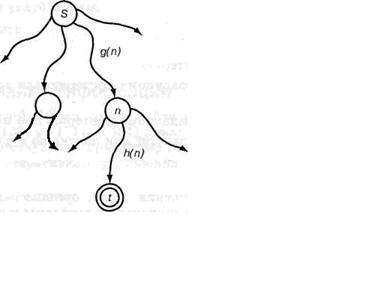
Рис. 5.12. Формирование эвристической оценки f(n) стоимости пути с наименьшей стоимостью от s до t через п:
f(n) = g(n) + h(n)
После обнаружения узла n в процессе поиска возникает следующая ситуация: путь от s до n уже должен быть найден и его стоимость может быть вычислена как сумма стоимости дуг в этом пути. Такой путь от s до n не обязательно должен быть оптимальным (может существовать лучший путь от s до n, еще не обнаруженный в этом процессе поиска), но стоимость найденного пути, выраженная первым слагаемым g (п), может служить в качестве оценки минимальной стоимости пути от s до n. Задача определения второго слагаемого, h(n), сложнее, поскольку множество путей между узлами n и t к этому времени еще не было исследовано в процессе поиска. Поэтому h (n), как правило, представляет собой в полном смысле слова эвристическую гипотезу, основанную на имеющейся в распоряжении алгоритма общей информации о данной конкретной задаче. Поскольку значение h зависит от проблемной области, универсального метода формирования функции h не существует. Предположим, что функция h задана. Алгоритм поиска называется допустимым, если он всегда вырабатывает оптимальное решение (т.е. путь с минимальной стоимостью), при условии, что решение вообще существует. Рассматриваемая здесь реализация, в которой все решения вырабатываются с помощью перебора с возвратами, может считаться допустимой, если оптимальным является первое же из найденных решений. Предположим, что для каждой вершины n в пространстве состояний через h*(n) обозначена стоимость оптимального пути от n до целевого узла.Доказано (см.3), что допустимым является любой алгоритм А*, в котором используется эвристическая функция h, такая, что для всех узлов n в пространстве состояний справедливо следующее утверждение:
h(n) < h*(n). Это предложение имеет большое практическое значение. Даже если неизвестно точное значение h*, достаточно найти нижнюю границу h* и использовать ее в качестве h в алгоритме А*. Это служит достаточной гарантией того, что алгоритм А* выработает оптимальное решение. В частности, может рассматриваться тривиальная нижняя граница, а именно: h(n) = 0 для всех п в пространстве состояний.
Такой вариант действительно гарантирует допустимость. Но недостаток использования условия h = 0 состоит в том, что оно не имеет эвристического потенциала и не обеспечивает какого-либо управления процессом поиска. Алгоритм А*, в котором используется h = 0, ведет себя аналогично алгоритму поиска в ширину. Мало того, он фактически сводит поиск в ширину к такому случаю, что функция стоимости дуг принимает значение с(n, n') = 1 для всех дуг (n,n ') в пространстве состояний. Такое отсутствие эвристического потенциала приводит к значительному увеличению потребности в ресурсах. Поэтому желательно иметь такое значение h, которое является нижним пределом h* (для обеспечения допустимости), а также в максимально возможной степени приближается к h* (для обеспечения эффективности). В идеале, если была бы известна стоимость h*, то в алгоритме можно было бы использовать само значение h*, поскольку алгоритм А*, в котором используется значение h*, находит оптимальное решение непосредственно, вообще без какого-либо перебора с возвратами.
Применение эвристических средств управления поиском по заданному критерию обычно позволяет сократить область поиска таким образом, чтобы в этом процессе посещались только узлы небольшой части пространства состояний задачи. Такое уменьшение области поиска можно рассматривать как сокращение эффективного объема ветвления в процессе поиска. Таким образом, если "среднее" ветвление в про-
странстве состояний задачи равно b, то применение эвристических средств управления поиском фактически приводит к возникновению среднего ветвления b', причем b' обычно значительно меньше чем b.
Несмотря на существенное уменьшение затрат на выполнение поиска, порядок сложности алгоритма А* продолжает оставаться экспоненциально зависимым от глубины поиска. Такое утверждение остается справедливым в отношении потребности в ресурсах и времени, и пространства, поскольку данный алгоритм предусматривает необходимость сопровождения информации обо всех сформированных узлах в памяти. В практических приложениях наиболее важным может стать один из этих ресурсов (время или пространство), и это зависит от конкретных обстоятельств. Но в большинстве практических ситуаций более важным ресурсом является пространство. Алгоритм А* способен за считанные минуты израсходовать все доступное пространство памяти. А после этого поиск фактически не может продолжаться, притом что пользователи часто готовы ждать окончания работы этого алгоритма в течение многих часов или даже суток, поскольку для них весьма важны его результаты.
Разработано несколько вариантов алгоритма А*, позволяющих экономить пространство за счет времени. По своему основному замыслу они аналогичны поиску в глубину с итеративным углублением. Потребность в ресурсах пространства сокращается от экспоненциальной до линейной зависимости от глубины поиска. Но за это приходится платить тем, что в пространстве поиска повторно формируются ранее сформированные узлы.
Один из вариантов модификации алгоритма А* называется IDA*- Iterative Deepening A* (алгоритм А* с итеративным углублением).
Метод IDA* аналогичен поиску в глубину с итеративным углублением, за исключением описанного ниже отличия. При итеративном углублении поиск в глубину осуществляется со все возрастающими пределами глубины. При каждой итерации поиск в глубину ограничивается текущим пределом глубины. Но в методе IDA* последовательный поиск в глубину ограничивается текущим пределом значений оценок узлов (т.е. эвристических f-значений узлов). Поэтому основной механизм поиска в методе IDA* также основан на поиске в глубину, при котором потребность в ресурсах пространства является очень низкой.
. При решении крупных задач поиска экономия пространства, достигаемая с помощью метода IDA*, может оказаться весьма значительной, тогда как издержки, связанные с повторением поиска, остаются вполне приемлемыми. Величина этих издержек зависит от свойств пространства поиска, в частности от свойств функции оценки f. В благоприятных ситуациях многие узлы имеют равные f-значения. В подобных ситуациях на каждом очередном этапе поиска в глубину рассматривается много новых узлов, количество которых превышает количество повторно формируемых узлов. Поэтому дополнительные издержки сравнительно малы. В неблагоприятных ситуациях f-значения, как правило, не являются одинаковыми для многих узлов. В крайнем случае каждый узел может иметь отличное от других f-значение. При этом возникает необходимость использовать целый ряд последовательных f-пределов, когда при каждом новом поиске в глубину формируется только один новый узел, а все остальные узлы представляют собой повторно сформированные узлы (которые были сформированы на предыдущих этапах и удалены из памяти). В таких крайних случаях дополнительные издержки, связанные с использованием метода IDA*, действительно становятся неприемлемыми.
Еще одно интересное свойство метода IDA* касается допустимости. Предположим, что функция f (N) определена как g(N) + h(N) для всех узлов N. Если функция h является допустимой (т.е. h(N) < h* (N) для всех N), то метод IDA* гарантирует нахождение оптимального решения.
Одним из возможных недостатков метода IDA* является то, что он не обеспечивает исследование узлов в порядке оценок по заданному критерию (т.е. в порядке возрастания f-значений). Например, предположим, что f — это функция оценки, которая не обязательно представлена в форме f = g + h. Если функция f не монотонна, то упорядочение по заданному критерию не гарантируется. Функция f называется монотонной, если ее значение монотонно возрастает вдоль путей в пространстве состояний. Причина нарушения упорядоченности по заданному критерию состоит в том, что при использовании немонотонной функции f значение f-предела может стать настолько большим, что узлы с разными f-значениями будут впервые развертываться при этом поиске в глубину. Процедура поиска в глубину будет развертывать узлы до тех пор, пока для них значение функции f не превысит f-предела, без учета того, в каком порядке они развертываются.
В этом пункте рассматривается подход к решению задач, основанный на сведении задачи к подзадачам. Идея такого подхода состоит «в размышлении в обратном направлении» от задачи, которую предстоит решить, с тем чтобы выделить подзадачи, подподзадачи и т. д., пока, наконец, первоначальная задача не будет сведена к набору тривиальных элементарных задач. Графы AND/OR могут служить удобным средством представления тех задач, которые возможно естественным образом разложить на ряд взаимно независимых подзадач. К примерам таких задач относится поиск маршрута, проектирование, символическое интегрирование, игры, доказательство теорем и т.д.
5.5.1. Представление задач в виде графов AND/OR
Выше рассматривались способы решения задач, представленных с помощью пространства состояний. В соответствии с этим решение задачи сводилось к поиску пути в графе пространства состояний. Но для некоторых категорий задач более естественно подходит другое представление, в виде графа AND/OR. Графы AND/OR могут служить удобным средством представления тех задач, которые возможно естественным образом разложить на ряд взаимно независимых подзадач. К примерам таких задач относится поиск маршрута, проектирование, символическое интегрирование, игры, доказательство теорем и т.д.
В основе такого представления лежит декомпозиция задачи на подзадачи. Декомпозиция на подзадачи может применяться, если подзадачи являются взаимно независимыми и поэтому могут решаться независимо друг от друга.
Проиллюстрируем сказанное выше на примере(см.1). Рассмотрим задачу поиска маршрута между двумя указанными городами на дорожной карте, показанной на рис. 5.13. На данный момент значения длины маршрутов будут игнорироваться. Эту задачу, безусловно, можно сформулировать как поиск пути в пространстве состояний. Соответствующее пространство состояний может выглядеть полностью аналогично этой карте: узлы в пространстве состояний соответствуют городам, дуги — прямым соединениям между городами, а стоимости дуг — расстояниям между городами. Но может рассматриваться и другое представление этой задачи, основанное на ее естественной декомпозиции.
На карте, приведенной на рис.5.13, имеется также река. Предположим, что эту реку можно пересечь только с помощью двух мостов, один из которых находится в городе f, а другой — в городе д. Очевидно, что необходимо включить в разрабатываемый маршрут один из мостов, поэтому маршрут должен пройти или через f, или через д. Таким образом, имеются два описанных ниже основных варианта.
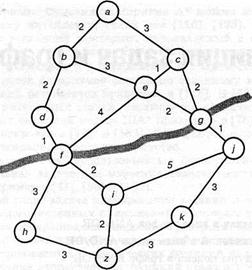
Рис.5.13. Поиск маршрута между городами a и z no дорожной карте. Реку можно пересечь е пункте f или д. Представление этой задачи в виде графа AND/OR показано на рис. 5.14.(Братко,1).
Чтобы найти путь от а до z, необходимо выполнить одно из следующих действий.
1. Найти путь от а до z через f.
2. Найти путь от а до z через д.
Теперь каждый из этих двух вариантов задачи можно разложить на подзадачи, как описано ниже.
1. Чтобы найти путь от а до z через f, необходимо выполнить следующее:
1.1.найти путь от а до f;
1.2.найти путь от f до z.
2. Чтобы найти путь от а до z через д, необходимо выполнить следующее:
2.1. найти путь от а до д;
2.2. найти путь от д до z.
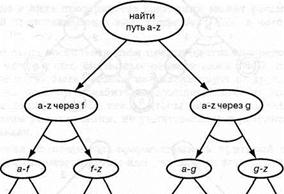
В конечном итоге имеются два основных варианта решения первоначальной задачи: проложить маршрут через f или проложить его через д. Кроме того, каждый из этих вариантов задачи можно разделить на две подзадачи (соответственно, 1.1 и 1.2 или 2.1 и 2.2). Здесь важно то, что (в обоих вариантах) каждая из подзадач может быть решена независимо от другой. Такую декомпозицию можно представить в виде графа AND/OR (рис.5.14). Обратите внимание на две дуги, соединенные кривой линией, которые обозначают связь AND между подзадачами. Безусловно, что граф, показанный на рис.5.14, представляет собой только верхнюю часть соответствующего дерева AND/OR. Дальнейшая декомпозиция подзадач может быть основана на рассмотрении других промежуточных городов.
Какими являются целевые узлы в подобном графе AND/OR? Целевые узлы соответствуют подзадачам, которые являются тривиальными, или "простейшими". В данном примере такой подзадачей будет "поиск маршрута от а до с", поскольку на дорожной карте имеется прямое соединение между городами а и с.
В этом примере введены некоторые важные понятия. Граф AND/OR представляет собой ориентированный граф, узлы которого соответствуют задачам, а дуги обозна-
|
чают отношения между задачами. Имеются также отношения между самими дугами. Этими отношениями являются AND и OR, в зависимости от того, требуется ли решить только одну из задач-преемников или сразу несколько. В принципе, из любого узла могут исходить и дуги, связанные отношением AND, и дуги, связанные отношением OR. Но мы предполагаем, что каждый узел имеет либо только преемников AND, либо только преемников OR. Дело в том, что каждый граф AND/OR можно преобразовать в стандартную форму, введя по мере необходимости вспомогательные узлы OR. Поэтому узел, из которого исходят только дуги AND, называется узлом AND, а узел, из которого исходят только дуги OR, называется узлом OR.
Рис.5.14. Представление задачи поиска маршрута, приведенной на рис 5.13, в виде графа AND/OR. Узлы соответствуют задачам или подзадачам, а дуги, соединенные кривыми, показывают, что должны быть решены все (в данном случае обе) подзадачи
|
|
| б) |
|
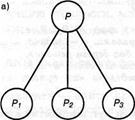
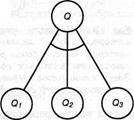
Рис.5.15. Два типа узлов в графе AND /OR: а) чтобы решить задачу Р, достаточно решить любую из подзадач PI, P2 или...; б) чтобы решить задачу Q, необходимо решить все подзадачи, и Q1, и Q2, и...
В представлении в виде пространства состояний решение задачи сводилось к поиску пути в пространстве состояний. Каково же решение в представлении в виде графа AND/OR? Безусловно, что любое решение должно включить все подзадачи любого узла AND. Поэтому теперь решение является не путем, а деревом. Такое дерево решения, Т, определяется следующим образом.
■ Первоначальная проблема, Р, является корневым узлом дерева Т.
■ Если Р — узел OR, то в дереве Т находится один и только один из его преем
ников (по графу AND/OR) вместе с его собственным деревом решения.
■ Если Р — узел AND, то в дереве Т находятся все его преемники (по графу
AND/OR) наряду с их деревьями решения.
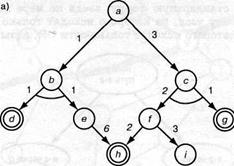
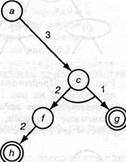
Это определение показано на рис.5.15. На данном рисунке показаны также стоимости, назначенные дугам. Стоимости позволяют сформулировать критерий оптимизации. Можно, например, определить стоимость графа решения как сумму всех стоимостей дуг в этом графе. Поскольку нас обычно интересует минимальная стоимость, то предпочтительным является граф решения, показанный на рис.5.16, в.

|
|
| в) |
| б) |
Рис.5.16.. Примеры графов решения: а) граф AND /OR, в котором d, g и h являются целевыми узлами, a — задача, которая должна быть решена; б) и в) два дерева решения, стоимость которых составляет соответственно 9 и 8. Здесь стоимость дерева решения определена как сумма всех стоимостей дуг в дереве решения
Но мы не обязаны всегда рассматривать стоимости дуг в качестве критерия оптимизации. Иногда более естественно связать стоимости с узлами, а не с дугами или связать их и с дугами, и с узлами.
На основании сказанного выше можно сделать следующие выводы.
■ Представление задачи в виде графа AND/OR основано на принципе декомпозиции задачи на подзадачи.
■ Узлы в графе AND/OR соответствуют задачам, а связи между узлами указывают на отношения между задачами.
Узел, из которого исходят связи OR, представляет собой узел OR. Для решения задачи, обозначенной узлом OR,достаточно решить одну из задач его узлов-преемников.
Узел, из которого исходят связи AND, представляет собой узел AND. Для решения задачи, обозначенной узлом AND, необходимо решить все задачи его узлов-преемников.
Для указанного графа AND/OR конкретная задача формулируется с помощью следующих двух понятий:
начальный узел;
целевое условие для распознавания целевых узлов.
■ Целевые (или "оконечные") узлы соответствуют тривиальным (или "простейшим") задачам.
■ Любое решение представлено в виде графа решения, который является подграфом графа AND/OR.
■ Представление в виде пространства состояний может рассматриваться как частный случай представления в виде графа AND/OR, в котором все узлы являются узлами OR.
■ Чтобы можно было воспользоваться преимуществами представления AND/OR,необходимо, чтобы узлы, связанные отношениями AND, представляли подзадачи, которые могут быть решены независимо друг от друга. Критерий независимости можно немного ослабить следующим образом: должно существовать упорядочение подзадач AND, такое, чтобы решения подзадач, встречающихся раньше при этом упорядочении, не уничтожались в результате решения последующих подзадач.
■ Для обеспечения возможности сформулировать критерий оптимизации могут
быть назначены стоимости дугам или узлам, или тем и другим.
5.5.2. Примеры представлений в виде графа AND/OR
Пример 5.5.1. Представление в виде графа AND/OR задачи поиска маршрута
Для задачи поиска кратчайшего маршрута (см. рис.5.13) граф AND/OR, который включает функцию стоимости, можно определить следующим образом.
■ Узлы OR имеют форму X-Z, а это означает, что нужно найти кратчайший
маршрут от X до Z.
■ Узлы AND имеют такую форму:
X-Z via Y
а это означает — найти кратчайший маршрут от X до Z, при условии, что этот маршрут должен пройти через Y.
■ Узел X-Z является целевым узлом (простейшая задача), если X и Z на карте со
единены непосредственно.
■ Стоимость каждого целевого узла X-Z представляет собой указанное дорожное
расстояние между X и Z.
■ Стоимости всех других (нетерминальных) узлов равны 0.
Стоимость графа решения представляет собой сумму стоимостей всех узлов в графе решения (в данном случае это сумма стоимостей всех терминальных узлов). Для задачи, показанной на рис.5.13, начальным узлом является a-z. На рис. 5.17.показано дерево решения со стоимостью 9. Это дерево соответствует маршруту [a,b,d,f,i,z], который можно реконструировать из дерева решения, посетив все листья в этом дереве в последовательности слева направо.
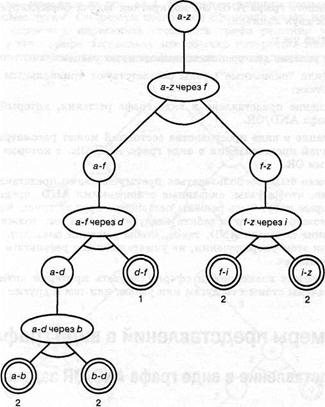
Рис.5.17. Дерево решения с минимальной стоимостью для задачи поиска маршрута (см. рис.5.13.), оформленное в виде графа AND /OR
Пример 5.5.2. Задача с ханойской башней
Задача с ханойской башней (рис.5.18) является еще одним классическим примером эффективного применения схемы декомпозиции AND/OR. Для упрощения рассмотрим описанную ниже простую версию этой задачи, содержащую только три диска.
Даны три оси, 1, 2 и 3, и три диска, а, bи с (из них а — самый маленький и с — самый большой). Первоначально все диски нанизаны на ось 1. Задача состоит в том, чтобы перенести их все на ось 3. Разрешено переносить одновременно только один диск и нельзя класть диск большего диаметра на диск меньшего диаметра.
|
Рис.5.18. Задача с ханойской башней
Такую задачу можно рассматривать как задачу достижения следующего множества целей.
1. Диск а на оси 3.
2. Диск b на оси 3.
3. Диск с на оси 3.
К сожалению, эти цели не являются независимыми. Например, диск а можно немедленно нанизать на ось 3, достигнув первой цели. Но это помешает достижению двух других целей (если мы не откажемся от непосредственного достижения первой цели). К счастью, имеется удобный способ упорядочения процесса достижения этих целей, такой, что решение можно легко найти на основании этого упорядочения. Требуемую последовательность достижения всех целей можно определить с помощью следующих рассуждений: цели 3 (диск с на оси 3) достичь сложнее всего, поскольку для перемещения диска с необходимо преодолеть больше всего ограничений. Хорошая идея, которая часто оказывается продуктивной в подобных ситуациях, состоит в том, что вначале следует попытаться достичь самой сложной цели. В основе этого принципа лежит наблюдение, что если другие цели не являются такими труднодостижимыми (не связаны с преодолением таких ограничений, как самая трудная), то можно надеяться, что их удастся достичь без необходимости отмены результатов достижения этой самой трудной цели.
Таким образом, стратегия решения задачи, которая вытекает из этого принципа, состоит в следующем:
вначале достичь цели "диск с на оси 3"; затем достичь оставшихся целей.
Но первой из этих целей нельзя достичь немедленно: в начальной ситуации диск с невозможно переместить сразу же, поскольку на нем лежат еще два диска. Поэтому вначале подготовим этот ход и уточним нашу стратегию следующим образом.
1. Обеспечить перемещение с оси 1 на ось 3 диска с.
2. Перенести с оси 1 на ось 3 диск с.
3. Достичь оставшихся целей — диск а на оси 3 и диск b на оси 3.
Диск с можно перенести с оси 1 на ось 3, если оба оставшихся диска, а и b, нанизаны на ось 2. Поэтому наша первоначальная задача переноса с оси 1 на ось 3 дисков a, b и с сводится к трем перечисленным ниже подзадачам.
Чтобы переместить с оси 1 на ось 3 диски а, b и с, необходимо выполнить следующее.
1. Переместить с оси 1 на ось 2 диски а и b.
2. Переместить с оси 1 на ось 3 диск с.
3. Переместить с оси 2 на ось 3 диски а и b.
Задача 2 является тривиальной (решение состоит из одного хода). Две другие подзадачи можно решить независимо от задачи 2, поскольку диски а и b можно переносить независимо от положения диска с. Чтобы решить задачи 1 и 3, можно применить тот же принцип декомпозиции (на этот раз самой сложной является задача перемещения диска b). В соответствии с этим задача 1 сводится к трем перечисленным ниже тривиальным подзадачам.
Чтобы переместить с оси 1 на ось 2 диски а и Ь, необходимо выполнить следующее.
1. Переместить с оси 1 на ось 3 диск а.
2. Переместить с оси 1 на ось 2 диск b.
3. Переместить с оси 3 на ось 2 диск а.
В заключение отметим, что многие игры такие, например, как шахматы и шашки, могут быть естественным образом представленные в виде графов AND/OR. (см.1).В 1.-3. можно найти описание процедур поиска на AND/OR графах с реализацией их на языке Пролог (см.1).
5.6. Упражнения.
1. Приведите примеры следующих графов:
1.1. Граф,имеющий петли и параллельные ребра;
1.2. Корневой граф, имеющий циклы;
1.3. Корневой ациклический граф, не являющийся деревом;
1.4. Граф- дерево, не являющееся корневым графом.
2. Выберите схему расположения пяти городов с указанием разметки (расстояний между городами или стоимостей переездов из города в город); постройте пространство состояний для задачи коммивояжера с такой схемой городов; укажите путь в графе, представляющий решение задачи.
3. Представьте в пространстве состояний известную задачу о переправе через реку человека, волка, козы и капусты.
4. Пройдите «вручную» алгоритм с возвратами для выбранного Вами корневого графа на 15 вершинах, имеющего хотя бы один цикл.
5. Составьте программу на языке Турбо- Пролог, реализующую алгоритм поиска с возвратами на Вашем графе из п. 4.
6. Постройте дерево эвристического поиска для игры в «8» с начальными позициями
а). 1 3 4 б). 2 1 6
8 2 4 8
7 6 5 7 5 3,
используя оценочную функцию, определенную в п.; предложите свой вариант оценочной функции и примените его в этой задаче.
7. Приведите пример задачи, допускающей естественную декомпозицию на подзадачи и укажите ее представление графом AND/OR.
8. Постройте граф состояний для задачи о ханойской пирамиде, представляя состояния упорядоченной тройкой чисел из набора
{1, 2,3}.
9. Постройте граф состояний для известной задачи о кувшинах: имеются два кувшина вместимостью 8 и 5 литров и бочка
с жидкостью. Как, использую только указанные емкости, отмерить 4л?
10*. Из доски, содержащей 2n x 2n клеток вырезано по одной клетке из двух противолежащих (по диагонали) углов. Докажите, что теперь доску невозможно покрыть полностью фишками размером 1х2 так, чтобы они не высовывались за край доски и не накрывали друг друга.
Указание: Удалите из доски по одной клетке из двух ее противолежащих углов. Покажите, что теперь невозможно полностью покрыть эту искаженную доску фишками размером 1´2 так, чтобы они не высовывались за край доски и не накрывали друг друга. Рекомендуем рассмотреть сначала частные случаи доски: 2´2, 4´4, 8´8 и лишь потом перейти к общему случаю.
11*. На каком-нибудь процедурном языке программирования разработайте программу поиска решений в игре в «8».
12*. На языке Турбо-Пролог разработайте программу реализующую алгоритм решения задачи «Обезьяна и бананы».
13*. На каком-нибудь процедурном языке разработайте программу:
13.1. Поиск в глубину в пространстве состояний;
13.2. Поиск в ширину;
13.3 Поиск с применением эвристик.
14.Напишите на языке Турбо-Пролог программу, перемещающую в задаче «Ханойские башни» N дисков с левого стержня на правый.
Литература
1. И. Братко.Алгоритмы искусственного интеллекта на языке PROLOG. М.: ВИЛЬЯМС,2004.
2. Д. Ф. Люггер. ИСКУССТВЕННЫЙ ИНТЕЛЛЕКТ, М.-СПб.-К. ВИЛЬЯМС,2003.
3. Н. Нильсон. ИСКУССТВЕННЫЙ ИНТЕЛЛЕКТ,М.: МИР,1973.
4. Н. Ф. Мануилов. ИСКУССТВЕННЫЙ ИНТЕЛЛЕКТ, Смоленск, УНИВЕРСУМ, 2005.
Топливная экономичность АТС
Основные определения. Топливная характеристика при установившемся движении. Экспериментальное определение топливной характеристики. Расчетная формула определения удельного расхода топлива (Ур-е расхода топлива). Расход топлива на различных передачах. Контрольный расход топлива. Топливная характеристика циклического движения. Влияние конструктивных и эксплуатационных (обтекаемость, сопротивление дороги) факторов на топливную экономичность АТС. Потери мощности ДВС: термодинамические и механические, затраты на привод вспомогательных агрегатов. Выбор параметров трансмиссии. Техническое состояние АТС. Квалификация водителя.
Топливная экономичность – совокупность свойств, определяющих расход топлива при выполнении транспортных работ в различных условиях эксплуатации.
Основным измерителем топливной экономичности в большинстве европейских стран является расход топлива в литрах на 100км пути (путевой расход) - Qs. Qw- расход топлива на единицу выполненной работы. В США используют обратную величину пробега на единицу объема израсходованного топлива.
В соответствие ГОСТ 20306 оценочными показателями топливной экономичности служат:
1. Контрольный расход топлива (КРТ) – определяют для всех категорий АТС при заданных значениях скорости движения при движении по прямой горизонтальной дороге на высшей передаче.
2. Расход топлива в магистральном ездовом цикле на дороге (РТМЦ) – измеряют для всех АТС, кроме городских автобусов, пробегом по измерительному участку с соблюдением режимов движения, заданных определенной картой и схемой цикла (рис. 56.)

3. Расход топлива в городском ездовом цикле на дороге (РТГЦд) – оценивают для всех АТС, кроме магистральных автопоездов, междугородных и туристических автобусов, пробегом по измерительному участку с соблюдением режимов движения, заданных определенной картой и схемой цикла.
 4. Расход топлива в городском ездовом цикле на стенде (РТГЦ) – определяют только для АТС, у которых масса менее 3,5 т, испытанием на стенде с беговыми барабанами по ездовому циклу в соответствие с операционной картой и схемой цикла.
4. Расход топлива в городском ездовом цикле на стенде (РТГЦ) – определяют только для АТС, у которых масса менее 3,5 т, испытанием на стенде с беговыми барабанами по ездовому циклу в соответствие с операционной картой и схемой цикла.
5. Топливная характеристика установившегося движения (ТХ) – график зависимости расхода топлива Qs от скорости установившегося движения на высшей передаче по горизонтальной дороге(рис.57).
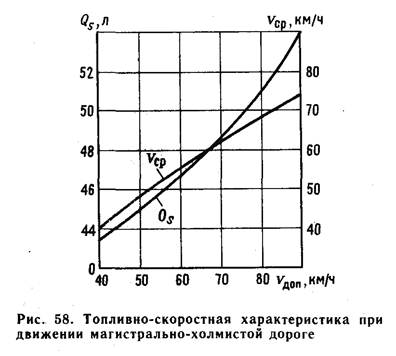
6. Топливно – скоростная характеристика на магистрально – холмистой дороге (ТСХ) – график (рис. ТСХ) зависимости расхода топлива Qs и скорости Vср от Vдоп при движении по магистрально – холмистой дороге с заданным продольным профилем. Характеризует магистральные автопоезда, междугородние и туристические автобусы.
Уравнение расхода топлива
Удельный расход топлива gе=1000Qт/Nе, где Qт – часовой расход топлива.
Qт=gе·Nе/1000= gе·Nт/(1000ηтр) = gе·(Nд + Nв+ Nи) /(1000ηтр)=gе·V· (Fд+Fв+Fи) /ηтр, учитывая, что Qs=1000·Qт/(36·V·ρт), где ρт – плотность топлива, кг/л, получим, что
Qs =1000· gе·(Nд +Nв+Nи)/(1000ηтр·36·V·ρт)= gе·(Nд+Nв+Nи)/(36·V·ρт ηтр)=
= gе·(Fд+Fв+Fи) /(36000·ρт·ηтр) – уравнение расхода топлива, откуда
gе= 36000 Qs ·ρт·ηтр /(Fд+Fв+Fи) или gе= 36·Qs·V·ρт·ηтр/(Nд+Nв+Nи)
Можно также пользоваться эмпиричеческой зависимостью, выведенной И.С.Шлиппе:
gе=gNkиkч, где
gN – удельный расход топлива при Nемах;
kи – коэффициент, учитывающий загрузку ДВС по мощности;
kч - коэффициент, учитывающий загрузку ДВС по частоте вращения.
Топливно – экономическая характеристика
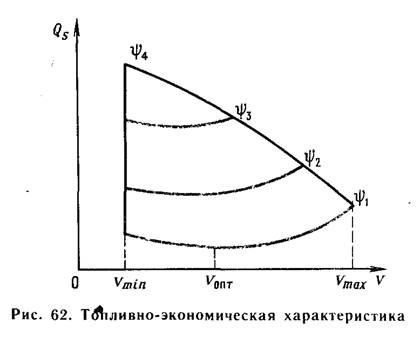 Для анализа связи расхода топлива с условиями движения Е.А.Чудаковым предложен график: топливно – экономическая характе-ристика (рис.62) (ψ – суммарный коэффициент дорожного сопротивления), которая может быть построена по результатам дорожных или стендовых испытаний, при этом семейство кривых Qs=f(v) слева ограничивается линией, соединяющей точки минимально – устойчивых скоростей движения, справа и сверху топливно – экономическая характеристика ограничивается огибающей кривой, соответствующей расходам топлива при 100% загрузке ДВС.
Для анализа связи расхода топлива с условиями движения Е.А.Чудаковым предложен график: топливно – экономическая характе-ристика (рис.62) (ψ – суммарный коэффициент дорожного сопротивления), которая может быть построена по результатам дорожных или стендовых испытаний, при этом семейство кривых Qs=f(v) слева ограничивается линией, соединяющей точки минимально – устойчивых скоростей движения, справа и сверху топливно – экономическая характеристика ограничивается огибающей кривой, соответствующей расходам топлива при 100% загрузке ДВС.
Для дизелей gемин=190…230 г/кВтч, для ДВС с ИСЗ – 250…310 г/кВтч.
Влияние конструктивных факторов на топливную экономичность.
1 Дизелизация АТС (но габариты, масса, шумность).
2 Степень сжатия.
3 Системы впрыска топлива.
4 МПСУ.
5 Наддув и промохлаждение.
6 Отключение вентилятора.
7 Снижение мехпотерь.
8 Адиабатизация.
9 Бесступенчатость трансмиссии.
10 Масса АТС.
11 Аэродинамика (обтекаемость).
12 Качество и геометрия шин (снижение f).
Это может обеспечить в общем повышение экономичности на
15…20 %
Влияние эксплуатационныхфакторов на топливную экономичность.
1Коэффициент загрузки АТС (автопоезда, большая вместимость автобуса).
2 Профессионализм водителя.
3 Минимизация режимов торможения и разгона.
4 Техническое состояние АТС:
- двигатель, его регулировки, качества и соответствие ГСМ;
- сцепление, выжимной механизм;
- КПП, раздаточные коробки;
- карданные передачи;
- главная передача, редуктор, дифференциал.
5 Сопротивление дороги, ее качество.
ТЕМА:
Исходные характеристики гидропередач. Совместная работа ДВС и гидропере-дачи. Способы улучшения преобразующих и энергетических свойств гидропередач. Динамическая характеристика и параметры приемистости автомобиля с гидро-трнсмиссией. Расход топлива АТС с гидротрансмиссией.
Непрерывное увеличение динамики АТС и интенсивности движения на дорогах, крайне отрицательно сказывается на напряженности труда водителя и, как следствие, ведет к снижению безопасности движения. Во избежание последнего, одним из наиболее эффективных мероприятий является автоматизация управлением автомобиля и в частности применение (бесступенчатых) автоматических и п/автоматических трансмиссий. В основе таких трансмиссий лежат гидромеханические передачи, состоящие из гидромуфты или гидротрансформатора и механического вального или планетарного редуктора.
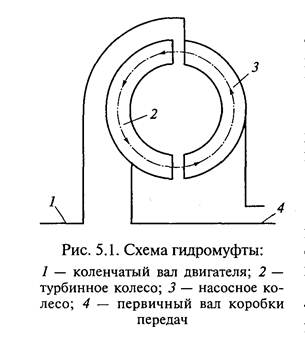
Гидродинамическая муфта состоит из турбинного колеса, насосного и сочлененного с ним кожуха. В идеале между крутящими моментами турбины и насоса устанавливается соотношение: Mт = Mн что означает, что коэффициент трансформации μ= Mт / Mн =1 и ηгидр= iгм, в действительности iгм = 0,95…0,98 при движении по автостраде, а в обычных условиях эксплуатации он еще меньше, так как существует эффект проскальзывания колес относительно друг друга.
Вследствие наличия скольжения кривая крутящего момента скоростной характеристики двигателя при наличии гидромуфты смещается в область меньших угловых скоростей коленчатого вала. На рис. 5.2 представлена тяговая характеристика автомобиля с гидромуфтой. для сравнения штриховыми линиями на рисунке приведена тяговая характеристика автомобиля без гидромуфты. Следовательно, гидромуфта позволяет использовать большое значение крутящего момента двигателя в начале разгона или при движении с очень малой скоростью. Это обеспечивает плавное трогание автомобиля с места на любой передаче и исключает прекращение работы двигателя при остановке автомобиля с невыключенным сцеплением. Из рисунка видно, что тягово-скоростные свойства автомобиля при наличии гидромуфты изменяются только в области малых значений угловой скорости коленчатого вала и во время трогания автомобилей с гидромуфтой автомобиля с места.

ЛЕКЦИЯ 11
Этого недостатка лишен гидротрансформатор, в состав которого включен реактор, что позволяет ему работать в двух режимах: при отсутствии значительных сопротивлений в трансмиссии ГТР работает как обычная ГМ, а при увеличении сопротивления в трансмиссии включается в работу реактор или иначе - автолог, сочленяющийся с валом насоса посредством обгонной муфты.
Коэффициент трансформации момента μ= Mт / Mн возрастает в функции отношения частот вращения насосного и турбинного колес. Максимальное увеличение момента достигается при iгтр = 0, т. е. при остановленной турбине (стоп-режим). Повышение частоты вращения турбины фактически сопровождается линейным уменьшением коэффициента трансформации до тех пор, пока не достигается режим с соотношением моментов 1:1. Реактор, связанный с кожухом ГТР через механизм свободного хода начинает вращаться в потоке рабочей жидкости.

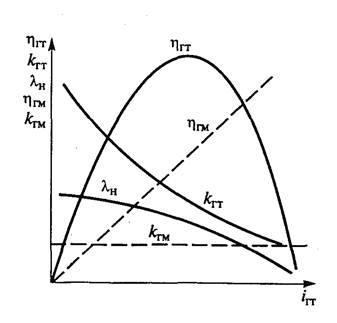

Геометрия лопастей и их пространственное размещение выбирается таким образом, чтобы обеспечивался коэффициент трансформации 1,9…2,5 на стоп-режиме Кривая гидравлического к.п.д. ηгид = iгтрμ в диапазоне преобразований близка к параболической. За режимом ГМ, который характеризуется скольжением 10…15%, η соответствует iгтр и достигает 97% при высоких угловых скоростях ДВС.
В тяговом режиме угловая скорость турбинного колеса ωт ниже угловой скорости насосного колеса ωн по причине наличия проскальзывания турбинного колеса относительно насосного, передаточное отношение (число) при этом будет равно iгтр= nт /nн= ωт/ωн, кроме того, кинематические свойства можно характеризовать скольжением в % s=100(ωн- ωт)/ ωн=100(1- iгтр).
Энергетические свойства гидропередачи характеризуются КПД, равным
ηгтр=Nт/Nн= Мтωт/(Мнωн)=μ·iгтр
Т.к. для ГМ μ=1, то ηгм=iгм. График зависимости μ и ηгм от iгм называют исходной (безразмерной) характеристикой гидропередачи.
У гидротрансформатора зависимость μ=f(iгтр) близка к параболической.
Способность ГТР передавать изменение сопротивления движению ведущему валу и тем самым изменять режим работы двигателя при неизменном положении дросселя условно называется прозрачностью.
Гидротрансформатор устанавливают в трансмиссии автомобиля обычно совместно с планетарной коробкой передач.
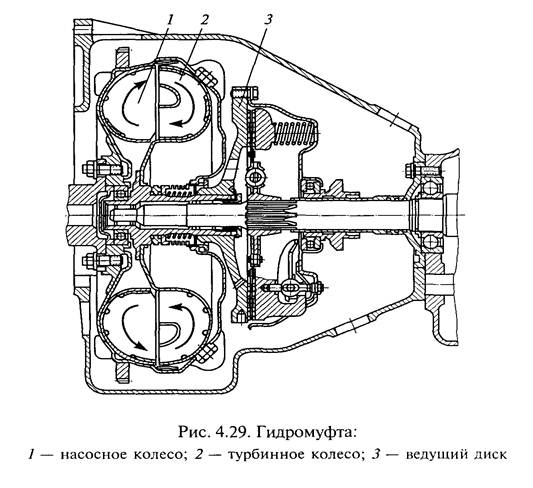
Ведущая часть гидротрансформатора (рис. 5.3) — насос 2, жестко соединенный с коленчатым валом 6 двигателя, а ведомая часть — турбина 1 — с валом трансмиссии 3. Между насосом и турбгидротрансформатора на муфте свободного хода 4 установлен реактор 5, обеспечивающий плавный и безударный вход масла из турбины в насос и существенное увеличение передаваемого крутящего момента.
|
|
|
|
Дата добавления: 2014-01-07; Просмотров: 629; Нарушение авторских прав?; Мы поможем в написании вашей работы!