
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Проекции вектора на ось
|
|
|
|
Определение. Проекцией точки  на ось
на ось 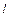 в направлении проектирующей плоскости
в направлении проектирующей плоскости 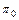 (проектирующей прямой
(проектирующей прямой 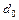 ) называют точку
) называют точку 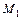 пересечения оси
пересечения оси 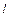 с плоскостью
с плоскостью 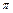 (с прямой
(с прямой 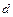 ), проходящей через точку
), проходящей через точку  параллельно плоскости
параллельно плоскости 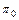 (прямой
(прямой 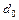 ).
).

Определение. Векторной проекцией вектора  на ось
на ось 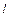 называют вектор
называют вектор 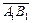 оси
оси 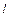 , для которого точка
, для которого точка  есть проекция точки
есть проекция точки  , точка
, точка 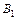 есть проекция точки
есть проекция точки 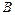 на эту же ось:
на эту же ось:
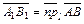 . (7.1)
. (7.1)
Определение. Скалярной проекцией вектора  на ось
на ось 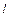 называют число
называют число 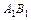 , абсолютная величина которого равна модулю векторной проекции
, абсолютная величина которого равна модулю векторной проекции 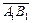 вектора
вектора  на ось
на ось 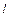 , причем
, причем 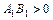 , если направление вектора
, если направление вектора 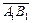 совпадает с направлением оси
совпадает с направлением оси 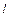 , и
, и 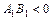 в противном случае.
в противном случае.
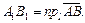 (7.2)
(7.2)
Нетрудно показать, что векторная и скалярная проекции вектора на ось связаны соотношением
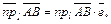 . (7.3)
. (7.3)
Теорема 7.1. Проекциясуммы двух векторов на какую-либо ось равна сумме проекций векторов-слагаемых на эту же ось.
Замечание. Утверждение теоремы справедливо как для векторных проекций, так и для скалярных:
 , (7.4)
, (7.4)
 . (7.5)
. (7.5)
Теорема 7.2. Проекция произведения вектора на число на какую-либо ось равна произведению этого числа на проекцию данного вектора на эту же ось:
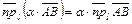 , (7.6)
, (7.6)
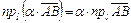 . (7.7)
. (7.7)
Следствие. Проекция на какую-либо ось линейной комбинации векторов равна точно такой же линейной комбинации (с теми же самыми коэффициентами) проекций на эту же ось векторов линейной комбинации.
Рассмотрим два произвольных (ненулевых) вектора 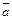 и
и  и отложим их от некоторой точки
и отложим их от некоторой точки  пространства.
пространства.
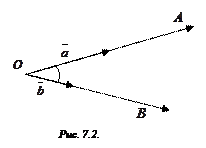 Точка
Точка  и вектор
и вектор 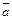 определяют луч
определяют луч 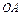 , точка
, точка 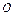 и вектор
и вектор  определяют луч
определяют луч 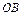 . Лучи
. Лучи 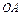 и
и 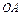 в свою очередь определяют два угла. Тот из них, который не больше развернутого, будем называть углом между векторами
в свою очередь определяют два угла. Тот из них, который не больше развернутого, будем называть углом между векторами 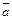 и
и  и обозначать
и обозначать 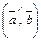 .
.
Очевидно, что угол между векторами не зависит от выбора точки 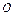 .
.
Определение. Углом между вектором 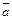 и осью
и осью 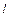 называют угол между вектором
называют угол между вектором 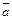 и ортом
и ортом  оси
оси 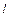 .
.
Теорема 7.3. Скалярная ортогональная проекция вектора 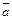 на ось
на ось 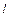 равна произведению модуля этого вектора на косинус угла между вектором и осью
равна произведению модуля этого вектора на косинус угла между вектором и осью 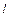 :
:
 . (7.8)
. (7.8)
Следствие. Равные векторы имеют равные проекции на одну и ту же ось
|
|
|
Дата добавления: 2014-01-07; Просмотров: 464; Нарушение авторских прав?; Мы поможем в написании вашей работы!