
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Кривые Гильберта
|
|
|
|
На рис. 3.2 приведен пример кривых Гильберта.

Рис. 3.2. Кривые Гильберта
Этот узор состоит из суперпозиции пяти кривых. Три наложенные друг на друга кривые имеют форму Н1, Н2 и Н3 (см. рис. 3.3.)

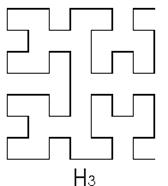
Рис. 3.3. Наложенные кривые
Нi+1 получается соединением четырех экземпляров Нi вдвое меньшего размера, повернутых соответствующим образом и "стянутых" вместе тремя прямыми линиями. Н1 можно считать состоящей из четырех вхождений пустой Н0, соединенных этими же тремя линиями. Кривая Нi называется кривой Гильберта i ‑го порядка в честь ее первооткрывателя Д.Гильберта.
Если каждая кривая Нi состоит из четырех вдвое меньших Нi-1, то процедура для рисования Нi будет включать четыре обращения для рисования Нi-1, соответствующим образом повернутых и уменьшенных вдвое. Обозначим эти четыре части через А, В, С и D.

Это кривые Гильберта 1-го порядка.
Соединительные прямые будем обозначать стрелками, указывающими соответствующее направление. Будем предполагать, что направление задается целым параметром i как i·45 градусов.
Тогда получаем:  при i = 0,
при i = 0,  при i = 2,
при i = 2,  при i = 4,
при i = 4,  при i =6.
при i =6.
Для построения A, B, С, D получается следующая схема рекурсий:
A: D  A
A  A
A  B
B
B: C 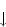 B
B 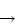 B
B  A
A
C: B 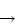 C
C 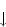 C
C  D
D
D: A  D
D  D
D 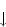 C
C
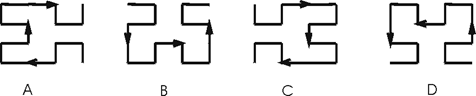
Кривые Гильберта 2-го порядка.
Для рисования линии будем использовать процедуру:
Line(i, s: integer), где i - направление, s - длина отрезка.
Используя эту процедуру, с помощью рекурсивных обращений напишем процедуру, соответствующую схеме А:
Procedure A(i, s: integer);BEGIN if i>0 then begin D(i-1,s); Line(4,s); A(i-1,s); Line(6,s); A(i-1,s); Line(0,s); B(i-1,s); end;END;Аналогично составляются процедуры для В, С, D. Процедура А инициируется главной программой по одному разу для каждой из кривых Гильберта. Главная программа определяет начальную точку кривой, т.е. исходные координаты (x0,y0) и начальное значение длины отрезка u (желательно, чтобы u=2n).
|
|
|
Эта программа рисует кривые Гильберта 5-го порядка.
Uses Crt, Graph; Var x:Real; GrD, GrM:integer; i,x0,y0,u:integer;procedure Line(i, s: integer);BEGIN x:=i*45/180*pi; setlinestyle(0,0,1); LineRel(Round(s*cos(x)),Round(s*sin(x)));END;Procedure B(i, s: integer);forward;Procedure C(i, s: integer);forward;Procedure D(i, s: integer);forward;Procedure A(i, s: integer);BEGIN if i>0 then begin D(i-1,s); Line(4,s); A(i-1,s); Line(6,s); A(i-1,s); Line(0,s); B(i-1,s); end;END;Procedure B;BEGIN if i>0 then begin C(i-1,s); Line(2,s); B(i-1,s); Line(0,s); B(i-1,s); Line(6,s); A(i-1,s); end;END;Procedure C;BEGIN if i>0 then begin B(i-1,s); Line(0,s); C(i-1,s); Line(2,s); C(i-1,s); Line(4,s); D(i-1,s); end;END;Procedure D;BEGIN if i>0 then begin A(i-1,s); Line(6,s); D(i-1,s); Line(4,s); D(i-1,s); Line(2,s); C(i-1,s); end;END;BEGIN {Кривые Гильберта Н1...Н5} Grd:= Detect; InitGraph(GrD,GrM, ' путь драйвера '); if GraphResult=GrOk then begin x0:=450; y0:=350; u:=128; i:=1; while i<=5 do begin MoveTo(x0,y0); A(i,u); i:=i+1; u:=u div 2; x0:=x0+(u div 2); y0:=y0+(u div 2); Readln; end; CloseGraph; end;END.|
|
|
|
Дата добавления: 2014-01-07; Просмотров: 689; Нарушение авторских прав?; Мы поможем в написании вашей работы!