III. Прямоугольные и геодезические общеземные системы координат

Система общеземных геоцентрических прямоугольных координат, фиксированная по отношению к Земле, определяется следующим образом:

- Начало в центре масс Земли.

- Ось Z проходит через УЗП.

- Ось Х проходит через точку G пересечения плоскости экватора и начального меридиана, определяемого как начальный меридиан для счёта долгот совокупности станций, реализующих координатную систему.

- Ось У находится в экваториальной плоскости и дополняет систему до правой.

Для обозначения этой системы могут встречаться такие названия как «общеземная система» или «средняя земная система». Последний термин указывает на использование некоторого среднего земного полюса, каковыми являются и УЗП, и МУН.

Земные геоцентрические системы реализуются в виде геодезических сетей, построенных методами космической геодезии (или с обязательным применением методов космической геодезии). Пункты таких сетей распределены по всему земному шару или по значительной его части. Чем более точны положения этих точек, тем меньше остаточные ошибки, и более точна реализация координатной системы.

В понятие земной геоцентрической системы входят не только координаты пунктов, которые закрепляют данную систему на местности, но и ряд других параметров, характеризующих её. В первую очередь это параметры земного эллипсоида, определяющие размеры и форму Земли. Для построения эллипсоида используют два главных параметра: экваториальный радиус а и сжатие α. Остальные параметры, определяющие размеры и форму эллипсоида можно вычислить по этим двум параметрам.

Из других параметров нужно указать параметры, представляющие гравитационное поле Земли, параметры связи с другими системами координат, число которых может достигать многих тысяч. Поэтому, когда говорят о современной геоцентрической системе координат (или системе отсчёта) подразумевается система геодезических параметров Земли.

Все геоцентрические системы связаны с определёнными эллипсоидами, названия которых обычно совпадают с названием самой системы. В этом случае возможно использование не только декартовых, но и эллипсоидальных (сфероидических) координат: геодезической широты В, геодезической долготы L и высоты над эллипсоидом Н. Для определения геодезических координат из точки А проводится нормаль к эллипсоиду АС. Геодезической широтой В называют угол между нормалью и плоскостью экватора эллипсоида, а геодезической долготой L – угол, отсчитываемый против часовой стрелки от начального меридиана до меридиана пункта. Прямоугольные координаты Х,У, Z вычисляются по геодезическим координатам В, L, Н по формулам:

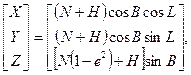
где 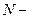радиус кривизны эллипсоида в первом вертикале, определяемый как

При переходе от прямоугольных координат к геодезическим определение долготы не вызывает затруднений:

а определение широты возможно несколькими способами. Их делят на итеративные и замкнутые. Из алгоритмов первой группы приведём метод, в котором геодезическая широта В находится по формуле:

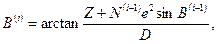
где 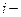номер итерации, повторяющейся до тех пор, пока 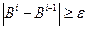(точность вычислений); проекция радиус-вектора на плоскость экватора:

а величина 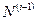находится из предыдущего приближения. Эллипсоидальная высота Н определяется по формуле:

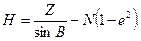
Дата добавления: 2014-01-07