С двумя переменными

Геометрический смысл линейного неравенства

Рассмотрим линейное неравенство с двумя переменными 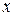и

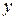
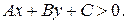(16)

Здесь 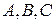– фиксированные вещественные числа, и 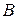не равны нулю одновременно. О геометрическом смысле этого неравенства можно говорить, если на плоскости 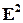выбрать аффинный репер 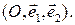Тогда неравенство (16) задает фигуру 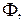состоящую из всех точек плоскости, координаты которых являются решениями неравенства. Отметим, что фигура не пуста. Чтобы в этом убедиться, возьмем любую точку 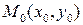на прямой и отложим от нее вектор 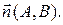Получим точку (рис. 9). Так как

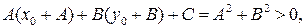
то Рассмотрим наряду с неравенством (16) соответствующее ему уравнение

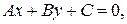(17)

которое в данном репере задает прямую, обозначим ее Пусть и – две точки, не лежащие на прямой Подставив их координаты в левую часть уравнения (17), получим два ненулевых числа 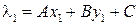и 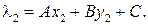Справедлива следующая лемма.

Лемма 2.3.1. Отрезок 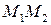пересекает прямую тогда и только тогда, когда числа и разных знаков.

Доказательство. Рассмотрим формулы из параметрических уравнений прямой, проходящей через точки и

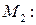
(18)

Очевидно, формулы (18) задают отрезок 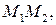если Следовательно, пересечение 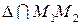задается системой уравнений:

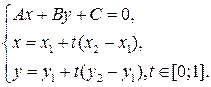
Подставим выражения 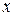и 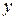в первое уравнение, получим уравнение с одним неизвестным

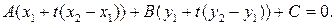
После раскрытия скобок это уравнение можно переписать в виде

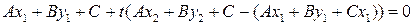
или

Несложный анализ показывает, что последнее уравнение имеет единственное решение 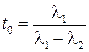такое, что 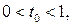тогда и только тогда, когда 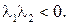Таким образом, отрезок 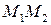пересекает прямую тогда и только тогда, когда числа и разных знаков. 

Утверждение 2.3.1. Линейное неравенство (16) в произвольном аффинном репере 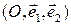задает одну из полуплоскостей, на которые прямая с уравнением (17) разбивает плоскость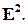

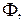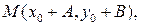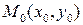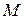Доказательство. Ранее мы отмечали, что фигура которая задается неравенством (16), не пуста, этой фигуре принадлежит, например, точка где – точка прямой Поскольку точка не лежит на прямой то 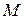лежит в одной из двух полуплоскостей, на которые плоскость 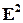разбивается прямой Обозначим эту полуплоскость , вторую полуплоскость 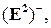и покажем, что 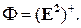Точка 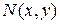лежит в полуплоскости тогда и только тогда, когда отрезок 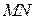не пересекает прямую В силу леммы 2.3.1 последнее условие эквивалентно тому, что числа и 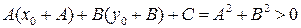одного знака, т.е. положительны (рис. 9). 

Рис. 9

Дата добавления: 2014-01-07