
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Дослідження опуклості графіка функції
|
|
|
|
Означення 12.2. Будемо говорити, що функція
1) строго опукла вниз на інтервалі  , і позначати
, і позначати 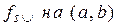 , якщо
, якщо 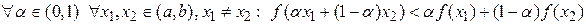 ;
;
2) не строго опукла вниз на інтервалі  , і позначати
, і позначати  , якщо
, якщо
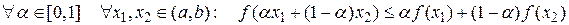 ;
;
3) строго опукла вгору на інтервалі  , і позначати
, і позначати  , якщо
, якщо
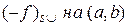 ;
;
4) не строго вгору на інтервалі  , і позначати
, і позначати 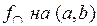 , якщо
, якщо
 ;
;
5) опукла на  , якщо функція
, якщо функція  задовольняє хоч одну з умов 1)-4).
задовольняє хоч одну з умов 1)-4).
 Зауваження 12.2. Геометрично умова, наприклад, строгої опуклості функції
Зауваження 12.2. Геометрично умова, наприклад, строгої опуклості функції  на інтервалі
на інтервалі  означає, що для будь-якої внутрішньої точки
означає, що для будь-якої внутрішньої точки 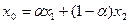 відрізка
відрізка  відповідна точка
відповідна точка 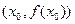 графіка функції
графіка функції  лежить нижче ніж точка
лежить нижче ніж точка 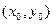 ,
,  , хорди, що зв’язує кінці
, хорди, що зв’язує кінці  і
і  графіка функції
графіка функції  .
.
Теорема 12.4. (Необхідні і достатні умови опуклості функції в термінах функції нахилу). Нехай 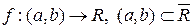 . Для довільної
. Для довільної 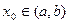 означимо функцію
означимо функцію 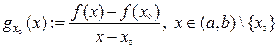 , яку будемо називати функцією нахилу функції
, яку будемо називати функцією нахилу функції  . Тоді: 1) функція
. Тоді: 1) функція  строго опукла вниз на інтервалі
строго опукла вниз на інтервалі 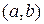 тоді і тільки тоді, коли для довільно вибраної точки
тоді і тільки тоді, коли для довільно вибраної точки 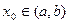 функція
функція  строго зростає на інтервалі
строго зростає на інтервалі 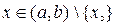 ; 2) функція
; 2) функція  не строго опукла вниз на інтервалі
не строго опукла вниз на інтервалі 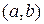 тоді і тільки тоді, коли для довільно вибраної точки
тоді і тільки тоді, коли для довільно вибраної точки 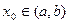 функція
функція  не спадає на інтервалі
не спадає на інтервалі 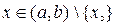 . Тобто,
. Тобто,
1)  ;
;
2)  .
.
Доведення. Доведемо тільки першу частину тереми. Розглянемо три можливі випадки розташування точок  на інтервалі
на інтервалі  .
.
а) Нехай 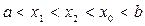 . Виберемо за
. Виберемо за 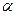 число
число 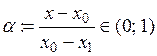 . Тоді
. Тоді 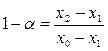 , тому,
, тому, 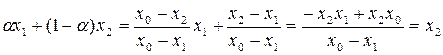 . Отже,
. Отже, 

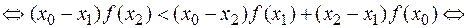

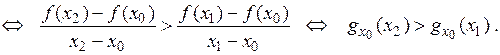
Звідки випливає, що функція  строго опукла вниз на інтервалі
строго опукла вниз на інтервалі 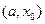 тоді і тільки тоді, коли функція
тоді і тільки тоді, коли функція  на ньому строго зростає.
на ньому строго зростає.
Аналогічно доводиться твердження і для наступних розташувань цих точок  та
та  . (Довести самостійно!!!)
. (Довести самостійно!!!)
Доведення другої частини теореми відрізняється від попередньої тільки заміною відповідних знаків строгої нерівності на знаки, нестрогої нерівності. (Довести самостійно!!!). Теорему доведено.
Теорема 12.5. (Необхідні і достатні умови опуклості функції, яка має похідну). Нехай функція  визначена і має скінчену похідну на деякому інтервалі
визначена і має скінчену похідну на деякому інтервалі 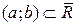 . Тоді: 1) функція
. Тоді: 1) функція  строго опукла вниз на інтервалі
строго опукла вниз на інтервалі 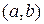 тоді і тільки тоді, коли і функція строго зростає на цьому інтервалі тоді і тільки тоді, коли перша похідна функції
тоді і тільки тоді, коли і функція строго зростає на цьому інтервалі тоді і тільки тоді, коли перша похідна функції  строго зростає на цьому інтервалі; 2) функція
строго зростає на цьому інтервалі; 2) функція  не строго опукла вниз на інтервалі
не строго опукла вниз на інтервалі 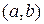 тоді і тільки тоді, коли перша похідна функції
тоді і тільки тоді, коли перша похідна функції  не спадає на цьому інтервалі. Тобто,
не спадає на цьому інтервалі. Тобто,
|
|
|

Доведення. Доведемо, наприклад, тільки твердження 2), так як інше доводиться аналогічно.
a) Необхідність. Нехай функція  не строго опукла вниз на інтервалі
не строго опукла вниз на інтервалі  . Покажемо, що тоді функція
. Покажемо, що тоді функція  не спадає на
не спадає на  , тобто для довільних точок
, тобто для довільних точок  з інтервалу
з інтервалу  таких, що
таких, що  , виконується нерівність
, виконується нерівність 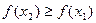 . Для цього виберемо довільні точки
. Для цього виберемо довільні точки  . Згідно твердження попередньої теореми з умови нестрогої опуклості вниз функції
. Згідно твердження попередньої теореми з умови нестрогої опуклості вниз функції  випливає справедливість нерівностей
випливає справедливість нерівностей 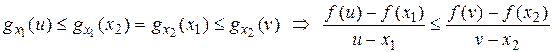 . Перейшовши до границі в лівій частині останньої нерівності при умові, що
. Перейшовши до границі в лівій частині останньої нерівності при умові, що  , а в правій частині при умові, що
, а в правій частині при умові, що  отримаємо, що
отримаємо, що 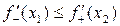 . Але за умовою існування скінченої похідної функції
. Але за умовою існування скінченої похідної функції  в усіх точках інтервалу
в усіх точках інтервалу 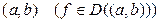 випливає, що
випливає, що 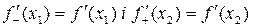 . Тому,
. Тому,  , тобто, похідна
, тобто, похідна 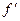 не спадає на
не спадає на  .
.
b) Достатність. Нехай похідна 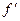 не спадає на
не спадає на  . Зафіксуємо довільну точку
. Зафіксуємо довільну точку 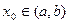 і обчислимо похідну функції нахилу
і обчислимо похідну функції нахилу 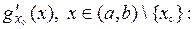
 .
.
Застосувавши теорему Лагранжа до другого доданка чисельника, отримаємо:

Дійсно, якщо 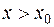 , то
, то 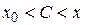 , тому,
, тому,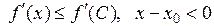 . Отже,
. Отже,  . Крім того, за умови існування скінченої похідної
. Крім того, за умови існування скінченої похідної 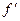 в довільній точці
в довільній точці  випливає, що існують і співпадають скінчені границі
випливає, що існують і співпадають скінчені границі 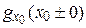 , а саме:
, а саме: 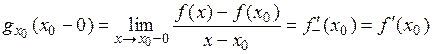 ,
,
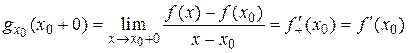 .
.
Тому, якщо доозначити функцію нахилу  , в точці
, в точці 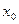 , як
, як  , то функція
, то функція  стане неперервною в цій точці. А значить, згідно твердження теореми 12.3., функція
стане неперервною в цій точці. А значить, згідно твердження теореми 12.3., функція  не спадає на всьому інтервалі
не спадає на всьому інтервалі  , звідки за теоремою 12.4, випливає, що функція
, звідки за теоремою 12.4, випливає, що функція  не строго опукла вниз на
не строго опукла вниз на  , що і потрібно було довести.
, що і потрібно було довести.
Завдання для самостійної роботи12.1. Довести перше твердження теореми 12.5.
Теорема 12.6. (Необхідні і достатні умови опуклості функції в термінах її другої похідної). Нехай в усіх точках інтервалу  функція
функція  має другу скінчену похідну
має другу скінчену похідну  . Тоді:
. Тоді:
|
|
|
1) функція  не строго опукла вниз на
не строго опукла вниз на  тоді і тільки тоді, коли друга похідна функції
тоді і тільки тоді, коли друга похідна функції  є невід’ємною на
є невід’ємною на  .
.
2) функція  строго опукла вниз на
строго опукла вниз на  тоді і тільки тоді, коли друга її похідна невід’ємна на
тоді і тільки тоді, коли друга її похідна невід’ємна на  , і при цьому не існує жодного інтервалу
, і при цьому не існує жодного інтервалу 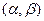 , що лежить всередині
, що лежить всередині  , на якому друга похідна
, на якому друга похідна  тотожньо дорівнює нулю.
тотожньо дорівнює нулю.
Доведення. Твердження випливає з доведених теорем 12.5, 12.1, 12.2.
Зауваження 12.3. За означенням 12.2. легко бачити, що твердження теорем 12.4-12.6 залишаються в силі, якщо в цих теоремах замінити умову строгої або нестрогої опуклості вниз функції  на умову відповідної опуклості вгору, умову зростання функції нахилу або похідної
на умову відповідної опуклості вгору, умову зростання функції нахилу або похідної 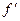 на умову її спадання, умову додатності або невід’ємності другої похідної
на умову її спадання, умову додатності або невід’ємності другої похідної  на умову її від’ємності або недодатності відповідно.
на умову її від’ємності або недодатності відповідно.
|
|
|
|
Дата добавления: 2014-01-07; Просмотров: 1105; Нарушение авторских прав?; Мы поможем в написании вашей работы!