Математические модели для оценки надежности ЛК в процессе отработки и испытаний

Исходя из анализа устройства и функционирования ЛК как сложной системы и как объекта надежности для оценки ПН его в процессе отработки рассматривают следующие модели:

· Биномиальная классическая модель

· Биномиальная рекуррентная модель

· Биномиальная модель, дифференцированная по типам (причинам) отказов

· Аппроксимационная модель

Биномиальная классическая модель

В модели, относящейся к схеме испытаний Я. Бернулли (биномиальной модели), рассматривает­ся последовательность n независимых испытаний, в каждом из ко­торых возможны два исхода: А и (например, успех и отказ). Вероятности исходов равны р и q соответственно, причем р = 1 – q. В каждом испытании вероятность р постоянна. При этих предпосылках рассматривается случайная величина – возможное число исходов вида (например, отказов) в n испытаниях. Вероят­ность 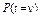того, что в n испытаниях будет ровно отказов, и вероятность 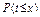того, что в n испытаниях число отказов не превысит некоторого фиксируемого значения х, выражают с по­мощью соотношений

, ,

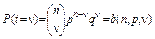где 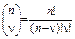; 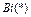и 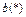– обозначения, используемые далее для сокращения записи; n и р – параметры, а выражение 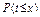– функция биномиального распределения. Корн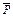и и уравнений (Клоппера-Пирсона), , 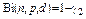являются соответственно верхней и нижней границами доверительного интервала [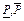] для параметра p, причем .

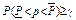В приведенных уравнениях величина d – число наблюдаемых (зарегистрированных) исходов (отказов) в n испытаниях; – доверительная вероятность.

Кор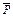ни и выражают в виде соотношений 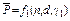, вычисляют через неполную бета-функцию (betainv).

Биномиальная рекуррентная модель

Рекуррентная модель "дифференцированная по календарю доработок" учитывает неоднородность исходных ста­тистических данных, текущей и априорной информации об отрабатывае­мой конструкции (неоднородность, обусловленную воздействиями на испытываемое изделие в процессе его отработки в виде доработок, варьированием «конфигурацией» объекта испытаний, разнообразием ре­жимов и условий испытаний), основывается на использовании идеи формулы полной вероятности. При этом вероятность осуществления события А, состоящего в безотказном функционировании изделия после проведения доработки (изменения режима испытаний):

,

где 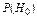– вероятность осуществления гипотезы, заключающейся в том, что доработка (изменение режима испытаний) не изменила надёжности изделия и результаты испытаний до и после доработки принадлежат одной генеральной совокупности. Оценки вероятности 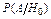и вероятности определяются как

,

где m₁ и m₂ – число отказов в испытаниях до и после доработки соответственно; n₁ и n₂ – число испытаний до и после доработки соответственно. Тогда оценка вероятности Р(А)

,

где – оценка вероятности осуществления гипотезы Н ₀; – оценка вероятности осуществления гипотезы, альтернативной Н ₀; 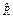– весовой коэффициент, имеющий смысл вероятности осуществления гипотезы Н ₀ об однородности статистических данных. При ; при 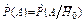; в реальных условиях отработки .

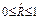Используют различные подходы к расчёту оценки 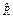весового коэффициента. В лекции предложена следующая модель такого расчёта:

,

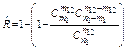где m ₁ и n ₁ – число отказов и число испытаний до доработки; m ₂ и n ₂ – число отказов и число испытаний в серии после оцениваемой доработки до следующей; m ₁₂ = m ₁ + m ₂ и n ₁₂ = n ₁ + n ₂.

При представлении исходных данных в виде, , 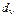, являющихся количеством испытаний и отказов после (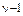) доработки и до n-й доработки (,– исходы испытаний до первой доработки, ,– исходы испытаний после последней m -й доработки) определяют оценку вероятности ненаступления отказов 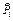для данного этапа отработки (после m доработок) в соответствии с многошаговой процедурой.

На первом шаге учитывают эффективность только первой доработки. При этом используют данные:– количество испытаний и число отказов i -го типа до проведения первой доработки; – количество испытаний и число отказов i -го типа в период от первой до второй доработки. По ним определяют весовой показатель (вероятность того, что первая доработка (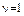) не изменила надежности блока):

,

где , , .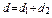

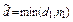Оценка вероятности ненаступления отказа данного типа после проведения первой доработки .

Эквивалентный объем испытаний (до второй доработки или общий, если последней доработки не было) , эквивалентное число отказов .

На втором шаге вычислений учитывают эффект второй доработки. При этом в качестве исходных данных аналогично принимают: 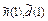– эквивалентные исходы испытаний до второй доработки; 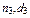– количество испытаний и число отказов i -го типа от второй до третьей доработки. По этим данным определяют весовой показатель W(2) (вероятность того, что вторая доработка не изменила надежности блока).

Оценка вероятности ненаступления отказа данного типа после проведения второй доработки по результатам испытаний до третьей доработки

.

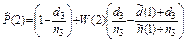Эквивалентный объем испытаний (до третьей доработки или общий) 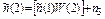, эквивалентное число отказов .

Аналогично вычисляют оценки P (n) с учетом эффективности всех последующих доработок, .

Конечная оценка вероятности ненаступления отказов (после проведения всех доработок) .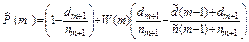

Эквивалентный объем испытаний , эквивалентное число отказов .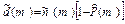

Нижняя доверительная граница уровня 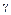или .

Биномиальная модель, дифференцированная по типам (причинам) отказов

Модель "дифференцированная по причинам отказов". Точечная оценка вероятности безотказной работы при наличии отказов определяется по формуле 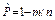, где n – число импульсов за период испытаний; m – число отказов при n импульсах.

Точечная оценка вероятности безотказной работы при отсутствии отказов определяется по формуле .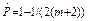

Вероятности безотказной работы изделия при проведении доработок по устранению причин конструкционных отказов:

· , где – оценка ВБР по общему числу импульсов и отказов, для устранения причин которых доработки не производились; k – число типов отказов, по которым проводятся доработки;

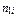· ; ; , – число отказов i -го типа и импульсов до проведения по ним доработок; – число импульсов без отказов после проведения доработки по устранению причин возникновения i -го типа отказа, включая результаты специальных испытаний отказавшего узла (механизма, детали) для подтверждения эффективности проведенной доработки; 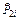– оценка ВБР после проведения доработки с изменением КД по устранению конструкционного отказа.

При использовании модели "дифференцированной по отказам" НДГ ВБР изделия Р определяют в следующей последовательности:

· тип отказов с минимальным суммарным настрелом ;

· эквивалентное число отказов mэ = N(1–);

· значение НДГ ВБР Р ЛК при заданном значении доверительной вероятности γ Р = betainv (1–γ, N–mэ,+1). Здесь betainv – неполная бета-функция.

Аппроксимационная модель

Аппроксимационная модель характеризуется следующими допущениями: испытания в процессе отработки изделия делятся на этапы моментами внесения доработок; внутри этапа испытания (опыты) независимые; надёжность объекта испытаний изменяется только в результате доработок; доработка может проводиться как после отказа, так и после успешного испытания; относительный вклад каждой доработки в изменение надёжности изделия выражается числом устранённых причин отказов; вклад устранения одной причины отказа в изменение надёж­ности отрабатываемого изделия постоянный для данного периода испыта­ний.

Модель строят на основе логико-вероятностного принципа. При этом в виде линейной аппроксимации анализируют приращения значений оцениваемого ПН (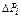 – приращение вероятности безотказной работы) в результате проведения доработок конструкции:

,

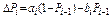где а_i – коэффициент, характеризующий изменение оставшейся после (i– 1)-й доработки вероятности отказа (1 –Р_{i- 1}) за счёт i -й доработки; b_i – коэффициент, характеризу­ющий снижение достигнутой вероятности безотказной работы Р_{i- 1} за счёт i -й доработки; i – индекс, характеризующий номер доработки (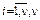 – количество доработок). Известна связь i = i (j), где j – номер опыта в последовательности испытаний ( – объём испытаний). Линейная модель учитывает возможность как повышения, так и снижения достигнутого значения Р_{i- 1}, т.е. 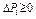. Коэффициент a_i характеризует эффективность проведенной доработки изделия, т.е. долю вероятности отказа, преобразуемую в приращение 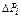; коэффициент b_i – негативную сторону доработки и количественно определяет степень уменьшения достигнутой Р_{i- 1}. Значение коэффициента а_i зависит от объёма получаемой при испытаниях информации, позволяющей достоверно устанавливать и устранять причины отказов, значение коэффициента b_i – информации, анализ которой привел к ошибочным выводам относительно причин отказов и соответственно к доработкам, снижающим ПН. Естественно, что чем больше причин отказов устраняется одной доработкой, тем существеннее её влияние на ПН изделия. Поэтому вводится предположение, что а_i = k_ia; b_i = k_ib, где k_i – количество устраняемых i -й доработкой причин отказов; а, b – постоянные коэффициенты, характеризующие эффективность устранения одной причины отказа. Таким образом, функция изменения ПН отрабатываемого изделия имеет вид , где Р ₀ – значение ПН изделия до первой доработки. После преобразований, проведенных по рассмотренной схеме, выражение для модели роста ПН отрабатываемого изделия приобретает вид

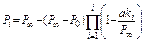, где .

Для решения задачи статистического оценивания параметров модели а, Р₀ и по результатам отработки изделия может быть использован метод максимального правдоподобия, применение которого пред­полагает справедливость допущения о независимости результатов испы­таний. Исследование статистической независимости результатов ис­пытаний, относящихся к разным этапам (после i -й и ()-й доработок), сводится к определению и исследованию корреляционного момента дискретной случайной величины X (отражающей исход j -го испытания после i -й доработки) и Y ((j+k)-го испытания после ()-й доработки): 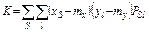, где m_x, m_y – мате­матические ожидания случайных величин X и Y. После преобразования

,

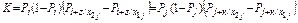где P_i = P_j – вероятность успеха в j -м испытании; 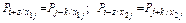– условные вероятности успеха в (j+к)-м испытании после (i+z)-й доработки, если в j -м испытании был отказ х_1j или успех х_2j. Коэффициент корреляции величин X и Y равен

.

В соответствии с принятыми допущениями изменение вероятности от P_j до Р_j+k происходит только из-за внесения доработок, которые возможны после успешных испытаний или отказов. Факты внесения доработок не связаны с исходами испытаний и являются достоверными событиями. Это предопределяет статистическую независимость исходов испытаний, т.е. вероятност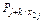и и безусловные и равны между собой и . В силу показанной независимости результатов испытаний вероятность получения 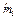отказов в n_i испытаниях определяется биномиальным выражением . Вероятность получения всей выборки (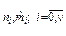), т.е.функция правдоподобия, равна произведению вероятностей:

.

При этом

В качестве оценок максимального правдоподобия принимают значения , при которых функция правдоподобия при заданной выборке () обращается в максимум (–ln L в минимум). Получаемые оценки максимального правдоподобия состоятельные, асимптотически несмещенные и асимптотически эффективные (для больших выборок). Предельным законом распределения оценок максимального правдоподобия является трёхмерный нормальный закон распреде­ления со средним значением () и матрицей ковариаций:

û

.

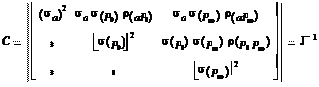Здесь J – информационная матрица Фишера, элемент которой

.

Точность оценок параметров можно определить, если в
выражении для С или J вмеcто истинных значений параметров а,
Р ₀, подставить оценки максимального правдоподобия . Дисперсия оценки Р_i может быть найдена заменой не­линейной зависимости для Р_i, линеаризованной:

.

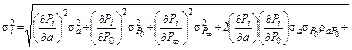
При нормальном законе распределения оценки 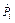доверительный интервал для оценки 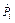в каждом сечении процесса (считая со средним квадратическим отклонением ):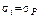

· двусторонний доверительный с коэффициентом доверия ;

· односторонний нижний доверительный предел 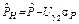, где 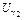– квантиль нормального распределения.

В практических задачах при анализе точности исследования надёжности отрабатываемых изделий рекомендуется для упрощения расчётов оценивать сверху среднее квадратическое отклонение оценки ПН на последнем этапе (после последней доработки) по формуле: .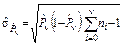

Рассмотренная модель роста надёжности отрабатываемого изделия при дополнительных упрощающих допущениях (в каждой доработке устраняется одинаковое количество причин отказов k_i=k= const и при проведении n испытаний доработок проводятся равномерно, т.е. существует линейная зависимость между номером доработки i и номером испытаний j ()) сводится к модели математического ожидания: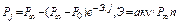, описывающей изменение надёжности отрабатываемого изделия в зависимости от номера испытаний j.

Основная сфера применения упрощенных моделей роста надёжности – задачи прогнозирования. При этом, считая частоту доработок 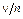аналогом вероятности проведения доработки, становится возможным определение величины этой характеристики при прогнозировании процесса изменения надёжности отрабатываемой конструкции по данным отработки подобных образцов в близких условиях.

Дата добавления: 2014-01-07