Напряженное состояние в точке

ЛЕКЦИЯ №5

Условие, при котором две прямые лежат в одной плоскости.

Пересечение прямой и плоскости

Пусть дана плоскость и прямая: или параметрическое задание:. Координаты точки пересечения прямой и плоскостью можно получить, совместно решая имеющуюся систему 3 уравнений с 3 неизвестными. Но эффективнее это сделать с использованием уравнений в параметрической форме, т.е. находим параметр t из уравнения: находим значение параметра t:

и далее из параметрического урав-нения находим координаты соответствующей точки.

Пусть даны две прямые в пространстве:, и пусть они проходят через точки: и. Тогда уравнения этих прямых имеют следующий вид: и.

Причём:. Тогда имеем: Три вектора: принадлежат одной плоскости, а тогда:, т.е.

Пример 4: Составить уравнение прямой, проходящей через точку, пересекающую прямую и перпендикулярно к прямой:. Уравнение искомой прямой будет:

, где координаты направляющего вектора определяются из условий:;

. Т.о. получили два уравнения: Поделив оба уравнения, например на, и решая эту систему уравнений относительно отношений, получим: или. Тогда принимая: будем иметь искомое уравнение:.#

Для того чтобы оценить прочность детали нужно знать напряжение в любой точке этой детали и в любом направлении. Совокупность нормальных и касательных напряжений по всем площадкам. Проходящим через данную точку тела называется напряженным состоянием в точке.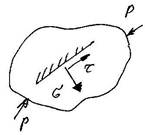

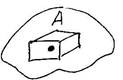
Для исследования напряженного состояния в точке в её окрестности выделяется элементарный параллелепипед бесконечно малых размеров. Напряжённое состояние этого параллелепипеда соответствует напряженному состоянию в точке.

Дата добавления: 2014-01-07