Случайные переменные

Случайные сигналы

Основной задачей системы связи является передача информации по каналу связи. Все полезные сигналы сообщений появляются случайным образом, т.е. приемник не знает заранее, какой из возможных символов сообщений будет передан. Кроме того, вслед­ствие различных электрических процессов возникают шумы, которые сопровождают информационные сигналы. Следовательно, нам нужен эффективный способ описания случайных сигналов.

Пусть случайная переменная Х(А) представляет функциональное отношение между случайным событием А и действительным числом. Для удобства записи обозначим случайную переменную через X, а ее функциональную зависимость от А будем считать явной. Случайная переменная может быть дискретной или непрерывной. Функция распределения F_x(х) случайной переменной X описывается выражением

F_x(x)=P(X≤ x), (1.4)

где Р(Х ≤ х) — вероятность того, что значение, принимаемое случайной переменной X, меньше действительного числа х или равно ему. Функция распределения F_x(x) имеет следующие свойства:

1.0 ≤ F_x(x) ≤ 1

2. F_x(x₁) ≤ F_x(x₂), если x₁ ≤ x₂

3. F_x( −∞ ) = 0

4. F_x( +∞ ) = 1

Еще одной полезной функцией, связанной со случайной переменной X, является плотность вероятности, которая записывается следующим образом:

. (1.5,а)

Как и в случае функции распределения, плотность вероятности — это функция действительного числа х. Название "функция плотности" появилось вследствие того, что вероятность события x ₁ ≤ X ≤ x ₂ равна следующему:

P (x ₁ ≤ X ≤ x ₂) = P (X ≤ x ₂) – P (X ≤ x ₁) = (1.5,б)

= F_x(x ₂ ) – F_x(x ₁ ) =

.

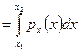Используя уравнение (4.5,6), можно приближенно записать вероятность того, что случайная переменная X имеет значение, принадлежащее очень узкому промежутку между х и х + Δ x:

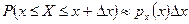. (1.5,в)

Таким образом, в пределе при Δ x, стремящемся к нулю, мы можем записать следующее:

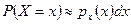. (1.5,г)

Плотность вероятности имеет следующие свойства:

1. p_x(х) ≥ 0

2.

Таким образом, плотность вероятности всегда неотрицательна и имеет единичную площадь. В тексте книги мы будем использовать запись р_х(х) для обозначения плотно­сти вероятности непрерывной случайной переменной. Для удобства записи мы часто будем опускать индекс X и писать просто р(х). Если случайная переменная X может принимать только дискретные значения, для обозначения плотности вероятности мы будем использовать запись р(Х=х_i).

Дата добавления: 2014-01-07