Алгебраические критерии устойчивости

Наиболее наглядными с этой точки зрения являются алгебраические критерии, предложенные Раусом (1875 г.) и Гурвицем (1895 г.). Так как эти критерии отличаются только деталями, ограничимся изложением критерия Гурвица. Гурвиц, формулируя свой критерий, ставил перед собой чисто математическую задачу: найти сравнительно простой метод, позволяющий определить, не имеет ли один из корней алгебраического уравнения положительную (или равную нулю) действительную часть. Как известно, если в качестве такого уравнения взять характеристическое уравнение системы, то ответ на этот вопрос позволит определить, устойчива ли данная система.

Для применения критерия Гурвица строится специальный определитель из коэффициентов характеристического уравнения. Для уравнения шестого порядка, например, определитель Гурвица имеет вид

a5	a6
a3	a4	a5	a6
a1	a2	a3	a4	a5	a6
	a0	a1	a2	a3	a4
			a0	a1	a2
					a0

Метод построения определителя состоит в том, что в правом нижнем углу записывается коэффициент a₀, а дальше по большой диагонали снизу — вверх — все коэффициенты по порядку: a₁, a₂, a₃,… a₅,.Основываясь на полученной таким образом большой диагонали, можно заполнить все остальные участки определителя; при этом справа от большой диагонали записываются по порядку коэффициенты с возрастающими номерами, слева — с убывающими. Если какой-либо из коэффициентов отсутствует, то на его место ставится 0. Например, слева от a₀ и справа от a_n всегда будут нули (n — порядок характеристического уравнения). Определитель может быть построен и другим методом; в левом верхнем углу записывается коэффициент a_n-1 , а справа от него по верхней строке определителя — все остальные коэффициенты с возрастающими номерами: a_n, 0,..., 0. Вторая строка начинается с a_n-3, и справа опять записываются коэффициенты с возрастающими номерами: a_n-2, a_n-1, a_n, 0,…,0. Все следующие строки определителя начинаются с последующих коэффициентов с нечетными номерами: a_n-5, a_n-7,…, справа от которых идут коэффициенты с возрастающими номерами. Так же как и в первом методе составления определителя, все отсутствующие коэффициенты заменяются нулями. Так как оба метода составления определителя дают одинаковый результат, можно, составляя определитель Гурвица с помощью одного из них, применить другой для проверки.

Анализируемое уравнение не будет иметь корней с положительной действительной частью, т. е. система, которой это уравнение соответствует, будет устойчива, если коэффициент a_n >0 и в определителе Гурвица миноры Δ₁, Δ₂, … Δ_n будут положительными. Если в исходном характеристическом уравнении коэффициент a_n <0, то, умножив все уравнение на -1, можно обеспечить выполнение условия a_n >0.

Миноры Гурвица являются частями определителя, например:

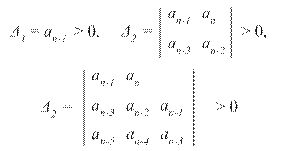
и т. д. Очевидно, что для уравнения n -го порядка Δ_n = a₀ Δ_n-1 (так как все остальные члены в нижней строке равны 0).

Следовательно, для проверки устойчивости системы достаточно найти миноры от Δ₁ до Δ_n-1.

Если один из миноров меньше нуля, то по меньшей мере один из корней будет иметь положительную действительную часть, а значит, система, которой соответствует это характеристическое уравнение, будет неустойчивой.

Так как при анализе устойчивости необходимо не только ответить на вопрос о том, устойчива ли система, но и определить, в каких пределах могут изменяться отдельные параметры элементов системы и как они влияют на устойчивость, то очевидно, что критерий Гурвица не позволяет получить полный ответ на этот вопрос. Действительно, изменение любого параметра системы приводит к новому характеристическому уравнению, а следовательно, нужно заново применять критерий Гурвица. Исключение составляют только самые простые системы, которые имеют характеристические уравнения второго и третьего порядков. Так как такие простые случаи сравнительно редко встречаются на практике, то и критерий Гурвица в последние годы применяется все реже.

Таким образом, применение критерия Гурвица к реальным системам приводит к сложным вычислениям, а главное, не позволяет выявлять влияние отдельных параметров элементов на работу системы в целом. Если, например, в результате анализа выяснилось, что система неустойчива, то критерий Гурвица не дает указаний, какой из параметров элементов системы и на какую величину должен быть изменен, чтобы сделать систему устойчивой. В более сложных случаях, когда необходимо обеспечить определенные параметры переходного процесса, критерий Гурвица не дает никаких сведений о влиянии параметров элементов системы на вид переходного процесса. Все эти недостатки, свойственные алгебраическим критериям (Рауса и Гурвица), естественно, ограничивают их применение.

Дата добавления: 2014-01-07