Плотность энергии электростатического поля

Энергия электростатического поля.

1. Энергия системы неподвижных точечных зарядов. Электростатические силы взаимодействия консервативны; следовательно, система зарядов обладает потенциальной энергией. Найдем потенциальную энергию системы двух неподвижных точечных зарядов и , находящихся на расстоянии r друг от друга. Каждый из этих зарядов в поле другого обладает потенциальной энергией:

, ,

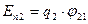где 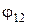и 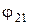- соответственно потенциалы, создаваемые зарядом в точке нахождения заряда и зарядом в точке нахождения заряда . При этом,

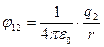и ,

Поэтому и .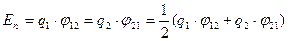

Добавляя к системе из двух зарядов последовательно заряды 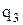, , 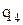…, можно убедиться в том, что в случае n неподвижных зарядов энергия взаимодействия системы точечных зарядов равна

, (8.12.1.)

где 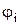- потенциал, создаваемый в той точке, где находится заряд 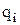, всеми зарядами, кроме i-го.

2. Энергия заряженного уединенного проводника. Пусть имеется уединенный проводник, заряд, емкость и потенциал которого соответственно равны q, C, 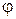. Увеличим заряд этого проводника на dq. Для этого необходимо перенести заряд dq из бесконечности на уединенный проводник, затратив на это работу, равную .

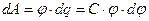Чтобы зарядить тело от нулевого потенциала до 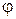, необходимо совершить работу

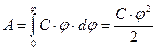. (8.12.2.)

Энергия заряженного проводника равна той работе, которую необходимо совершить, чтобы зарядить этот проводник:

. (8.12.3.)

Формулу (8.12.3.) можно получить и из того, что потенциал проводника во всех его точках одинаков, так как поверхность проводника является эквипотенциальной. Полагая потенциал проводника равным 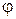, из (8.12.1.) найдем

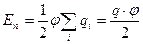, где - заряд проводника.

3. Энергия заряженного конденсатора. Как всякий заряженный проводник, конденсатор обладает энергией, которая в соответствии с формулой (8.12.3.) равна

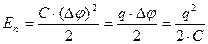, (8.12.4.)

где q - заряд конденсатора, C - его емкость, 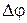- разность потенциалов между обкладками.

4. Энергия электростатического поля. Преобразуем формулу (8.12.4.), выражающую энергию плоского конденсатора посредством зарядов и потенциалов, воспользовавшись выражением для емкости плоского конденсатора 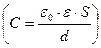и разности потенциалов между его обкладками (). Тогда получим

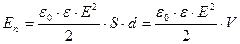, (8.12.5.)

где V=Sd - объем конденсатора. Формула (8.12.5.) показывает, что энергия конденсатора выражается через величину, характеризующую электростатическое поле, - напряженность Е.

Формулы (8.12.4.) и (8.12.5.) соответственно связывают энергию конденсатора с зарядом на его обкладках и с напряженностью поля. Возникает, естественно, вопрос о локализации электростатической энергии и что является ее носителем - заряды или поле? Ответ на этот вопрос может дать только опыт. Электростатика изучает постоянные во времени поля неподвижных зарядов, т.е. в ней поля и обусловившие их заряды неотделимы друг от друга. Поэтому электростатика ответить на поставленные вопросы не может. Дальнейшее развитие теории и эксперимента показало, что переменные во времени электрические и магнитные поля могут существовать обособленно, независимо от возбудивших их зарядов, и распространяются в пространстве в виде электромагнитных волн, способных переносить энергию. Это убедительно подтверждает основное положение теории близкодействия о локализации энергии в поле и что носителем энергии является поле.

Объемная плотность энергии электростатического поля (энергия единицы объема)

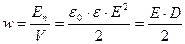. (8.12.6.)

Выражение (8.12.6.) справедливо только для изотропного диэлектрика, для которого выполняется соотношение: .

Дата добавления: 2014-01-07