
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Решение. Воспользуемся правилом произведения, число команд равно произведениючисел 18, 20и22, т.е. равно 7920
|
|
|
|
Задача 10. На плоскости задано множество A, состоящее из 8 точек. Три из них выкрашены в красный цвет и лежат на одной прямой, а остальные расположены так, что проходящая через пару точек прямая не содержит других точек множества. Через каждые две точки множества A проведено по прямой линии. Сколько всего прямых линий получилось?
Решение. Мы можем составить  пар точек и провести через них прямые, но не все они будут различны. Из трех красных точек мы можем составить
пар точек и провести через них прямые, но не все они будут различны. Из трех красных точек мы можем составить 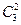 пар точек, и все они определяют одну и ту же прямую. Поскольку все остальные пары точек образуют разные прямые, надо вычесть из общего числа пар все пары, образованные тремя красными точками, и компенсировать это вычитание добавкой единицы, т.к. одну прямую эти точки все - таки образуют. Ответ:
пар точек, и все они определяют одну и ту же прямую. Поскольку все остальные пары точек образуют разные прямые, надо вычесть из общего числа пар все пары, образованные тремя красными точками, и компенсировать это вычитание добавкой единицы, т.к. одну прямую эти точки все - таки образуют. Ответ: .
.
Задача 11. Сколькими способами можно упорядочить множество 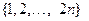 так чтобы каждое четное число имело четный номер?
так чтобы каждое четное число имело четный номер?
Решение. Множество номеров чисел в перестановке можно разбить следующим образом.  . Нам надо, чтобы первая группа этих номеров соответствовала нечетным числам, а вторая – четным. Таким образом, при каждой фиксированной перестановке нечетных чисел в первой группе номеров, имеется
. Нам надо, чтобы первая группа этих номеров соответствовала нечетным числам, а вторая – четным. Таким образом, при каждой фиксированной перестановке нечетных чисел в первой группе номеров, имеется 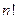 перестановок четных чисел во второй группе номеров. Таким образом, общее число перестановок равно
перестановок четных чисел во второй группе номеров. Таким образом, общее число перестановок равно 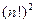 .
.
Задача 12. В ящике находится 20 деталей. Известно, что 5 из них являются стандартными. Из этих деталей выбирают 3. Сколько существует способов выбора трех деталей таких, чтобы среди них была, по крайней мере, одна стандартная?
Решение 1. Множество всех возможных выборов трех деталей из 20 содержит 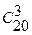 элементов, среди них
элементов, среди них 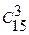 троек содержит тольконестандартные детали. Поэтому ответом задачи будет
троек содержит тольконестандартные детали. Поэтому ответом задачи будет 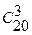 -
- 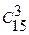 = 685.
= 685.
|
|
|
Решение 2. Указанное в условии множество троек можно представить как объединение трех (не пересекающихся!) множеств. Первое состоит из троек стандартных деталей. Их число 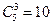 . Второе из троек, в которых две детали стандартные, а одна нестандартная, таких троек
. Второе из троек, в которых две детали стандартные, а одна нестандартная, таких троек 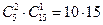 . Третье множество состоит из троек, содержащих ровно одну стандартную деталь. Таких троек -
. Третье множество состоит из троек, содержащих ровно одну стандартную деталь. Таких троек -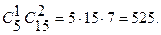
Поскольку эти множества не пересекаются, то чтобы получить ответ надо просуммировать полученные числа и убедится, что ответы совпали.
Комментарий. Простая идея разбить множество на непересекающиеся части, в каждой из которых подсчитать число элементов легче, широко используется при решении комбинаторных задач. Разбор этой задачи показывает, что решение можно получать разными способами. Конечно, каждый раз следует выбирать наиболее рациональный способ.
Задача 13. Из 7 разноцветных карточек разрезной азбуки составлено слово колокол. Ребенок, не умеющий читать, случайно рассыпал эти карточки. Сколькими способами из этих карточек он сможет снова составить слово колокол?
Решение. На карточках имеется 3 буквы о, 2 буквы к, 2 буквы л. Поэтому, первая буква слова колокол может быть выбрана 2 способами, вторая – 3 способами, третья – 2 способами. При уже выбранных первых трех буквах четвертая буква может быть выбрана еще 2 способами (поскольку одна буква о уже выбрана). Остальные буквы могут быть выбраны только одним способом. Таким образом, ответ равен произведению чисел 3, 2, 2, 2 т.е. равен 24.
Задача 14. Имеется прямоугольник, разбитый на клетки. По горизонтали n клеток, а по вертикали– m клеток. Можно двигаться только по сторонам клеток либо вправо, либо вверх. Сколько существует различных путей из левого нижнего угла в правый верхний угол?
Решение. Сопоставим ходам вдоль клеток цифры 0 и 1, таким образом, чтобы 0 означал движение вправо, а 1 – движение вверх. Тогда каждому пути соответствует набор из (n+m ) цифр, причем в каждом наборе будет ровно n нулей и m единиц. Сколько таких наборов? Всего в таком наборе имеется (n+m) позиций, и надо среди них разместить m единиц (на остальных местах нули). Выбор таких путей можно осуществить 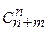 способами.
способами.
|
|
|
Задача 15. Сократите дробь: а)  ; б)
; б)  ; в)
; в)  ; г)
; г) 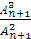 ; д)
; д)  ; е)
; е)  ; ж)
; ж)  .
.
Задача 16. Выполнить действия: а)  ; б)
; б) 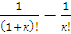 .
.
Задача 17. Решите уравнения: а)  ; б)
; б) ; в)
; в) 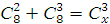 ; г)
; г) 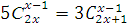 ; д)
; д)  .
.
|
|
|
|
Дата добавления: 2014-01-07; Просмотров: 787; Нарушение авторских прав?; Мы поможем в написании вашей работы!