
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Метод сопряженных направлений
|
|
|
|
Все описанные до сих пор прямые методы min-ии требуют бесконечного числа итераций для точного определения точки min0ма целевой функции. Это относится и к сильно выпуклым квадратичным функциям.
Однако существуют прямые итерационные методы, приводящие к точки min-ма сильно выпуклой квадратичной функции за конечное число шагов.
От таких методов разумно ожидать высокой эффективности и в случае выпуклой неквадратичной целевой функции. Опишем один из них.
Рассмотрим сначала проблему поиска точки min-ма сильно выпуклой квадратичной функции двух переменных. Ее линиями уровня являются эллипсы.
Пусть p и p
и p - направления главных осей эллипсов. Если из произвольной точки х
- направления главных осей эллипсов. Если из произвольной точки х ЄЕ
ЄЕ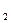 выполнить итерационную процедуру х
выполнить итерационную процедуру х =х
=х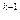 +
+ p
p , k=1,2, где величина шага
, k=1,2, где величина шага  - находится из условия исчерпывающего спуска, то, очевидно, потребуется не более двух шагов для отыскания х*.
- находится из условия исчерпывающего спуска, то, очевидно, потребуется не более двух шагов для отыскания х*.

Того же результата можно достичь и другим способом. Выберите некоторое направление p и две точки х
и две точки х и у
и у такие, чтобы векторы х
такие, чтобы векторы х -у
-у и p
и p были неколлинеарны. Выполнив исчерпывающий спуск из точек х
были неколлинеарны. Выполнив исчерпывающий спуск из точек х и у
и у в направлении p
в направлении p , получив точки х
, получив точки х и у
и у .
.
По свойству исчерпывающего спуска в точках х и у
и у имеет место касание соответствующих прямых (направлений убывания) и эллипсов (линий уровня целевой функции). Точки х*, х
имеет место касание соответствующих прямых (направлений убывания) и эллипсов (линий уровня целевой функции). Точки х*, х и у
и у расположены на одной прямой.
расположены на одной прямой.
Поэтому, полагая p =х
=х -у
-у и решая задачу f(х
и решая задачу f(х +
+ p
p )→min, мы находим точку х*. Таким образом, и в этом случае решение задач min-ии квадратичной сильно выпуклой функции будет получено законченное число шагов.
)→min, мы находим точку х*. Таким образом, и в этом случае решение задач min-ии квадратичной сильно выпуклой функции будет получено законченное число шагов.
Определение направления p в процессе min-ии сильно выпуклой квадратичной функции двух переменных:
в процессе min-ии сильно выпуклой квадратичной функции двух переменных:

Рассмотренному методу min-ии квадратичной функции двух переменных соответствует алгоритм:
|
|
|
ШАГ 0:
Выбрать начальную точку х ЄЕ
ЄЕ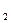 .
.
ШАГ1:
Положить p =е
=е . Найти точку х
. Найти точку х с помощью исчерпывающего спуска из точки х
с помощью исчерпывающего спуска из точки х по направлению p
по направлению p :
:
f(х )=min
)=min f(х
f(х +
+ p
p )
)
ШАГ2:
а) положить у =х
=х + е
+ е ;
;
б) найти точку у из условия исчерпывающего спуска из точки у
из условия исчерпывающего спуска из точки у по направлению p
по направлению p :
:
f(у )=min
)=min f(у
f(у +
+ p
p );
);
в) положить p =х
=х -у
-у , найти точку х
, найти точку х из условия f(х
из условия f(х )=min
)=min f(х
f(х +
+ p
p ), вычисления закончить, положив х*=х
), вычисления закончить, положив х*=х
В данном алгоритме поиск точки min-ма проводится по так называемым сопряженным направлениям.
Определение:
Ненулевые векторы p …p
…p называется сопряженным относительно матрицы А размера (n*n), если
называется сопряженным относительно матрицы А размера (n*n), если
<Аp , p
, p >=0, i=j; I,j=1,…,k (2)
>=0, i=j; I,j=1,…,k (2)
Лемма 1: Система из n векторов p …p
…p , сопряженных относительной положительно определенной матрицы А, линейно независима (или назыв. А – ортогональными).
, сопряженных относительной положительно определенной матрицы А, линейно независима (или назыв. А – ортогональными).
Таким образом, n ненулевых А-ортогональных векторов образуют базис в En.
Рассмотрим min-ию в Еn квадратичной функции f(x)=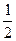 <Ax,x>+<b,x>+c с положительно определенной матрицей А с помощью итерационного процесса
<Ax,x>+<b,x>+c с положительно определенной матрицей А с помощью итерационного процесса
х =х
=х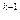 +
+ p
p , k=1,2… (3)
, k=1,2… (3)
где векторы p А – ортогональны.
А – ортогональны.
Лемма 2: Если в итерационном процессе (3) на каждом шаге используется исчерпывающий спуск, то величина шага  будет:
будет:
 =-
=- , k=1,2,… (4)
, k=1,2,… (4)
Теорема:
Последний исчерпывающий спуск по А-ортогональным направлениям (3) приводит к точке min-ма квадратичной функции не более чем за n-шагов.
Вопрос о нахождении базиса из А-ортогональных векторов в пространстве Еn решается неоднозначно. В качестве такого базиса можно взять ортогональный базис из собственных векторов матрицы А.
Однако поиск особенно при n>2 представляет собой самостоятельную довольно сложную задачу.
Итерационный процесс (1) можно организовать и без предварительного построения векторов p …p
…p , последовательно находя их в процессе min-ии.
, последовательно находя их в процессе min-ии.
Опишем процедуру метода сопряженных направлений для min-ии функции n-переменных, обобщающую приведенному выше алгоритму для n=2.
ШАГ 0:
Выбрать начальную точку х ЄЕ
ЄЕ .
.
|
|
|
ШАГ1:
Положить p =е
=е . Найти точку х
. Найти точку х из условия
из условия
f(х )=min
)=min f(х
f(х +
+ p
p )
)
ШАГ2:
а) положить у =х
=х + е
+ е ;
;
б) найти точку у из условия:
из условия:
f(у )=min
)=min f(х
f(х +
+ p
p );
);
в) положить p =х
=х -у
-у , найти точку х
, найти точку х из условия f(х
из условия f(х )=min
)=min f(х
f(х +
+ p
p ).
).
ШАГ3:
а) положить у =х
=х + е
+ е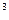 ;
;
б) найти у , минимизируя f(x) последовательно по направлениям p
, минимизируя f(x) последовательно по направлениям p и p
и p , начиная из точки у
, начиная из точки у ;
;
в) положить p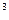 =х
=х -у
-у , найти точку х
, найти точку х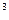 из условия f(х
из условия f(х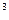 )=min
)=min f(х
f(х +
+ p
p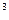 ).
).
ШАГn:
а) положить у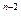 =х
=х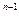 +е
+е ;
;
б) найти точку у , минимизируя f(x) последовательно по направлениям p
, минимизируя f(x) последовательно по направлениям p ,…,p
,…,p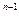 , начиная из точки у
, начиная из точки у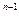 ;
;
в) положить p =х
=х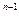 -у
-у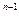 , найти точку х
, найти точку х из условия f(х
из условия f(х )=min
)=min f(х
f(х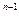 +
+ p
p ).
).
Замечание:
Как и в двумерном случае можно показать, что направления p ,…,p
,…,p , построенные при выполнении этого алгоритма, являются А-ортогональными. Поэтому, если f(x) является квадратичной функцией с положительно определенной матрицей А и все задачи одномерной min-ии решаются точно, то х*=х
, построенные при выполнении этого алгоритма, являются А-ортогональными. Поэтому, если f(x) является квадратичной функцией с положительно определенной матрицей А и все задачи одномерной min-ии решаются точно, то х*=х и вычисления на этом этапе завершаются. Если ее f(x) не является квадратичной функцией или вспомогательные задачи одномерной min-ии решаются приближенно, то необходимо перейти к следующему шагу.
и вычисления на этом этапе завершаются. Если ее f(x) не является квадратичной функцией или вспомогательные задачи одномерной min-ии решаются приближенно, то необходимо перейти к следующему шагу.
ШАГn+1 (проверка):
Если ||х -х
-х ||
||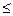
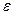 , где
, где 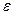 - параметр точности, то поиск завершить, полагая х*=х
- параметр точности, то поиск завершить, полагая х*=х , иначе положить х
, иначе положить х =х
=х и перейти к шагу 1.
и перейти к шагу 1.
Метод сопряженных направлений относится к числу наиболее эффективных прямых методов. Недостатком является необходимость решать довольно большое количество задач одномерной min-ии
|
|
|
|
Дата добавления: 2014-01-07; Просмотров: 865; Нарушение авторских прав?; Мы поможем в написании вашей работы!