Понятие устойчивости системы

УСТОЙЧИВОСТЬ ЛИНЕЙНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ

Все рассмотренные выше типовые динамические звенья являются минимально-фазовыми, кроме звена чистого запаздывания.

Понятие устойчивости САУ связано с способностью системы возвращаться в состояние равновесия после исчезновения внешних сил, которые вывели ее из этого состояния. Система считается устойчивой, если будучи выведенной из состояния равновесия, возвращается к этому состоянию, после снятия причин, вызвавших отклонение. Система неустойчива, если она не возвращается в состояние равновесия, из которого ее вывели, а отдаляется от него.

Введем понятия: устойчивость в малом и устойчивость в большом. Система устойчива в малом, если она устойчива при бесконечно малых возмущениях. С истема устойчива в большом, если она устойчива при всех возмущениях, возможных в системе.

Запишем выходную переменную в виде:

, (4.1)

где y_пер(t) – переходная составляющая; y_уст(t) – установившаяся составляющая. Система будет устойчива, если с течением времени при t® ¥ переходная составляющая будет стремиться к нулю, т.е. y_пер(t)=0. Причем устойчивость системы всегда закладывается в систему на этапе проектирования.

Дифференциальное уравнение САР при нулевых начальных условиях имеет вид:

(4.2)

Для оценки устойчивости САР исследуется свободная составляющая решения уравнения (4.2), т.е. решение однородного дифференциального уравнения вида:

, (4.3)

которое оценивает свободное движение системы. Данное уравнение, записанное в операторной форме

(4.4)

представляет собой характеристическое уравнение системы, корни которого p₁, p₂, …, p_n определяют характер переходного процесса. Решение однородного дифференциального уравнения имеет вид:

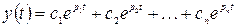, (4.5)

где с₁, с₂,…, с_п - постоянные интегрирования, определяемые из начальных условий. При этом корни характеристического уравнения определяются только видом левой части уравнения (4.2), а постоянные интегрирования определяются также и правой частью уравнения (4.2). Другими словами, быстрота затухания и форма переходного процесса определяются и левой и правой частью исходного дифференциального уравнения (4.2).

Дата добавления: 2014-01-07