Правила. Интересные конъюнктивные вопросы сами по себе определяют отношения

Интересные конъюнктивные вопросы сами по себе определяют отношения. Вопрос отец(аран,X),мужчина(X)? выражает свойство быть сыном Арана. Вопрос отец(фарра,X),отец(X,Y)? относится к внукам Фарры. Так мы приходим к третьему и самому важному виду утверждения в логическом программировании – к правилу, позволяющему определять новые отношения в терминах существующих отношений.

Правила – это утверждения вида

A ¬ B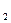,B,…B

где n≥ 0. A называется заголовком правила, а последовательность B– телом правила. Как A, так и B; должны быть целями. Правила, факты и вопросы называются также хорновыми предложениями или просто предложениями. Заметим, что факт – это частный случай правила при n =0. Факты называются также единичными предложениями. Кроме того, имеется специальное название для правил, тело которых состоит из одной цели, т.е. для случая n = 1. Такие предложения называются итерационными предложениями. В правилах, как и в фактах, переменные связаны кванторами общности, область действия кванторов – все правило.

Правило, выражающее свойство быть сыном:

сын(X,Y)¬отец(Y,X),мужчина(X)

Аналогично можно определить свойство быть дочерью:

дочь(Х,Y) ¬ отец(Y,Х),женщина(Х).

Правило для отношения быть дедушкой:

дедушка(Х,Z) ¬ отец(Х,Y),отец(Y,Z).

Возможны два способа интерпретации правил. При первом правила используются для построения новых и сложных вопросов в терминах простых вопросов. Вопрос сын(X,аран)? в программе, содержащей приведенное выше правило для отношения сын, переводится в соответствии с этим правилом в вопрос отец(аран,X),мужчина(X)? и решается как и раньше. Новый вопрос, включающий отношение сын, строится из простых вопросов, содержащих отношения отец и мужчина. Такая интерпретация правил сводится к процедурному истолкованию правил. Процедурное истолкование правила для отношения дедушка состоит в следующем: «Для ответа на вопрос, является ли X дедушкой Y ответьте на конъюнктивный вопрос, является.ли X отцом Z и Z отцом Y».

Второй способ основан на интерпретации правил как логических аксиом. Обратная стрелка ¬ используется для обозначения логического следования. Правило для отношения сын понимается так: «X – сын Y если Y – отец X и Х – мужчина». Здесь правила используются для построения новых или сложных отношений на основе других, более простых отношений. Предикат сын определяются через предикаты отец и мужчина. Соответствующее понимание правила известно как декларативное понимание. Декларативное понимание правила для отношения дедушка состоит в следующем: «Для всех X, Y и Z, если X – отец Z и Z – отец Y, то Х – дедушка Y».

Хотя формально все переменные в предложении связаны квантором общности, мы будем иногда говорить о переменных, входящих лишь в тело, а не в заголовок предложения, как если бы они были связаны в теле квантором существования. Например, правило для отношения дедушка можно понимать так: «Для всех X и Y, Х – дедушка Y, если найдется такое Z, что Х – отец Z и Z – отец Y». Мы не приводим обоснования подобной словесной трансформации и рассматриваем ее как некоторое удобство чтения.

Для введения правил в наше рассмотрение логического вывода потребуется закон modus ponens. Modus ponens утверждает, что из В и A ¬ В следует A.

· Определение. Обобщенный закон modus ponens утверждает, что из правила

R=(A ¬ B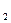,B,…B) и фактов

B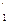

B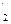

...

B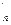

выводится A' при условии, что

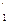A¬B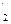,B,…,B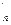

является примером R.·

Правила совпадения и конкретизации являются частными случаями обобщенного закона modus popens.

Теперь все готово для полного определения понятия логической программы и соответствующего понятия логического следствия.

· Определение. Логическая программа – это конечное множество правил.·

· Определение. Цель G с кванторами существования является логическим следствием программы Р, если в Р найдется такое предложение с основным примером A ¬ B,B,…B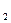, n³0, B,…,B – логические следствия Р и A – пример G. ·

Заметим, что цель С логически следует из программы Р тогда и только тогда, когда G может быть выведена из Y с помощью конечного числа применений обобщенного правила modus ponens.

Рассмотрим вопрос сын(S,аран)? относительно программы 1.1, расширенной правилом для отношения сын. Применение подстановки {X = лот, Y = аран } к данному правилу приводит к примеру сын(лот,аран) ¬ отец(аран,лот), мужчина(лот). Обе цели в теле правила являются фактами программы 1.1. Таким образом, из обобщенного modus ponens следует ответ S = лот.

Процедура поиска ответа на вопрос отражает определение логического следования. Угадываются основной пример цели и основной пример правила, далее рекурсивно ищется ответ на конъюнктивный вопрос, соответствующий телу этого правила. Доказательство цели A в программе Р сводится к выбору правила A ¬ B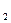,B,…B в P и указанию такой подстановки Q, что A = AQ и BQ – основные цели при 1£ i £ l. Далее рекурсивно доказывается каждая цель BQ. В такой процедуре могут возникать сколь угодно длинные цепочки доказательств. В общем случае угадать нужный основной пример и выбрать должное правило сложно.

Правило, сформулированное для описания отношения сын, корректно, но не является полным описанием соответствующего понятия. Мы не сможем, например, заключить, что Исаак был сыном Сары. Не было указано, что ребенок является сыном, как отца, так и матери. Можно добавить новое правило, описывающее данное понятие, а именно:

сын(Х,Y) ¬ мать (Y,X),мужчина (X).

Аналогично определение отношения внук требует четырех правил, включающих оба случая – отец и мать:

внук (X, Y) ¬ отец (Y, Z),отец (Z, X).

внук(Х, Y) ¬ отец(Y, Z),мать(Z, X).

внук(Х, Y) ¬ мать(Y,Z),отец(Z, X).

внук(Х, Y) ¬ мать(Y, Z), мать(Z, Х).

Имеется лучший, более компактный способ задания этих правил. Нам нужно задать отношение родитель, подходящее для отца и для матери. Частично искусство логического программирования и состоит в определении промежуточных предикатов, дающих полную и изящную аксиоматизацию некоторого отношения. Правило, описывающее отношение родитель, строится непосредственно, исходя из того, что родитель является или отцом, или матерью. Логические программы могут включать альтернативные определения или, более формально, – дизъюнкцию, применяя альтернативные правила, как в случае отношения родитель:

родитель(Х, Y) ¬ отец(Х, Y).

родитель(Х, Y) ¬ мать(Х, Y).

Правила для отношений сын и внук теперь запишутся так:

сын(Х, Y) ¬ родитель (Y, X), мужчина (X).

внук(X, Y) ¬ родитель(Y, Z),родитель(Z, X)

Совокупность правил с одним и тем же предикатом в заголовке, такая, как пара правил для родителей, называется процедурой. Позже мы увидим, что при операционной интерпретации этих правил в Прологе подобные наборы правил действительно аналогичны процедурам или подпрограммам в традиционном программировании.

Дата добавления: 2014-01-07