
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Распределение Максвелла- Больцмана
|
|
|
|
Распределение молекул идеального газа по энергиям.
Полная энергия молекулы газа складывается из суммы кинетической 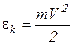 и потенциальной
и потенциальной 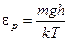 энергий. Распределение молекул газа по кинетическим энергиям описывается распределением Максвелла, а по потенциальным энергиям – распределением Больцмана. Если объединить эти распределения, то получим распределение молекул идеального газа по полным энергиям -
энергий. Распределение молекул газа по кинетическим энергиям описывается распределением Максвелла, а по потенциальным энергиям – распределением Больцмана. Если объединить эти распределения, то получим распределение молекул идеального газа по полным энергиям -  .
.
Ранее было сказано, что вероятность попадания молекул в заданный интервал кинетической энергии вблизи определенной энергии равно произведению функции распределения молекул по кинетическим энергиям на величину интервала энергий:
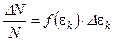 , следовательно,
, следовательно, 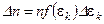 . Учитывая, что
. Учитывая, что 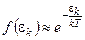 и
и 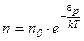 , получим:
, получим:  или
или 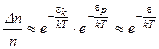 .
.
Тогда, функция распределения молекул идеального газа по полным энергиям имеет вид (без учета коэффициентов) Рис.13:
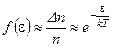 (4.26)
(4.26)

Полученное уравнение позволяет сделать ряд выводов. Во-первых, спектр возможных значений энергий молекул сплошной – т.е. разрешены любые энергии. Во-вторых, идеальный газ – это система, состоящая из очень большого числа частиц – статистический ансамбль. Все молекулы газа различимы – для каждой можно определить скорость, импульс, энергию. По найденным значениям рассчитывают средние скорости, импульсы, энергии, которые и характеризуют весь ансамбль в целом. Поскольку вероятность нахождения молекул газа максимальна на энергиях вблизи нуля (Рис.13), то можно утверждать, что количество мест на этих энергиях значительно больше, чем число частиц.
Газ, для которого:
1. частицы различимы;
2. спектр разрешенных энергий сплошной;
3. количество энергетических мест значительно больше числа частиц (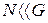 )
)
подчиняется распределению Максвелла-Больцмана и называется невырожденным газом.
|
|
|
Таким образом, доля молекул идеального газа, попадающих в заданный интервал энергий вблизи определенной энергии (т.е. вероятность их нахождения на этих энергиях), меняется по экспоненциальному закону. Чем выше энергия, тем меньше вероятность нахождения молекул на этих энергиях.
|
|
|
|
|
Дата добавления: 2014-01-07; Просмотров: 436; Нарушение авторских прав?; Мы поможем в написании вашей работы!