Случайные погрешности измерений

Как уже отмечалось, случайная погрешность - составляющая погрешность измерения, которая при повторных измерениях в одних и тех же условиях изменяется случайным образом, без видимой закономерности. Случайная погрешность является следствием случайных процессов, протекающих в измерительных цепях. Поэтому погрешность результата измерения в общем случае надо рассматривать как случайную величину.

Для оценки этих погрешностей и разработки способов уменьшения их влияния на результат измерения используют аппарат теории вероятностей и математической статистики.

В зависимости от меры ограничения числа возможных значений, которые принимаются случайной величиной, различают дискретные и беспрерывные случайныевеличины.

Случайные величины, которые принимают конечное множество возможных значений, называются дискретными.

Случайные величины, возможные значения которых беспрерывно заполняют некоторый промежуток, называются беспрерывными случайными величинами.

Возможные значения дискретных случайных величин могут быть заранее представлены. Возможные значения беспрерывных величин не могут быть заранее представлены и беспрерывно заполняют некоторый промежуток.

Для дискретной случайной величины Х каждому ее значению х можно поставить в соответствие вероятность Р(Х=х_i)=р_i того, что вследствие проведения эксперимента случайная величина Х примет заведомо заданное значение х_i из определенного множества.

Поскольку вследствие проведения эксперимента случайная величина примет одно возможное значение из заданного множества, то вероятность попадания значения случайной величины в определенное множество значений, будет равняется 1. Это есть сумма вероятностей:

Σр_i = 1

Эту суммарную вероятность можно трактовать как то, что она каким-то образом распределена между отдельными значениями. Случайная величина будет полностью описана с какой-либо (возможной) точки зрения, если задать распределение.

Этим мы установим так называемый закон распределения случайной величины.

Законом распределения дискретной случайной величины называется всякое соотношение, которое устанавливает связь между возможными значениями случайной величины и соответствующими им вероятностями.

Простейшей формой задачи этого закона есть таблица, в которой представлены возможные значения случайной величины и соответствующие им вероятности:

Х	x1	x2	x3	…	xn
Р	p1			…

Такую таблицу называют рядом распределения случайной величины.

Однако эта характеристика не является универсальной; она существует только для “прерывных” случайных величин. Для беспрерывной случайной величины не существует ряда распределения в том значении, в котором он существует для “прерывной” величины.

Однако различные области возможных значений случайной величины не могут иметь одинаковую вероятность, и для беспрерывной величины существует "распределение вероятностей", хотя и не в том значении, как для дискретной.

Для количественной характеристики этого распределения вероятностей удобно воспользоваться не вероятностью события Х=х, а вероятностью события Х<х, где х - некоторая текущая переменная.

Вероятность этого события зависит от х, т.е. является функцией от х. Эта функция носит название функции распределения случайной величины Х и обозначается F(х):

F(х) = Р(X < х)

Функцию распределения F(х) иногда называют интегральной функцией распределения или интегральным законом распределения.

Функция распределения - самая универсальная характеристика случайной величины. Она существует для всех случайных величин: как дискретных, так и беспрерывных.

Общие свойства функции распределения:

1. Функция распределения F(х) является неубывающей функцией

своего аргумента, т.е. при x₂ > x₁ F(x₂) > F(x₁).

2. На минус бесконечности функция распределения равняется нулю:

F(- ∞) = 0

3. На плюс бесконечности функция распределения равняется единице:

F(+∞) = 1

4. Вероятность попадания случайной величины на заданный участок равна приросту функции распределения на этом участке:

Р(а≤X < b) = F(b) - F(a)

5. Вероятность любого отдельного значения беспрерывной величины равна нулю. Но это не означает, что это событие (появление произвольного значения) не будет иметь место. Из этого утверждения следует только, что при неограниченном повторении опыта это событие будет появляться сколь угодно редко.

6. Функция распределения любой “прерывной” случайной величины всегда есть прерывистая ступенчатая функция, скачки которой происходят в точках, соответствующих возможным значением случайной величины, и равные (скачки) вероятностям этих значений. Сумма всех скачков функции F(х) равна единице.

7. Функция распределения беспрерывной случайной величины представляет собой функцию, беспрерывную во всех точках.

Поскольку погрешность измерения представляется в виде беспрерывной случайной величины, дальше будем рассматривать только характеристики беспрерывных случайных величин.

Для беспрерывных случайных величин существует такая характеристика как плотность распределения f(х), определяемая зависимостью:

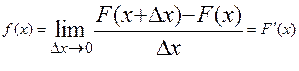
Функцию f(х) называют также "дифференциальной функцией распределения" или "дифференциальным законом распределения" величины Х.

Основные свойства плотности распределения:

1. Плотность распределения есть неотрицательная функция:

f(х) ≥ 0

2. Интеграл в бесконечных границах от плотности распределения равен единице

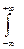f(х) dx = 1

3. Вероятность попадания величины Х на отрезок от а до b через плотность распределения определяется как

Р(а≤ X < b) = 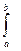f(x)dx

Значение х=х_м, при котором плотность распределения имеет максимум, называется модой. М₀

(Мода – это вариант, имеющий наибольшую частоту).

Значение М_е, для которого Р(Х<М_е)= Р(X>М_е) называется медианой случайной величины Х.

(Медиана – значение признака, приходящегося на середину ряда).

Многомерное распределение совокупности случайных величин.

Характеристикой совокупности случайных величин служит n-мерная интегральная функция распределения

F (x₁, x₂,..., х_n).

В этом случае n-мерная интегральная функция распределения равна вероятности объединения системы событий:

случайная величина Х₁ находится ниже уровня х₁, случайная величина Х₂ находится ниже уровня х₂ и т.д., т.е.

F (X₁≤x₁, X₂≤x₂,...., X_n≤x_n) = F (x₁, x₂,..., х_n).

Случайные величины Х₁, Х₂,...Х_n называются взаимно независимыми, если

F (x₁, x₂,..., х _n) = 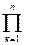F (х _к),

где F(х_к) - интегральная функция распределения случайной величины Х.

Интегральная функция распределения выражается через плотность вероятности с помощью n-кратного интеграла

F_n (x₁, x₂,..., х_n) = 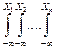f_n(x₁, x₂,..., х_n)dx₁dx₂.. dx_n

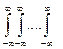f_n(x₁, x₂,..., х_n)dx₁dx₂.. dx_n = 1

Интегральная функция распределения и плотность вероятности дают полную характеристику случайной величины. Однако в ряде случаев достаточно знать о случайной величине намного меньше, можно иметь о ней лишь некоторое общее представление.

В теории вероятностей числовыми характеристиками случайных величин служат начальные моменты распределения k-того порядка (k = 1, 2,...).

Для случайной величины начальный момент k-того порядка определяются по формуле

m_к{X} = 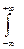х^k f (х)dx

Символ m_к{X} означает не функцию случайной величины Х, а операцию усреднения величины Х^k по множеству ее возможных значений.

Простейшая числовая характеристика случайной величины - момент распределения первого порядка, который определяет абсциссу центра тяжести плоской фигуры, ограниченного кривой плотности распределения и осью абсцисс, называется математическим ожиданием или средним значением случайной величины:

m₁{X} = 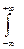х f(х)dx

Среднее значение случайной величины характеризует только расположение кривой плотности распределения. Размерность среднего значения совпадает с размерностью значений случайной величины.

Отклонение случайной величины Х от ее математического ожидания

Х₀ = Х - m {X}

называется центрированной случайной величиной.

Моменты распределения центрированной случайной величины называются центральными и обозначаются μ_k (X).

Важнейшим моментом распределения центрированной случайной величины является дисперсия, которая определяется как центральный момент второго порядка:

D{X} = 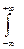[х-m(X)]² f (х)dx

Дисперсия случайной величины – характеристика рассеяния, разброса значений случайной величины возле ее математического ожидания. Само слово "дисперсия" означает "рассеяние". Размерность дисперсии совпадает с размерностью квадрата значений случайной величины.

Для наглядной характеристики рассеяния удобнее пользоваться величиной, размерность которой совпадает с размерностью случайной величины. Для этого из дисперсии извлекают квадратный корень. Полученная величина называется среднеквадратичным или стандартным отклонениям случайной величины Х от ее среднего значения:

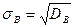
Отношение отклонения случайной величины к стандартному отклонению называется нормированным отклонением случайной величины.

В практике чаще за все имеют дело с нормальным и равномерным распределениями погрешности.

Случайная величина распределена нормально, если ее плотность распределения имеет вид:

где σ - среднеквадратичное отклонение, m(x) = m₁{Х} - математическое ожидание.

Математическое ожидание m(x) случайной величины Х является постоянной величиной и характеризует ее среднее значение.

Величина ∆=Х–m₁[X] является случайной погрешностью. Если систематическая погрешность отсутствует, то математическое ожидание равняется истинному значению величины Х.

Эти значения и среднеквадратичное отклонение полностью характеризуют нормальный закон распределения.

Дисперсия и среднеквадратичное отклонение характеризуют точность измерения: чем они больше, тем меньше точность.

(Приведенный выше закон распределения является одномерным и справедлив при одиночных измерениях.

При использовании совокупности измерений наиболее полную характеристику случайных величин дает многомерный закон распределения.)

Кроме нормального распределения для характеристики погрешностей часто используют равномерное распределение.

Примером случайной погрешности, которая имеет равномерное распределение, является погрешность отсчета по шкале прибора.

Равномерное распределение принимают часто, если закон распределения неизвестен.

Моды равномерный закон не имеет.

Математическое ожидание случайной величины, распределенной согласно равномерному закону, определится как:

m₁{Х} = (а + b)/2

Дата добавления: 2014-01-20