
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Примеры конформных отображений
|
|
|
|
Пусть функция 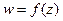 определена в некоторой окрестности точки z0.
определена в некоторой окрестности точки z0.
Определение 1. Отображение 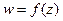 называется конформным в точке z0, если оно обладает свойствами сохранения углов и постоянства растяжений в точке z0.
называется конформным в точке z0, если оно обладает свойствами сохранения углов и постоянства растяжений в точке z0.
Пусть функция f(z) однолистная в конечной области E.
Определение 2. Отображение 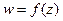 называется конформным в области E, если оно конформно в каждой точке этой области.
называется конформным в области E, если оно конформно в каждой точке этой области.
Очевидно, линейная функция 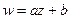 (b и a ¹ 0 – комплексные числа) осуществляет конформное отображение всей комплексной плоскости z на комплексную плоскость w. Ради наглядности совместим эти плоскости так, чтобы начала и оси координат совпадали. Тогда в частности w = z + z0 осуществляет сдвиг всей плоскости на вектор z0,
(b и a ¹ 0 – комплексные числа) осуществляет конформное отображение всей комплексной плоскости z на комплексную плоскость w. Ради наглядности совместим эти плоскости так, чтобы начала и оси координат совпадали. Тогда в частности w = z + z0 осуществляет сдвиг всей плоскости на вектор z0, 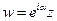 (a - действительное) – поворот плоскости вокруг начала координат на угол a, а w = kz (k > 0) – преобразование подобия, k – коэффициент подобия. Записав линейную функцию в виде
(a - действительное) – поворот плоскости вокруг начала координат на угол a, а w = kz (k > 0) – преобразование подобия, k – коэффициент подобия. Записав линейную функцию в виде 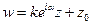
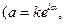
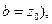 видим, что ее можно представить как произведение операций сдвига, подобия и вращения. Т. к. при этих операциях свойства сохранения углов и постоянства растяжений очевидны, то это отображение конформно.
видим, что ее можно представить как произведение операций сдвига, подобия и вращения. Т. к. при этих операциях свойства сохранения углов и постоянства растяжений очевидны, то это отображение конформно.
Углом между прямыми, проходящими через бесконечно удаленную точку, называют угол между образами этих кривых при отображении 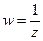 в точке w = 0.
в точке w = 0.
Например, оси декартовой системы координат пересекаются в нуле под углом 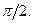 Поскольку на расширенной комплексной плоскости бесконечно удаленная точка одна, то оси пересекаются и в бесконечно удаленной точке
Поскольку на расширенной комплексной плоскости бесконечно удаленная точка одна, то оси пересекаются и в бесконечно удаленной точке 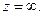 При отображении
При отображении 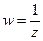 оси координат отображаются сами в себя (плоскости z и w совмещены) и, следовательно, в бесконечно удаленной точке они пересекаются также под углом
оси координат отображаются сами в себя (плоскости z и w совмещены) и, следовательно, в бесконечно удаленной точке они пересекаются также под углом 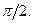
Определение 2 распространяют на любую область расширенной комплексной плоскости. Если доопределить линейную функцию, полагая 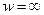 при
при 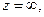 то можно убедиться, что она конформно отображает расширенную комплексную плоскость z на расширенную комплексную плоскость w.
то можно убедиться, что она конформно отображает расширенную комплексную плоскость z на расширенную комплексную плоскость w.
|
|
|
Отметим свойства функции f (z), которыми она должна обладать, чтобы отображение, осуществляемое ею, было конформным.
Теорема 1. Если функция f (z) однолистная в области Е расширенной комплексной плоскости и аналитическая всюду за исключением быть может одной точки 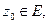 в которой
в которой 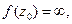 но
но 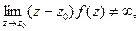 то отображение w = f(z) области Е на область G значений функции конформно (без доказательства).
то отображение w = f(z) области Е на область G значений функции конформно (без доказательства).
Рассмотрим дробно-линейную функцию 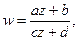
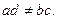 При с = 0 она переходит в линейную, рассмотренную выше, поэтому положим с ¹ 0. Дробно-линейная функция однолистная на всей комплексной плоскости, т. к. обратная функция
При с = 0 она переходит в линейную, рассмотренную выше, поэтому положим с ¹ 0. Дробно-линейная функция однолистная на всей комплексной плоскости, т. к. обратная функция 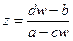 однозначная. Она аналитическая всюду, исключая точку
однозначная. Она аналитическая всюду, исключая точку 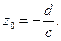 В ней она обращается в бесконечность,
В ней она обращается в бесконечность,
но 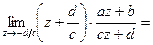
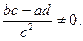
Функция удовлетворяет теореме 1 на всей комплексной плоскости, следовательно, конформна на всей комплексной плоскости. Доопределим функцию, полагая 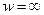 при
при 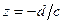 и
и 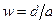 при
при 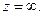 Можно убедиться, что в этом случае дробно линейная функция конформно отображает расширенную комплексную плоскость z на расширенную комплексную плоскость w.
Можно убедиться, что в этом случае дробно линейная функция конформно отображает расширенную комплексную плоскость z на расширенную комплексную плоскость w.
Справедливо и обратное утверждение, если функция конформно отображает расширенную комплексную плоскость z на расширенную комплексную плоскость w, то эта функция дробно-линейная.
Прямую на расширенной комплексной плоскости будем считать окружностью бесконечного радиуса. Можно доказать, что любую окружность на расширенной комплексной плоскости дробно-линейная функция отображает на окружность, а полуплоскость – в круг. При этом всякое дробно-линейное отображение полуплоскости 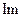 z > 0 на круг
z > 0 на круг 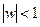 имеет вид
имеет вид
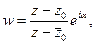 (1)
(1)
где Im z 0>0, a - действительное.
Рассмотрим функцию
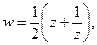 (2)
(2)
которую называют функцией Жуковского.
Функция (2) определена и однозначна на всей комплексной плоскости (исключая точку z = 0), но не однолистна на ней, т. к. обратная функция 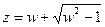 неоднозначная. Точки
неоднозначная. Точки 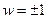 являются точками ветвления.
являются точками ветвления.
|
|
|
Найдем область однолистности. Для этого положим, что две различные точки z 1 и z 2 отображаются в одну и ту же точку w. Тогда получим
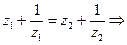
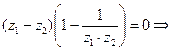
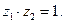
Таким образом, всякая область, не содержащая ни одной пары точек, удовлетворяющей условию 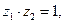 будет областью однолистности функции Жуковского. Этому условию удовлетворяет, например, круг ½ z ½< 1 или внешность этого круга ½ z ½> 1. В этих областях функция (2) удовлетворяет теореме 1 и, следовательно, отображает эти области конформно.
будет областью однолистности функции Жуковского. Этому условию удовлетворяет, например, круг ½ z ½< 1 или внешность этого круга ½ z ½> 1. В этих областях функция (2) удовлетворяет теореме 1 и, следовательно, отображает эти области конформно.
Найдем область, на которую конформно отображает функция Жуковского круг ½ z ½< 1. Положим 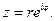 Подставляя в (2) и отделяя действительную u и мнимую v части, получим
Подставляя в (2) и отделяя действительную u и мнимую v части, получим
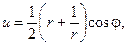
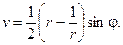
 (3)
(3)
Уравнения (3) есть уравнения эллипса с полуосями
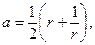
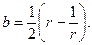 (4)
(4)
Таким образом, всякая окружность 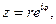
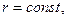
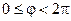 отображается в эллипсе. Из (4) следует, что при r ®1 a ®1, b ®0, т. е. граница круга ½ z ½< 1 отображается в дважды пробегаемый отрезок ½ u ½£ 1 действительной оси плоскости w. При r ®0
отображается в эллипсе. Из (4) следует, что при r ®1 a ®1, b ®0, т. е. граница круга ½ z ½< 1 отображается в дважды пробегаемый отрезок ½ u ½£ 1 действительной оси плоскости w. При r ®0 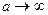 и
и 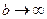 , следовательно, круг ½ z ½< 1 отображается на расширенную комплексную плоскость w с разрезом от точки z = -1 до точки z = 1 (см. рис 6¢).
, следовательно, круг ½ z ½< 1 отображается на расширенную комплексную плоскость w с разрезом от точки z = -1 до точки z = 1 (см. рис 6¢).
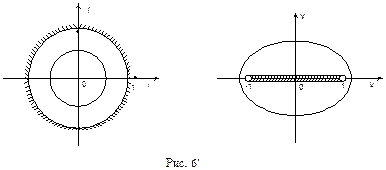
Аналогично можно убедиться, что и внешность круга ½ z ½> 1 отображается функцией Жуковского на расширенную комплексную плоскость с тем же разрезом. Таким образом, функция Жуковского отображает расширенную комплексную плоскость на поверхность Римана, состоящую из двух плоскостей склеенных по разрезу действительной оси от точки z = -1 до точки z = 1.
Основная задача теории конформных отображений заключается в нахождении функции, отображающей одну заданную область на другую заданную область. Достаточно простого алгоритма решения этой задачи не существует, поэтому на практике следует руководствоваться общими условиями существования конформного отображения и общими принципами. Перечислим важнейшие из них. Во-первых, нельзя конформно отобразить многосвязную область на односвязную, а во-вторых, нельзя всю комплексную плоскость конформно отобразить на конечную область. Однако, две произвольные односвязные области, границы которых состоят более, чем из одной точки, всегда можно конформно отобразить друг на друга.
|
|
|
Теорема 2 (принцип соответствия границ). Если функция w = f (z) конформно отображает одну область на другую, то она взаимно однозначно отображает и границы этих областей (без доказательства).
Справедлива и обратная теорема. Если функция w = f (z), аналитическая в области Е и непрерывная на ее границе, однозначно отображает эту границу на некоторую кривую Г, то функция f (z) конформно отображает область Е на область G, границей которой является кривая Г.
Пример. Найти такое конформное отображение верхней полуплоскости с разрезом по мнимой оси от точки z = 0 до точки z = i (см. рис. 7 а) на единичный круг, чтобы точка 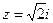 отобразилась в центр этого круга.
отобразилась в центр этого круга.
Решение. Разгладим сначала разрез. Т.к. на разрезе точки имеют аргумент p/2, то воспользуемся функцией w 1 = z 2, поскольку она удваивает аргумент точки. Эта функция аналитическая и однолистная в верхней полуплоскости и поэтому конформно отображает заданную область на плоскость w, с разрезом [-1,¥) (см. рис. б).

Согласно принципу соответствия границ ломаная ABCDA отобразится в разрез ABCDA плоскости w 1. Обозначения соответственных точек при отображении на рисунках сохранены. Буквой A обозначена бесконечно удаленная точка плоскости z (а также плоскостей w 1, w 2 и w 3).
Осуществим теперь сдвиг комплексной плоскости w 1 так, чтобы точка С попала в начало координат. Для этого воспользуемся линейным отображением w 2 = w 1 + 1 (см. рис. в).
Затем комплексную плоскость w 2 с разрезом [0,¥) отобразим на верхнюю полуплоскость. Для этого воспользуемся однозначной ветвью функции 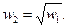 Она конформно отображает плоскость w 2 с разрезом [0,¥) на верхнюю полуплоскость w 3 (см. рис. 2).
Она конформно отображает плоскость w 2 с разрезом [0,¥) на верхнюю полуплоскость w 3 (см. рис. 2).
Наконец, полуплоскость w 3 конформно отобразим на единичный круг ½ w 4½< 1 с помощью дробно-линейной функции (см. рис. д).
Поскольку центр круга должен быть в точке E, которая на плоскости w 3 имеет координаты (0,1), то дробно-линейная функция следующая (см. (1)):
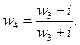
Итак, функция, осуществляющая конформное отображение заданной области на заданный единичный круг, имеет вид
|
|
|
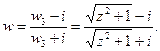
§6. Интеграл от функции комплексного переменного 
Пусть некоторая плоская кривая задана параметрически 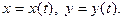 Умножая
Умножая 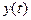 на
на 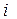 и складывая с
и складывая с 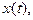 получим уравнение этой кривой в комплексном виде
получим уравнение этой кривой в комплексном виде 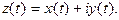 Пусть некоторая дуга
Пусть некоторая дуга 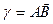 лежит на этой кривой, причем точке А на этой дуге отвечает значение параметра
лежит на этой кривой, причем точке А на этой дуге отвечает значение параметра 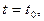 а точке В -
а точке В - 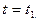

Под интегралом от функции 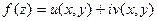 по дуге
по дуге 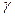 будем понимать число, определяемое следующим выражением
будем понимать число, определяемое следующим выражением
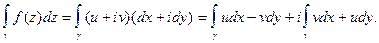 (1)
(1)
Из (1) видно, что интеграл от функции комплексного переменного определяется двумя криволинейными интегралами второго рода. Поэтому, если криволинейные интегралы второго рода существуют, то существует и интеграл от функции комплексного переменного. Все свойства криволинейного интеграла второго рода справедливы и для интеграла (1). В частности он зависит от направления движения по дуге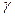 .
.
Если дуга 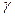 гладкая, то интеграл (1) легко сводится к определенному
гладкая, то интеграл (1) легко сводится к определенному
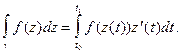 (2)
(2)
Пример 1. Найти интеграл от функции 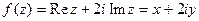
а) по отрезку прямой, соединяющей начало координат с точкой (1;1);
б) по отрезку параболы 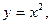 проходящей через эти точки.
проходящей через эти точки.
Решение. Запишем уравнение прямой и параболы в комплексной форме: 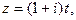
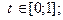
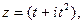
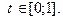
Используя (2), получим:
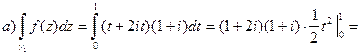
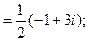
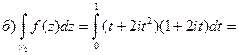
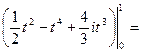
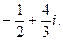
Пример 2. Вычислить 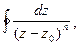 где С - окружность радиуса R c центром в
где С - окружность радиуса R c центром в 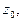 которая обходится в положительном направлении один раз, n- целое число.
которая обходится в положительном направлении один раз, n- целое число.
Решение. Запишем уравнение окружности в комплексном виде
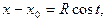
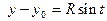
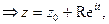
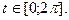
Согласно (2), имеем
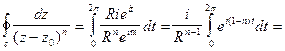
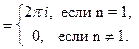
Заметим, что интеграл не зависит ни от радиуса R окружности, ни от точки 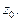
Теорема 1 (Коши). Пусть в односвязной области Е задана аналитическая функция f(z). Тогда интеграл от этой функции по любому замкнутому контуру С, целиком лежащему в области Е, равен нулю, т. е.
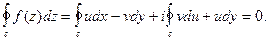 (3)
(3)
Доказательство. Воспользуемся формулой Грина
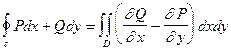 (4)
(4)
(см. §8 гл.9, ч.1). Из (3) и (4) следует
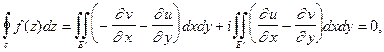
так как согласно условиям Эйлера-Даламбера подынтегральные выражения двойных интегралов обращаются в нуль. Здесь 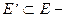 область, ограниченная контуром С. Теорема доказана.
область, ограниченная контуром С. Теорема доказана.
Замечание. Теорема Коши справедлива и в том случае, когда контур С совпадает с границей области Е, если дополнительно потребовать непрерывности функции f(z) в замкнутой области 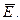
|
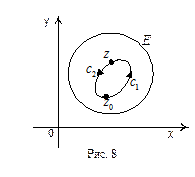
Пусть замкнутый контур С лежит в односвязной области E, в которой функция f(z) аналитическая. Пусть 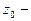 некоторая фиксированная точка, а z - текущая точка на контуре С (см. рис. 8).
некоторая фиксированная точка, а z - текущая точка на контуре С (см. рис. 8).
Тогда, согласно свойствам интеграла и теореме 1,
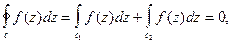
или 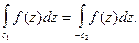 (5)
(5)
Здесь 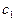 означает дугу
означает дугу 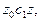
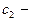 дугу
дугу 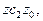 а
а 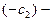 дугу
дугу 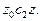 Равенство (5) означает, что значение интеграла не зависит от пути интегрирования, а только от начальной
Равенство (5) означает, что значение интеграла не зависит от пути интегрирования, а только от начальной 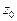 и конечной
и конечной 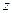 точек интегрирования:
точек интегрирования:
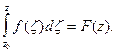 (6)
(6)
Можно убедиться, что функция 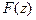 является первообразной функцией для функции
является первообразной функцией для функции 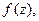 а интеграл (6) удовлетворяет всем свойствам интеграла с переменным верхним пределом от действительной функции.
а интеграл (6) удовлетворяет всем свойствам интеграла с переменным верхним пределом от действительной функции.
Пример 3. Найти интеграл 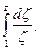
Решение. Функция 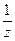 аналитическая в комплексной плоскости (z), исключая z= 0. Плоскость с разрезом по отрицательной полуоси будет односвязной областью, в которой функция
аналитическая в комплексной плоскости (z), исключая z= 0. Плоскость с разрезом по отрицательной полуоси будет односвязной областью, в которой функция 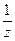 аналитическая. Тогда, согласно (6), получим
аналитическая. Тогда, согласно (6), получим  где lnz – одна из ветвей многозначной функции Lnz.
где lnz – одна из ветвей многозначной функции Lnz.
Теорема 2. Пусть функция  аналитическая в многосвязной области Е, ограниченной контурами
аналитическая в многосвязной области Е, ограниченной контурами 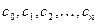 и пусть f (z) непрерывная в
и пусть f (z) непрерывная в 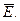 Тогда
Тогда
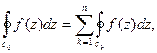 (7)
(7)
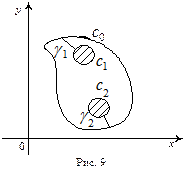
|
где 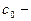 внешняя граница области E,
внешняя граница области E, 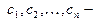 внутренние контуры, ограничивающие область Е. Все контуры обходятся против стрелки часов.
внутренние контуры, ограничивающие область Е. Все контуры обходятся против стрелки часов.
Доказательство. Соединим внешний контур 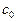 с внутренними контурами кривыми
с внутренними контурами кривыми 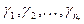 Тогда многосвязная область Е станет односвязной (см. рис. 9). Согласно теореме1 и замечанию к ней, имеем
Тогда многосвязная область Е станет односвязной (см. рис. 9). Согласно теореме1 и замечанию к ней, имеем
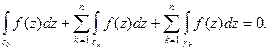 (8)
(8)
Вся граница односвязной области проходится в положительном направлении, т.е. так, что область остается слева (внешний контур 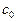 против часовой стрелки,
против часовой стрелки, 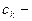 по часовой стрелке). Кривые
по часовой стрелке). Кривые 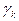 проходятся дважды в разных направлениях, поэтому сумма интегралов по этим кривым равна нулю. Меняя направление обхода внутренних контуров, получим (7). Теорема доказана.
проходятся дважды в разных направлениях, поэтому сумма интегралов по этим кривым равна нулю. Меняя направление обхода внутренних контуров, получим (7). Теорема доказана.
Теорема 3. Пусть функция  аналитическая в односвязной области Е и непрерывна в
аналитическая в односвязной области Е и непрерывна в 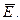 Тогда
Тогда 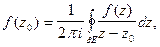 (9)
(9)
где 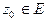 (без доказательства).
(без доказательства).
Формулу (9) называют интегральной формулой Коши.
Следствие. В условиях теоремы 3 справедлива формула
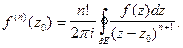 (10)
(10)
Из (10) следует, что аналитическая функция дифференцируема сколько угодно раз. Заметим, что (10) можно получить формальным дифференцированием (9) по параметру 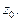
Пример 4. Вычислить 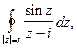 если
если 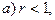
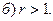
|
|
|
|
Дата добавления: 2014-01-11; Просмотров: 13834; Нарушение авторских прав?; Мы поможем в написании вашей работы!