Числовые характеристики случайных величин

Характеристики случайных величин

Среди числовых характеристик случайных величин, прежде всего, рассмотрим характеристики положения, фиксирующие положение случайной величины на числовой оси, т. е. некоторое среднее, ориентировочное значение с. в., около которого группируются ее возможные значения.

Из характеристик положения в теории вероятностей наибольшую роль играет математическое ожидание, которое иногда называют просто средним значением случайной величины.

Математическим ожиданием дискретной случайной величины называется сумма произведений всех возможных ее значений на вероятности этих значений.

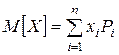. (5.17)

Для случая, когда число возможных значений дискретной с. в. X не конечно, а бесконечно (образует счетное множество), формула для математического ожидания остается той же, только в верхнем пределе суммы п заменяется на бесконечность:

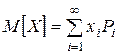. (5.18)

Для непрерывной с. в. X с плотностью f(x)

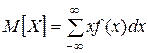. (5.19)

Среднее арифметическое значение — это частное от деления суммы полученных из опытов значений случайной величины на число слагаемых этой суммы, т. е. на число опытов.

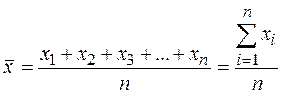, (5.20)

где 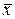— среднее арифметическое случайной величины;

n — число проведенных опытов;

х₁, х₂,..., х_N — отдельные значения случайной величины.

При увеличении числа опытов п частота события 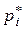будет приближаться (сходиться по вероятности) к вероятности 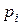этого события. Значит, и среднее арифметическое М* [X] будет приближаться (сходиться по вероятности) к математическому ожиданию М [X] случайной величины X. Это значит, что при достаточно большом числе опытов можно среднее арифметическое наблюденных значений с. в. X принимать приближенно равным ее математическому ожиданию.

Указанная выше связь между математическим ожиданием и средним арифметическим составляет содержание одной из предельных теорем теории вероятностей (так называемого закона больших чисел).

Выше мы ввели обозначение М [X] для математического ожидания с. в. X. Иногда бывает удобнее обозначить его одной буквой .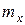

Модой случайной величины называется ее наиболее вероятное значение (то, для которого вероятность 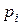или плотность распределения f(x) достигает максимума).

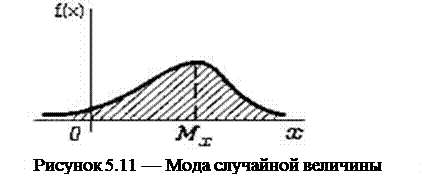
На рисунке 5.11 показана кривая распределения непрерывной с. в. X; точка, в которой плотность f(x) достигает максимума, и есть мода .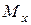

Иногда применяется еще одна характеристика положения — медиана случайной величины X, которую мы обозначим 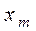. Эта характеристика применяется, как правило, только для непрерывных с. в. Медианой непрерывной случайной величины X называется такое ее значение , для которого

,

т. е. одинаково вероятно, окажется ли с. в. А меньше или больше . Геометрически медиана — это абсцисса той точки на оси Ох, для которой площади, лежащие слева и справа от нее, одинаковы и равны 1/2.

В случае симметричного распределения (имеющего моду) математическое ожидание (если оно существует), мода и медиана совпадают.

Размах рассеивания случайной величины — это разность между максимальным и минимальным ее значениями, полученными в результате испытаний.

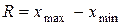. (5.21)

При малом числе наблюдений 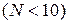размах служит мерой рассеивания.

Дисперсия является одной из основных характеристик рассеивания случайной величины около ее математического ожидания. Само слово “дисперсия” означает “рассеивание”. Величина ее определяется по формуле:

. (5.22)

Дисперсия имеет размерность квадрата случайной величины, что не всегда удобно. Для наглядности в качестве характеристики рассеивания удобнее пользоваться числом, размерность которого совпадает с размерностью случайной величины. Для этого из дисперсии извлекают квадратный корень. Полученная величина называется средним квадратическим отклонением (стандартным отклонением).

Среднее квадратическое отклонение определяется:

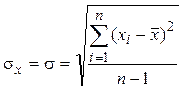. (5.23)

Для неотрицательной случайной величины X в качестве характеристики ее рассеивания иногда применяется коэффициент вариации, равный отношению стандартного отклонения к математическому ожиданию:

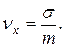(5.24)

Введение коэффициента вариации необходимо для сравнения рассеивания величин, имеющих разную размерность. Для этой цели среднее квадратичное отклонение непригодно, так как имеет размерность случайной величины.

В технической эксплуатации автомобилей различают случайные величины с малой (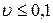), средней (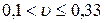) и большой вариацией ().

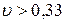(5.16)

Введем новое, очень важное понятие теории вероятностей — закон распределения.

Каждый закон распределения исчерпывающим образом описывает распределение вероятностей и дает возможность вычислять вероятности любых событий, связанных со случайной величиной.

Законом распределения случайной величины называется любое правило (таблица, функция), позволяющее находить вероятности всевозможных событий, связанных со случайной величиной (например, вероятность того, что она примет какое-то значение или попадет на какой-то интервал).

Если случайная величина X имеет данный закон распределения, то про нее говорят, что она “распределена” по этому закону (или же “подчинена” этому закону распределения).

Наиболее простую форму можно придать закону распределения дискретной случайной величины. Для этого достаточно перечислить возможные значения случайной величины X: и соответствующие им вероятности.

Рядом распределения дискретной случайной величины X называется таблица, в верхней строке которой перечислены в порядке возрастания все возможные значения случайной величины X:, а в нижней — вероятности этих значений: где — вероятность того, что в результате опыта случайная величина X примет значение 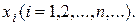Ряд распределения случайной величины X можно записать в виде таблицы:

X:			…		…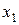
		…		…

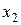
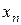
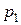
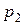
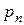
(5.5)

Так как события 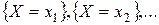несовместны и образуют полную группу, то сумма всех вероятностей, стоящих в нижней строке ряда (5.5), равна единице:

(5.6)
Эта единица как-то распределена между значениями случайной величины (отсюда и термин “распределение”).

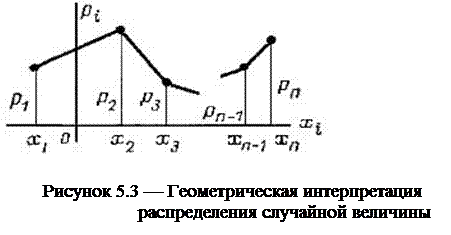
Графическое изображение ряда распределения называется многоугольником распределения. Строится он так: для каждого возможного значения случайной величины восстанавливается перпендикуляр к оси абсцисс, на котором откладывается вероятность данного значения случайной величины. Полученные точки для наглядности (и только для наглядности!) соединяются отрезками прямых (рисунок 5.3).

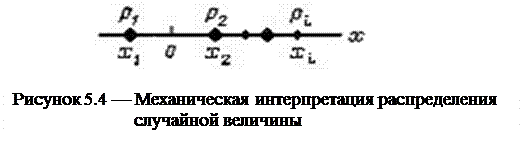
Кроме геометрической интерпретации распределения дискретной случайной величины, часто оказывается полезной и ее механическая интерпретация. Это - ряд материальных точек на оси абсцисс, имеющих абсциссы 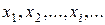и, соответственно, массы 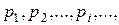в сумме образующие единицу (рисунок 5.4).

Дата добавления: 2014-01-14