
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Четвёртый этап минимизации
|
|
|
|
В некоторых случаях после получения отмеченной таблицы переходов автомата возможен четвертый этап минимизации. Правда этот этап не всегда приводит к уменьшению числа состояний и часто является проверочным. Алгоритм этого этапа рассмотрим на примере.
Пусть есть автомат, заданный следующей отмеченной таблицей переходов:
| yg | y1 | y1 | y1 | y2 | y1 | y2 | y2 | y2 |
| xj\ai | ||||||||
| x1 | ||||||||
| x2 | ||||||||
| X3 |
Алгоритм минимизации заключается в следующем:
- Все внутренние состояния разбиваются на группы по числу выходных сигналов. В нашем случае есть два выходных сигнала y 1 и y 2 и, следовательно, будет две группы, которые мы обозначим буквами a и b.

- По таблице переходов автомата определяют, к каким группам принадлежат внутренние состояния, в которые автомат переходит из данного состояния под воздействием каждой буквы входного алфавита. Эти состояния запишем в виде последовательности букв под каждым из состояний автомата. Например, из состояния 0 автомат переходит в состояния 2, 3 и 1, которые принадлежат соответственно к следующим группам a, b и a. Эта последовательность букв (aba) и записывается под состоянием 0.
- Проводят новое разделение внутренних состояний на группы, объединяя в каждой группе состояния, отмеченные одинаковой последовательностью букв. В нашем случае каждая из двух групп распадается на две группы, по числу различных последовательностей букв:
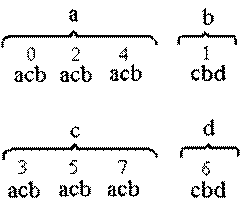
- Пользуясь таблицей переходов автомата, вновь отмечают каждое состояние последовательностью букв. Разделение состояний на новые группы продолжают до тех пор, пока новые группы состояний появляться не будут. В нашем случае, минимизация заканчивается на втором шаге, так как все состояния, входящие в группы а и с отмечены одинаковыми последовательностями букв, а группа b и d содержат только по одному состоянию.
Все состояния, входящие в каждую из этих групп, можно заменить одним состоянием той же группы. Взяв в качестве представителей групп состояния 0, 1, 3 и 6 и обозначив их символами a 0, a 1, a 2 и a 3 соответственно, получим следующую таблицу переходов с минимальным числом внутренних состояний.
|
|
|
| yg | y1 | y1 | y2 | y2 |
| xj\ai | a0 | a1 | a2 | a3 |
| x1 | a0 | a2 | a0 | a2 |
| x2 | a2 | a1 | a2 | a1 |
| x3 | a1 | a3 | a1 | a3 |
Для построения автомата Мили, воспользуемся рассмотренным ранее алгоритмом, для чего в каждую клетку >совмещенной таблицы переходов и выходов запишем значения выходного сигнала, которым отмечено, находящееся здесь состояние.
| xj\ai | a0 | a1 | a2 | a3 |
| x1 | a0/y1 | a2/y2 | a0/y1 | a2/y2 |
| x2 | a2/y2 | a1/y1 | a2/y2 | a1/y1 |
| x3 | a1/y1 | a3/y2 | a1/y1 | a3/y2 |
В полученной таблице колонки, помеченные состояниями a 0 и a 2, a 1 и a 3 идентичны, что позволяет при минимизации исключить состояния a 2 и a 3. В результате получаем таблицу переходов и выходов автомата Мили имеющего два состояния a 0 и a 1.
| xj\ai | a0 | a1 |
| x1 | a0/y1 | a0/y2 |
| x2 | a0/y2 | a1/y1 |
| x3 | a1/y1 | a1/y2 |
Раздел 6. Лекция 15. Вероятностные автоматы
Детерминированные автоматы S мы задавали совокупностью из пяти объектов: S(A, X, Y, d, l), где A = { a 0, a 1, a 2,..., a M}– множество внутренних состояний автомата, X = { x 1, x 2,…, xF } – множество входных сигналов (входной алфавит), x i – буква входного алфавита, Y = {y1, y2,…, yG} – множество выходных сигналов (выходной алфавит),
d - функция переходов, обеспечивающая однозначный переход автомата в состояние as из состояния аm под действием входного сигнала xf, то есть as = d [ am, xf ],
l - функция выходов, определяющая однозначное значение выходного сигнала yg в зависимости от состояния автомата аm и входного сигнала xf, т.е. yg = l [ аm , xf ].
|
|
|
В работе Поспелова Д.А. «Вероятностные автоматы» рассмотрена более общую модель автомата, а именно: зная состояние автомата аm и входной сигнал xf, мы не можем с вероятностью, равной 1 сказать, в каком состоянии окажется автомат в следующий момент времени, а также какой выходной сигнал он в этом случае вырабатывает. Однако мы можем указать вероятности наступления соответствующего события, а именно: зная состояние аm и входной сигнал xf, мы можем указать вероятности перехода автомата в состояния { а0, а1, …, аm, …, аM }, а также вероятности появления выходных сигналов {y1, y2,…,yg, …, yG}, т.е. задаем закон распределения вероятностей. Законы распределения задаются в виде следующих таблиц:
| am,xf | a0 | a1 | … | am | … | aM |
| a0,x1 | P010 | P011 | … | P01m | … | P01M |
| a0,x2 | P020 | P021 | … | P02m | … | P02M |
| … | … | … | … | … | … | … |
| am,xF | P0F0 | P0F1 | … | P0Fm | … | P0FM |
| a1,x1 | P110 | P111 | … | P11m | … | P11M |
| … | … | … | … | … | … | … |
| am,xf | Pmf0 | Pmf1 | … | Pmfm | … | PmfM |
| … | … | … | … | … | … | … |
| aM,xF | PMF0 | PMF1 | … | PMFm | … | PMFM |
| am,xf | y1 | y2 | … | yy | … | aM |
| a0,x1 | q011 | q012 | … | q01y | … | q01G |
| a0,x2 | q021 | q022 | … | q02y | … | q02G |
| … | … | … | … | … | … | … |
| am,xF | q0F1 | q0F2 | … | q0Fy | … | q0FG |
| a1,x1 | q111 | q112 | … | q11y | … | q11G |
| … | … | … | … | … | … | … |
| am,xf | qmf1 | qmf2 | … | qmfy | … | qmfG |
| … | … | … | … | … | … | … |
| aM,xF | qMF1 | qMF2 | … | qMFy | … | qMFG |
Т.е. в каждом случае имеем закон распределения, заданный в виде гистограмм.
Очевидно, т.к. автомат обязательно перейдет в одно из состояний, то
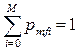 ,
, 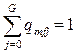 ,
,
где 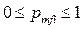 ,
, 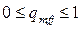 .
.
Автоматы, в которых зная состояние автомата аm и входной сигнал xf, мы можем указать лишь вероятности перехода в новое состояние и вероятности появления выходных сигналов, т.е. законы распределения, называются вероятностными автоматами (ВА).
По аналогии с детерминированными автоматами, Можно определить ВА Мили и Мура. ВА, у которых вероятности появления выходных сигналов (закон распределения) зависят лишь от состояний автомата, но не зависят от входных сигналов, называются ВА Мура. Если же вероятности появления выходных сигналов (закон распределения) зависят как от состояний автомата, так и от входных сигналов, имеем автомат Мили.
Рассмотрим некоторые частные случаи вероятностных автоматов. Может быть, что выходные сигналы автомата определяются детерминировано, а переходы автомата – случайно. Такие автоматы называются Y – детерминированными вероятностными автоматами. Если состояния определяются детерминировано, то имеем А- детерминированный вероятностный автомат.
|
|
|
Если в процессе функционирования автомата законы распределения вероятностей появления выходных сигналов и вероятности перехода автомата в новые состояния не меняются во времени, то такие ВА называются ВА с постоянной структурой.
Очевидно, можно рассмотреть общий случай, когда эти законы распределения зависят от времени. Такие автоматы называются ВА с переменной структурой.
ВА с переменной структурой в каждый фиксированный такт работы является некоторым обычным ВА, но в период между тактами ВА может изменять свои матрицы переходных вероятностей или таблицы выходных вероятностей, или и то и другое вместе.
Часто при построении ВА изменение вероятностей производят по некоторому закону, причем закон зависит от истории функционирования автомата (т.е. зависит от входных сигналов, поданных на него и от выходных сигналов, т.е. реакции автомата). Такие ВА с переменной структурой называются автоматами компенсирующего типа. Их разработке и уделяется основное внимание.
В этом случае можно сказать, что ВА работает в некоторой среде, в которую он выдает выходные сигналы и из которой он получает входные.

Входные сигналы условно можно разделить на поощрения («нештрафы») и наказания («штрафы»). При этом в зависимости от выходного сигнала на вход подается поощрение или штраф. Если в зависимости от этих сигналов менять вероятности перехода автомата из одного состояния в другое, то оказывается, что с течением времени автомат перестраивается таким образом, что он начинает с большой вероятностью получать сигналы поощрения, т.е. он в некотором смысле приспосабливается к той среде, в которой он находится.
Проблема организации целесообразного поведения автомата в случайной среде тесно связана со способом изменения вероятностей перехода автомата. Возможно изменение вероятностей перехода автомата по строкам и по столбцам.
|
|
|
Рассмотрим У-детерминированный вероятностный автомат. Пусть автомат в некоторый момент времени t находится в состоянии аm, выдал соответствующий этому состоянию выходной сигнал yg и получилна вход сигнал поощрения. Тогда вероятность р mm перехода из состоянии аm в состояние аm увеличиваются на некоторую величину  , а все остальные вероятности в строке уменьшаются на
, а все остальные вероятности в строке уменьшаются на  /М. Если же автомат получает сигнал штрафа, то вероятность р mm перехода из состоянии аm в состояние аm уменьшаются на некоторую величину
/М. Если же автомат получает сигнал штрафа, то вероятность р mm перехода из состоянии аm в состояние аm уменьшаются на некоторую величину  , а все остальные вероятности в строке на увеличиваются на
, а все остальные вероятности в строке на увеличиваются на /М, чтобы сумма вероятностей осталась равной 1.
/М, чтобы сумма вероятностей осталась равной 1.
Возможен и другой принцип изменения вероятностей, при котором происходит учет предыстории поведения автомата. Если автомат в момент времени t перешел из состояния аm в состояние ак и в момент времени t +1 получил сигнал «штраф», то вероятность р mк заменяется на  р mк, где коэффициент
р mк, где коэффициент больше 0 и меньше 1, а все остальные вероятности в строке изменяются на величину
больше 0 и меньше 1, а все остальные вероятности в строке изменяются на величину 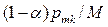 . Если же получил сигнал «нештраф», то вероятность р mк величину
. Если же получил сигнал «нештраф», то вероятность р mк величину 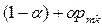 , а все остальные уменьшаются на величину
, а все остальные уменьшаются на величину  .
.
Можно менять вероятности в матрице перехода не только по строкам, но и по столбцам. Например, возможен следующий алгоритм. Если в момент времени t под влиянием входного сигнала xf автомат перешел в состояние аm и в момент времени t +1 получил сигнал «штраф», то независимо от того, из какого состояния он перешел, все элементы m-го столбца в матрице переходов заменяются на (р mm –  ) или
) или  р mm, а все остальные вероятности изменяются аналогично тому, как это происходило при изменении вероятностей по строкам.
р mm, а все остальные вероятности изменяются аналогично тому, как это происходило при изменении вероятностей по строкам.
Подобные автоматы уже находят применение при управлении в сложных системах и дают больший эффект там, где раньше работали детерминированные автоматы.
Рассмотрим пример, который приводит Д.А. Поспелов – регулирование движения через автомобильный перекресток. Обычно (мы с вами всегда сталкиваемся именно с таким светофором) задают жесткий режим переключения светофоров, при котором длительность включенных сигналов (красного и зеленого) – постоянны. Однако, как показывает практика работы таких светофоров, решение задачи получается мало эффективным, поскольку предполагается, что потоки машин постоянные, стационарные.
Можно установить датчики на перекрестке, которые бы подсчитывали число машин (очередь), возникающее в данном направлении при красном свете светофора. Пусть на перекрестке стоит ВА компенсирующего типа, который имеет 2 состояния: включен красный свет вдоль главного направления и включен зеленый свет. Каждому состоянию однозначно соответствует выходной сигнал, т.е. автомат У-детерминированный. С датчиков поступают сигналы штрафа и нештрафа.
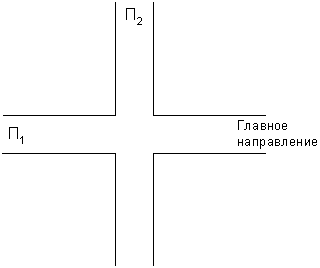
Матрица переходов выглядит следующим образом: 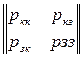 .
.
Пусть в начале все эти вероятности равны 0,5 и на главном направлении скопилось П1 машин, а на другом – П2. На вход автомата поступает сигнал 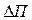 = П1 – П2. Пусть
= П1 – П2. Пусть 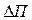 > 0, т.е. на главном направлении больше машин. Тогда если автомат в момент времени t находился в состоянии зеленом, перешел в состояние зеленый и получил сигнал нештраф, то вероятность рзз (t +1) увеличивается, а вероятность рзк (t +1) уменьшается: рзк (t +1) =
> 0, т.е. на главном направлении больше машин. Тогда если автомат в момент времени t находился в состоянии зеленом, перешел в состояние зеленый и получил сигнал нештраф, то вероятность рзз (t +1) увеличивается, а вероятность рзк (t +1) уменьшается: рзк (t +1) =  рзк (t),
рзк (t),
а вероятность рзз (t +1) = 1– рзк (t +1).
Тем самым увеличивается вероятность состояния зеленое вдоль главного направления, т.е. автомат подстраивается под обстановку. Заметим, что если потоки одинаковы, то оптимальной является следующая матрица переходов: 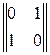 .
.
|
|
|
|
|
Дата добавления: 2014-10-31; Просмотров: 341; Нарушение авторских прав?; Мы поможем в написании вашей работы!