Проверка статистических гипотез

12.1. Основные понятия. Проверка гипотез о параметрах

нормально распределенной генеральной совокупности.

Во многих случаях результаты наблюдений используются для проверки предположений (гипотез) относительно тех или иных свойств распределения генеральной совокупности.

Пусть X - наблюдаемая дискретная или непрерывная слу­чайная величина. Статистической гипотезой H называется пред­положение относительно параметров или вида распределения слу­чайной величины X. Статистическая гипотеза Н называется про­стой, если она однозначно определяет распределение случайной величины X; в противном случае гипотеза Н называется сложной. Так, простой гипотезой является предположение о том, что слу­чайная величина X распределена по нормальному закону N (n,0).

если же высказывается предположение, что случайная величина X имеет нормальное распределение N (m,1), где а ≤ m ≤ b, то это сложная гипотеза. Примером сложной гипотезы является также предположение о том, что непрерывная случайная величина X с вероятностью 1/3 принимает значение из интервала (l,5); в этом случае распределение случайной величины X может быть любым из класса непрерывных распределений.

Бывает, что распределение случайной величины X известно, и по выборке наблюдений необходимо проверить предположения о значении параметров этого распределения. Такие гипотезы на­зываются параметрическими. Рассмотрим проверку параметриче­ских гипотез.

Проверяемая гипотеза называется нулевой гипотезой и обо­значается Н ₀. Наряду с гипотезой Н ₀ рассматривают одну из аль­тернативных (конкурирующих) гипотез Н ₁. Так, если проверяется гипотеза о равенстве параметра θ некоторому заданному значе­нию θ₀, т. е. Н ₀: θ = θ ₀, то в качестве альтернативной гипотезы можно рассмотреть одну из следующих гипотез: Н ₁ ⁽¹⁾: θ > θ ₀; Н ₁⁽²⁾: θ < θ ₀; Н ₁ ⁽³⁾: θ ≠ θ ₀; Н ₁⁽⁴⁾: θ = θ ₀, где θ ₁ - заданное значение, θ ₁ ≠ θ ₀. Выбор альтернативной гипотезы определяется конкретной формулировкой задачи.

Правило, по которому принимается решение принять или отклонить гипотезу Н ₀, называется критерием K. Так как реше­ние принимается на основе выборки наблюдений случайной величины X, необходимо выбрать подходящую статистику, называе­мую в этом случае статистикой Z критерия K. При проверке простой параметрической гипотезы Н ₀: θ = θ ₀в качестве стати­стики критерия выбирают ту же статистику, что и для оценки па­раметра θ, т.е. .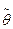

Проверка статистической гипотезы основывается на прин­ципе, в соответствии с которым маловероятные события считают­ся невозможными, а события, имеющие большую вероятность, считаются достоверными. Этот принцип реализуют так: перед анализом выборки фиксируется некоторая малая вероятность а, называемая уровнем значимости; пусть V — множество значений статистики Z, a 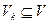- такое подмножество, что при условии истинности гипотезы Н ₀ вероятность попадания статистики кри­терия в V_k равна α, т.е. P[Z Î V_k/H₀]= α.

Обозначим z_B выборочное значение статистики Z, вычис­ленное по выборке наблюдений. Критерий формулируется сле­дующим образом: отклонить гипотезу H₀, если z_k Î V_k; принять

гипотезу H₀, если z_BÎV\V_k. Критерий, основанный на исполь­зовании заранее заданного уровня значимости, называют крите­рием значимости. Множество V_k всех значений статистики критерия Z, при которых принимается решение отклонить гипотезу H₀, называется критической областью; область V\V_k называется областью принятия гипотезы H₀.

Уровень значимости α определяет «размер» критической области V_k. Положение критической области на множестве значений статистики Z зависит от формулировки альтернативной гипотезы Н ₁. Например, если проверяется гипотеза Н ₁: θ = θ ₀, а альтернативная гипотеза Н ₁, формулируется как Н ₁: θ > θ ₀ (θ < θ ₀), то критическая область размещается на пра­вом (левом) «хвосте» распределения статистики Z, т. е. имеет вид неравенства Z > z_1-α (Z< z_α), где z_1-α и z_α - квантили распреде­ления статистики Z при условии, что верна гипотеза H₀. В этом случае критерий называется односторонним, соответственно пра­восторонним и левосторонним.

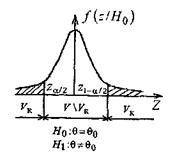
Рис. 15.

Если альтернативная гипотеза формулируется как Н ₁: θ ≠ θ ₀, то критическая область размещается на обоих «хво­стах» распределения Z, т.е. определяется совокупностью нера­венств Z <z_α/2 и Z > z_1-α/2; в этом случае критерий называется двусторонним.

На рисунке 15 показано расположение критической области V_k для различных альтернативных гипотез. Здесь f_z(z/H₀) -плотность распределения статистики Z критерия при условии, что верна гипотеза H₀,V\V_k- область принятия гипотезы, P[ZÎV\V_k] = 1 -α.

Проверка параметрической статистической гипотезы при помощи критерия значимости состоит из следующих этапов:

1) сформулировать проверяемую (H₀) и альтернативную (Н ₁) гипотезы;

2) назначить уровень значимости α;

3) выбрать статистику Z критерия для проверки гипотезы H₀;

4) определить выборочное распределение статистики Z при условии, что верна гипотеза H₀;

5) в зависимости от формулировки альтернативной гипо­тезы определить критическую область V_k одним из неравенств Z <z_α и Z > z_1-α; или совокупностью неравенств Z <z_α/2 и Z > z_1-α/2;

6) получить выборку наблюдений и вычислить выбороч­ное значение z_B статистики критерия;

7) принять статистическое решение:

если z_B Î V_K, то отклонить гипотезу Н₀ как не согласую­щуюся с результатами наблюдений;

если z_B ÎV\V_K, то принять гипотезу Н₀, т. е. считать, что гипотеза Н₀ не противоречит результатам наблюдений.

Замечание. Как правило на этапах 4) - 7) используют стати­стику, квантили которой табулированы: статистику с нормальным распределением N(0, 1 ), статистику Стьюдента, статистику 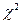или статистику Фишера. Однако интерпретацию решения и вы­числение вероятностей ошибок, допускаемых при проверке гипо­тез, удобно проводить для статистики, являющейся непосредст­венной оценкой параметра θ, т. е. статистики .

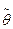Пример 50. По паспортным данным автомобильного двига­теля расход топлива на 100 км пробега составляет 10 л. В резуль­тате изменения конструкции двигателя ожидается, что расход то­плива уменьшится. Для проверки проводятся испытания 25 слу­чайно отобранных автомобилей с модернизированным двигате­лем, причем выборочное среднее расходов топлива на 100 км пробега по результатам испытаний составило = 9,3 л. Предпола­гается, что выборка расходов топлива получена из нормально распределенной генеральной совокупности со средним т и дис­персией σ ² = 4 л². Используя критерий значимости, проверить гипотезу, утверждающую, что изменение конструкции двигателя не повлияло на расход топлива.

Решение. Проверяется гипотеза о среднем (m) нормально распределенной генеральной совокупности. Проверку гипотезы проведем по этапам:

1) проверяемая гипотеза Н₀:т = 10, альтернативная ги­потеза Н ₁: т < 10;

2) выберем уровень значимости α = 0,05;

3) в качестве статистики критерия используем оценку ма­тематического ожидания - выборочное среднее ;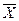

4) так как выборка получена из нормально распределен­ной генеральной совокупности, выборочное среднее также имеет нормальное распределение с дисперсией 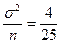. При условии, что верна гипотеза Н₀, математическое ожидание этого распре­деления равно 10. Нормированная статистика критерия 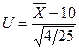имеет нормальное распределение N (0,1).

5) альтернативная гипотеза Н ₁: т < 10предполагает уменьшение расхода топлива, следовательно, нужно использовать односторонний критерий. Критическая область определяется не­равенством U <и_а. По таблице приложений П1 находим u_0,05=-u_0,95=-1,645;

6) выборочное значение нормированной статистики критерия равно .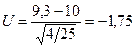

7) статистическое решение: так как выборочное значение статистки критерия принадлежит критической области, гипотеза Н₀ отклоняется: следует считать, что изменение конструкции
двигателя привело к уменьшению расхода топлива.

Граница 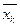критической области для исходной статистики X критерия может быть получена из соотношения 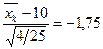, откуда получаем 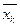= 9,342, т. е. критическая область для статистики X определяется неравенством 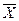< 9,342.

12.2. Ошибки первого и второго рода

Следует помнить, что статистическое решение может быть ошибочным. При этом различают ошибки первого и второго рода.

Ошибкой первого рода называют ошибку, состоящую в том, что гипотеза Н₀ отклоняется, в то время как она верна. Вероят­ность ошибки первого рода равна вероятности попадания статистики критерия в критическую область при условии, что верна гипотеза Н₀, т. е. равна уровню значимости α: P[Z Î V_K/ Н₀ ]= α.

В рассмотренном выше примере 50 вероятность ошибки первого рода равна 0,05.

Ошибка второго рода происходит в том случае, если гипо­теза Н ₀ принимается, но в действительности верна альтернатив­ная гипотеза Н ₁. Вероятность ошибки второго рода β можно вы­числить (при простой альтернативной гипотезе Н ₁) по формуле β = P[ZÎV\V_K/ H ₁].

Пример 51. В условиях примера 50 предполагаем, что на­ряду с гипотезой Н ₀: т = 10 л рассматривается альтернативная гипотеза Н ₁: т = 9л. В качестве статистики критерия снова возь­мем выборочное среднее 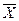. Предположим, что критическая об­ласть задана следующим неравенством 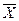< 9,44 л. Найти вероят­ности ошибок первого и второго рода для критерия с такой кри­тической областью.

Решение. Найдем вероятность ошибки первого рода. Стати­стика 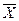критерия при условии, что верна гипотеза Н ₀: т = 10, имеет нормальное распределение 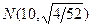. Используя табли­цу приложений (П1), находим

.

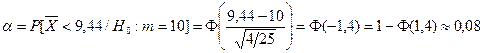Полученный результат означает, что принятый критерий классифицирует ~8% автомобилей, имеющих расход 10 л на 100 км пробега, как автомобили, имеющие меньший расход топлива.

При условии, что верна гипотеза Н ₁: т = 9, статистика X имеет нормальное распределение 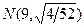. Вероятность ошибки второго рода в этом случае равна

.

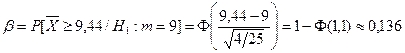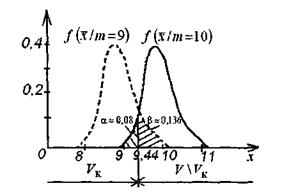
Рис. 16.

Итак, в соответствии с принятым критерием 13,6% автомобилей, имеющих расход топлива 9 л на 100 км пробега, классифицируются как автомобили, имеющие расход 10 л. Вероятности ошибок первого и второго рода показаны в виде заштрихованных площадей под кри­выми плотностей распределения статистики критерия на рис. 16.

При заданной вероятности α ошибки первого рода вероят­ность ошибки второго рода может быть уменьшена путем увели­чения объема выборки. Если при этом вероятность ошибки второ­го рода не должна превышать заданного значения β, то мини­мальный объем выборки п можно найти из решения системы P[z<=V_K/H₀] = α, P=P[ZÎV\V_K/ Н ₁ ]≤β.

Аналитическое решение такой системы возможно в про­стейших случаях.

Пример 52. Какой минимальный объем выборки п следует взять в условиях примера 50, чтобы при проверке гипотезы Н ₀: т = 10 л против альтернативной гипотезы Н ₁: т = 9 л ошиб­ка первого рода была равна α = 0,01, а ошибка второго рода не превышала 0,1? Какова критическая область в этом случае?

Решение. Так как в альтернативной гипотезе Н ₁ предпола­гается меньшее значение параметра т, то критическая область V_K определяется неравенством 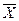< 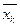. По условию задачи имеем

,

.

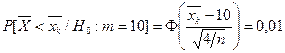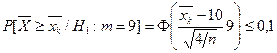Запишем систему следующим образом:

,

.

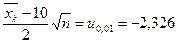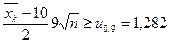Исключая 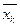, получим, что n ≥ 53. Подставляя наименьшее значение п в первое уравнение системы, найдем границу критиче­ской области: .

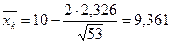Следовательно, критическая область V_K определяется нера­венством 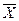< 9,361.

Проверка статистических гипотез с использованием крите­риев значимости может быть проведена на основе доверительных интервалов. При этом одностороннему критерию значимости со­ответствует односторонний доверительный интервал, а двусто­роннему критерию значимости - двусторонний доверительный интервал. Гипотеза Н ₀ принимается, если значение θ₀ накрыва­ется соответствующим доверительным интервалом; в противном случае гипотеза Н ₀ отклоняется.

Если проверяется гипотеза Н₀: θ₁= θ₂, то рассматривается доверительный интервал для разности θ₁- θ₂. Гипотеза Н₀ при­нимается, если доверительный интервал для разности параметров θ₁- θ₂ накрывает нулевое значение. Исключение составляет про­верка гипотезы о равенстве дисперсий Н₀: 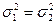так как дове­рительный интервал строится для отношения дисперсий, то гипо­теза Н₀ в этом случае принимается, если доверительный интервал накрывает значение, равное единице.

Пример 53. В условиях примера 50 проверить гипотезу Н₀: т = 10 л при альтернативной гипотезе Н ₁: т < 10 л на уровне значимости α = 0,05, используя доверительный интервал для па­раметра т.

Решение. Найдем границу т₂ левостороннего доверитель­ного интервала (-∞, т₂) для параметра т при доверительной ве­роятности 1- α = 0,95. Используя выборочное среднее = 9,3 и начение квантили u _0,95 = 1,645, получим

.

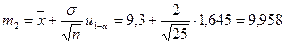Так как значение т = 10 не накрывается интервалом (-∞;9,958), то гипотезу Н₀ следует отклонить, что совпадает с результатом, полученным при решении примера 50.

12.3. Критерии значимости для проверки гипотез

Таблица 6

Дата добавления: 2014-11-20