Вариационная постановка начально-краевой задачи. Функционал начально-краевой задачи для гиперболического уравнения имеет вид

Функционал начально-краевой задачи для гиперболического уравнения имеет вид

,

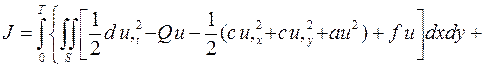
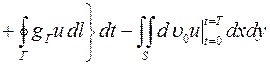где функции Q = Q (x, y, t), g_Г = g_Г (x, y, t) и u ₀(x, y) считаются известными и поэтому не варьируются. Вариация рассматриваемого функционала будет иметь вид

.

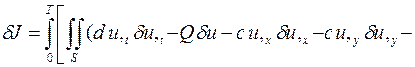
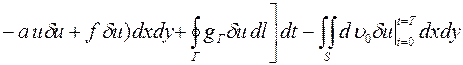Применение к первому слагаемому подынтегрального выражения интегрирования «по частям» по времени t, а к третьему и четвёртому слагаемым – интегрирования по x и y с представлением Q и g_Г в следующем виде

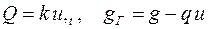
позволяют записать вариацию функционала в виде

.

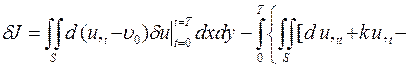
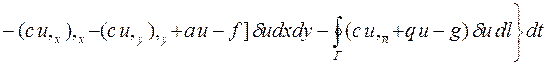Использование необходимого условия существования экстремума рассматриваемого функционала

позволяет получить гиперболическое уравнение

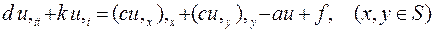
его возможные варианты граничных условий на контуре области S

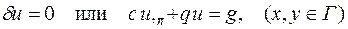
и его граничные условия по времени t

.

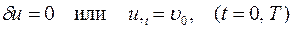Возможные варианты граничных условий при t =0 и t = T преобразуются к двум начальным условиям при t = 0

.

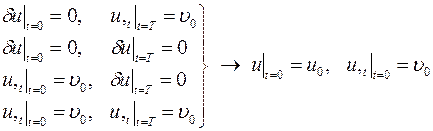Алгоритм метода конечных элементов

В соответствии с алгоритмом метода конечных элементов область поиска решения в пространстве { x, y } разбивается на треугольные элементы, для каждого из которых вводится своя локальная система координат ξ 0 η. Внутри каждого элемента искомое решение гиперболического уравнения представляется билинейной функцией

,

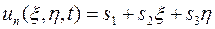где коэффициенты s ₁, s ₂ и s ₃ являются функциями времени t. В матричной форме с заменой коэффициентов s ₁, s ₂ и s ₃ значениями искомого решения 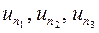в узлах конечного элемента такое представление решения имеет вид

.

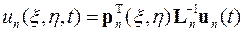Здесь

, , .

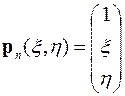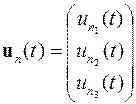Аналогично представляются коэффициенты и функции гиперболического уравнения и его граничных и начальных условий в пределах каждого элемента

,

,

,

,

.

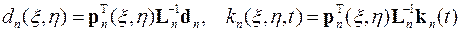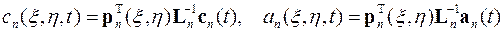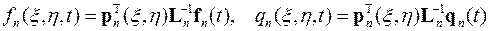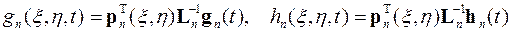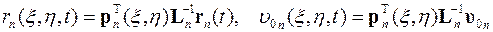Затем для каждого конечного элемента записывается функционал, эквивалентный рассматриваемой начально-краевой задаче

.

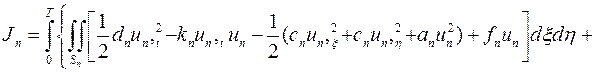
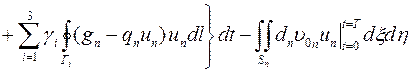После подстановки в это выражение представления искомого решения и коэффициентов, и выполнение операций интегрирования по площади и по контуру конечного элемента функционал записывается в виде

,

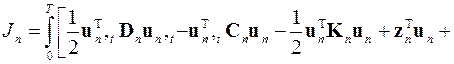
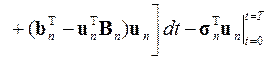где

,

,

,

,

,

,

,

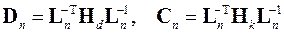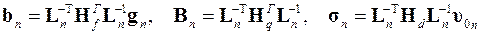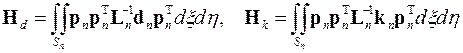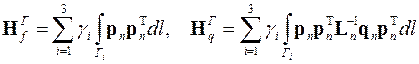Здесь D _n, С _n, K _n и B _n – квадратные симметричные матрицы (3×3 элем.), последние две из которых принято называть матрицами жёсткости элемента и его границы, а z _n, s _n и b _n – векторы внешнего воздействия (по 3 элем.) на конечный элемент.

Следующий шаг алгоритма метода конечных элементов предполагает «сборку» конечно-элементной схемы, которая имеет целью получение функционала задачи для всей области поиска решения. Для этого функционалы для каждого элемента сначала суммируются

,

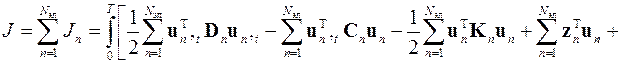
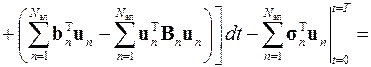
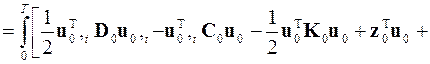
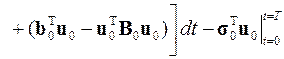где D ₀, С ₀, K ₀ и B ₀ – объединённые матрицы, аналогичные ранее введённым матрицам D _n, С _n, K _n и B _n, z ₀, s ₀ и b ₀ – объединённые векторы внешнего воздействия на элементы, а u ₀ – объединённый вектор решения в узлах конечных элементов

,

,

.

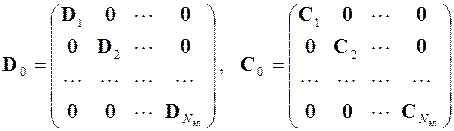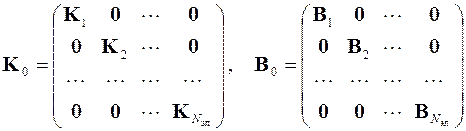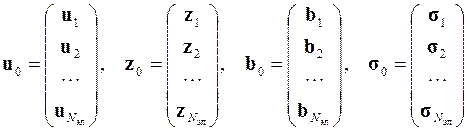После этого для описания способа объединения конечных элементов в область поиска решения S формируется матрица геометрии Г, которая связывает объединённый вектор решения u ₀ с вектором u обобщённого решения в узлах самой области S

,

где

.

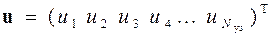В итоге функционал начально-краевой задачи для всей области S поиска решения будет иметь вид

,

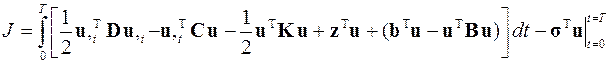где D = Г ^Т D ₀ Г, С = Г ^Т С ₀ Г, K = Г ^Т K ₀ Г и B = Г ^Т B ₀ Г – матрицы для всей области S поиска решения и её границы Г, аналогичные ранее введённым матрицам D _n, С _n, K _n и B _n, а z = Г ^Т z ₀, s = Г ^Т s ₀ и b = Г ^Т b ₀ – векторы внешнего воздействия.

Для получения конечно-элементных уравнений рассматриваемой начально-краевой задачи необходимо выполнить интегрирование первого подынтегрального слагаемого «по-частям» по времени

,

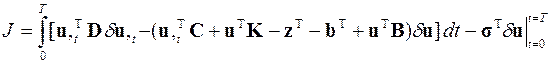и потребовать минимума её функционала в виде необходимого условия его экстремума

.

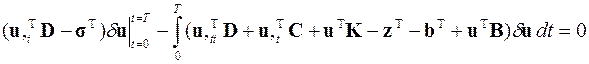Результатом этих действий с учётом того, что вариация δ u не может быть тождественно равной нулю, является матричное уравнение, показывающее изменение искомого решения по времени, и соответствующие ему начальные условия

,

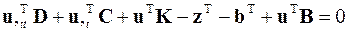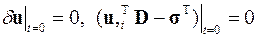
или

, ,

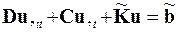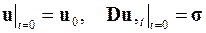где

.

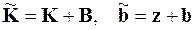Полученное матричное уравнение, как и в случае с параболическим уравнением, представляет собой систему обыкновенных линейных дифференциальных уравнений относительно значений решений в узлах конечно-элементной сетки – u_i 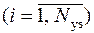. Методы решения такой задачи известны по разделу «Решение задачи Коши для нормальных систем обыкновенных дифференциальных и уравнений высших порядков» [3]. Однако перед решением полученную задачу Коши надо преобразовать с учётом граничных условий 1-го типа, поскольку граничные условия 2-го типа в методе конечных элементов выполняются автоматически.

Если в какой-либо узловой точке с номером n на границе Г задано граничное условие 1-го рода

,

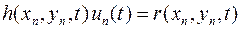то коэффициенты матриц D, С и 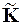и вектора 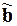соответствующие узловому значению решения u_n преобразуются следующим способом: диагональные элементы n -х строк матриц D и С заменяются единицами, а все остальные элементы этих строк и соответствующих столбцов обнуляются. В n -ой строке и в n -м столбце матрицы 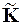обнуляются все элементы, а n -й элемент вектора 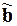заменяется выражением

.

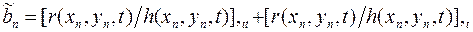Оценка погрешности решения

Оценка погрешности конечно-элементного решения начально-краевой задачи для гиперболического уравнения выполняется так же, как для параболического уравнения.

Если интервальная оценка погрешности численного решения задачи Коши на отрезке [0, t ] пренебрежимо мала по сравнению с получаемой величиной погрешности конечно-элементного решения, то последняя оценивается по правилу Рунге

,

,

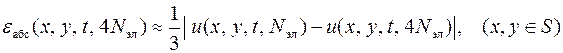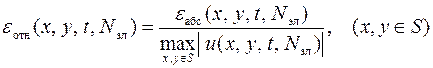где 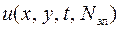и 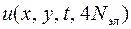– два решения рассматриваемой начально-краевой задачи с размерами конечных элементов, отличающихся в два раза.

Дата добавления: 2014-12-16