
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Квадратурні формули з рівновіддаленими вузлами: формула трапецій
|
|
|
|
Отрезок интегрирования [a,b] разбивается на n равных интервалов длиной 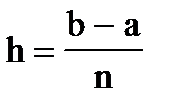 . В пределах каждого интервала [xi,xi+1] функция f(x) заменяется интерполяционным многочленом Лагранжа первой степени с узлами xi,xi+1, т.е. прямой линией. Значение интеграла в пределах [xi,xi+1] заменяется площадью трапеции:
. В пределах каждого интервала [xi,xi+1] функция f(x) заменяется интерполяционным многочленом Лагранжа первой степени с узлами xi,xi+1, т.е. прямой линией. Значение интеграла в пределах [xi,xi+1] заменяется площадью трапеции:
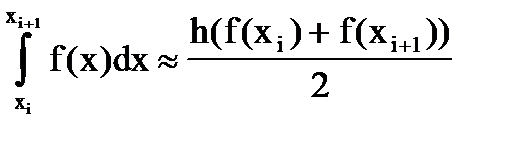 .
.
Суммирование значений интеграла по всем n участкам разбиения дает общую площадь, т.е. приближенное значение интеграла:
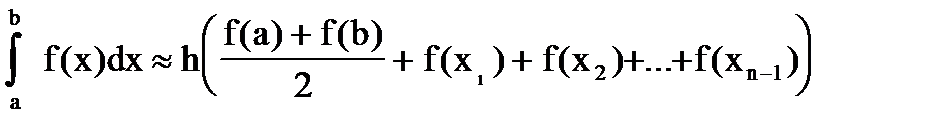 .
.
Если функция f(x) имеет на отрезке [a,b] непрерывную вторую производную, то оценка погрешности усечения может быть осуществлена по формуле:
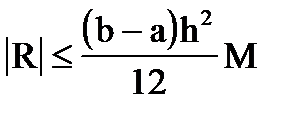 ,
,
где 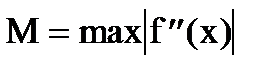 , a£x£b.
, a£x£b.
19. Квадратурні формули з рівновіддаленими вузлами: формула парабол(Сімпсона)
Формула Симпсона получается из квадратурных формул Ньютона - Котеса при n=2, т.е. интерполяционный многочлен, которым заменяют подынтегральную функцию, многочлен второго порядка. При n=2 получаем
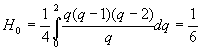 ,
, 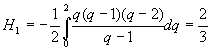 ,
, 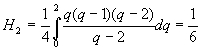 ,
,
получаем формулу Cимпсона
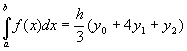 .
.
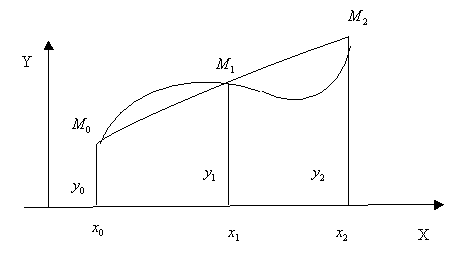
Формула носит название формулы Симпсона. Геометрически эта формула получается в результате замены кривой 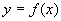 параболой
параболой 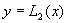 , проходящей через точки:
, проходящей через точки: 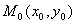 ,
, 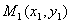 ,
, 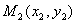 .
.
Погрешность формулы Симпсона равна
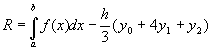 .
.
Применяя простую теорему о среднем для функции 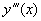
на [a,b] получаем: 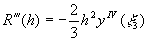 , где
, где 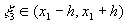 . Кроме того, имеем:
. Кроме того, имеем: 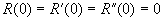 . Последовательно интегрируя
. Последовательно интегрируя 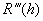 и используя интегральную теорему о среднем, находим:
и используя интегральную теорему о среднем, находим:
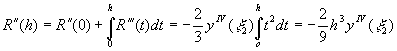 .
.
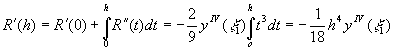 .
.
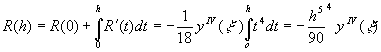 .
.
где 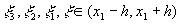 . Таким образом, окончательно имеем
. Таким образом, окончательно имеем
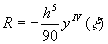 .
.
Из формулы видно, что она является точной для многочленов не только второй, но и третьей степени, т.е. формула Симпсона при относительно малом числе ординат обладает повышенной точностью.
Формула Симпсона также может быть применена не сразу ко всему отрезку, а к отдельным частям его. Если разобьем [a,b] на 2m равных частей шагом 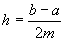 , то получим:
, то получим:
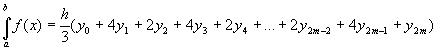 .
.
|
|
|
Формула называется обобщённой формулой Симпсона. Введём обозначения:
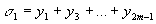 ,
, 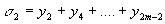 .
.
Обобщённая формула Симпсона может быть записана в новых обозначениях так:
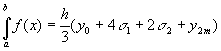 .
.
|
|
|
|
|
Дата добавления: 2015-01-03; Просмотров: 486; Нарушение авторских прав?; Мы поможем в написании вашей работы!