Линейная непрерывная детерминированная модель многомерной динамической системы в переменных состояния

Представление в переменных состояния основано на использовании теоремы Коши об эквивалентности представления обыкновенного дифференциального уравнения (ДУ) n -го порядка в виде системы n уравнений 1-го порядка.

Рассмотрим в качестве примера переход от описания модели в виде линейного дифференциального стационарного уравнения 2-го порядка к описанию модели в виде системы двух уравнений 1-го порядка, а затем – к стандартной модели в виде переменных состояния.

Пример. Пусть некая динамическая система описывается линейным ДУ 2-го порядка с постоянными коэффициентами:

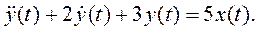
Обозначим:

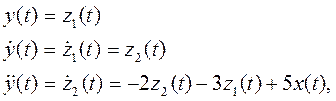
и тогда можно выразить исходное уравнение в виде двух уравнений через состояния z₁(t) и z₂(t).

Запишем полученную систему из 2-х уравнений 1-го порядка в так называемом векторно-матричном виде:

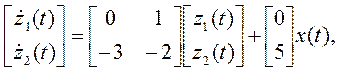
где z (t) – вектор состояния; x (t) – вектор управления (в данном примере, в частности, x(t) – скаляр).

Это удобная форма записи, т.е. удобная модель динамической системы, использующая понятие переменных состояния z_i(t). Такая модель позволяет проследить изменение во времени каждой из составляющих внутренних переменных системы и вывести условия ее управляемости и наблюдаемости (п. 2.7).

Состояние системы отделяет будущее от прошлого, содержит всю информацию о прошлом системы, необходимую для определения реакции на произвольный входной сигнал.

В общем случае n -го порядка исходного линейного ДУ можно записать векторно-матричное уравнение состояния системы

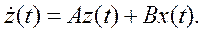
Здесь матрица А (n × n) называется матрицей объекта, а матрица В (n × m), где m – размерность вектора управления – матрицей управления. Такая форма уравнений, разрешенных относительно первых производных, называется стандартной формой.

Не всегда оказывается возможным измерить все состояния системы: z₁, z₂, …, z_n, поэтому вводится уравнение наблюдения, которое позволяет описать, какие из состояний z_i и какие из входов x_i попадают в вектор наблюдаемых выходных переменных y (t):

,

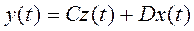где z (t) – вектор состояния системы; x (t) – вектор управления; С ­–

матрица наблюдения.

Уравнение наблюдения также является линейным, причем не дифференциальным, а алгебраическим.

В рассмотренном примере 2.4.1 матрица объекта А равна:

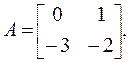
ее размерность равна (2 × 2).

Матрица управления В представляет собой вектор-столбец (2 × 1), поскольку вектор управления x(t) в этом примере – скаляр (1 × 1):

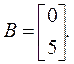
Матрица наблюдения С равна единичной матрице:

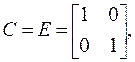
а матрица D – нулевой:

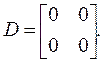
Уравнения состояния и наблюдения соответствуют структурной схеме (рис. 2.10), где матрицы A, B, C и D указаны как стационарные (с постоянными элементами), хотя в случае нестационарных линейных систем схема останется такой же. Знак ∫ обозначает на схеме блок интегрирования: действительно, на входе этого блока находится производная вектора состояния, а на выходе – сам вектор состояния z (t).

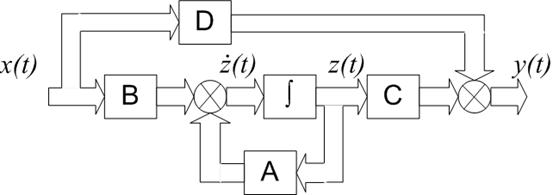
Рис. 2.10. Структурная схема модели линейной стационарной системы управления в переменных состояния

Очевидно, что использование модели переменных состояния для анализа многомерных систем требует привлечения теории матриц и линейных векторных пространств.

Более подробный материал по теории матриц можно найти в Приложении 1 в конце данного пособия.

Вопросы к разделу 2.4

1. Какую информацию содержит вектор состояния системы?
2. Какая теорема позволяет перейти от линейного дифференциального уравнения n -го порядка к векторно-матричному уравнению состояния?
3. Что описывает уравнение состояния?
4. Что описывает уравнение наблюдения?
5. Какова размерность матрицы объекта?
6. Какова размерность матрицы управления?

Дата добавления: 2014-12-27