Пример 2-4 Комбинированные преобразования на плоскости

.

Пример 2-3 Отражение и вращение

Рассмотрим треугольник ABC, показанный на рис. 2-7. Первоначально

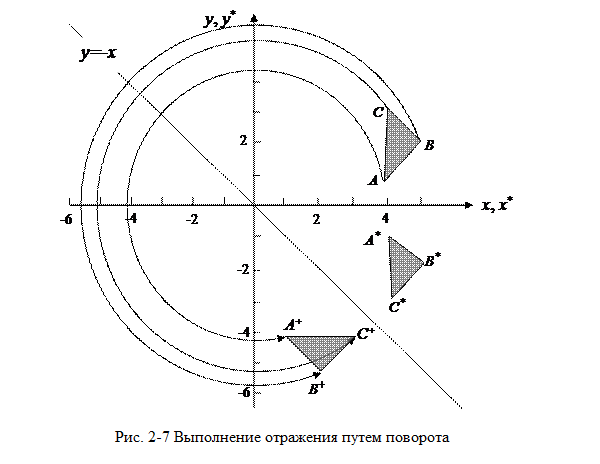
отобразим его относительно оси х (уравнение 2-33), а затем относительно прямой у =- х (см. выражение (2-36)). Результатом первого отображения будет

Результатом второго будет

Повернем треугольник относительно начала координат на угол q = 270° (см. (2-29)) и получим аналогичный результат

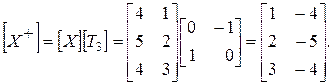
Отметим, что матрицы отражения из (2-33) и (2-36) ортогональны, т. е. транспонированная матрица одновременно является обратной. Например,

.

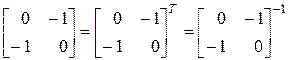2-11 МАСШТАБИРОВАНИЕ

Из наших рассуждений относительно преобразования точек следует, что величина масштабирования определяется значением элементов исходной диагональной матрицы. Если матрица

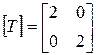
используется в качестве оператора воздействия на вершины треугольника, то имеет место «двукратное» расширение или равномерное масштабирование относительно точки начала координат. Если значения элементов не равны, то треугольник искажается, что проиллюстрировано на рис. 2-8. Треугольник ABC, преобразованный с помощью последней матрицы переходит в пропорционально увеличенный треугольник А В С . Тот же треугольник, но преобразованный с помощью матрицы

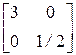
переходит в треугольник D E F , имеющий искажение, вызванное разными коэффициентами масштабирования.

В общем случае при матрице

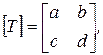(2-37)

в которой а = d, b = с = 0, выполняется пропорциональное масштабирование; если 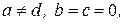то масштабирование будет проведено непропорционально. В первом случае для а = d > 1 происходит расширение, т. е. увеличение изображения.Если а = d < 1, то происходит равномерное сжатие, т.е. фигура уменьшается. Непропорциональное расширение и сжатие возникают в зависимости от значений a и d, которые могут быть меньше либо больше, чем 1, независимо друг от друга.

Из рис. 2-8 видно также, что на первый взгляд преобразование треугольника является перемещением. Это объясняется тем, что относительно начала координат масштабируются координатные векторы, а не точки.

Для того чтобы лучше понять этот факт, рассмотрим преобразования ABC в D E F более внимательно. В частности,

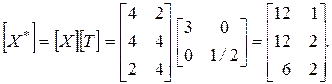
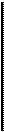Заметим, что каждая из компонент х координатных векторов треугольника ABC умножалась на масштабный коэффициент 3, а компоненты у делилась на 2.

Для того чтобы получить чистое масштабирование без эффекта перемещения, центр фигуры надо поместить в начало координат. Это видно из рис. 2-9, на котором треугольник ABC увеличивается в два раза при масштабировании относительно его центра с координатами, равными 1/3 основания и 1/3 высоты. Конкретная матрица преобразования имеет вид

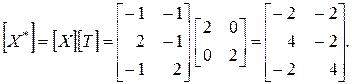
2-12 КОМБИНИРОВАННЫЕ ПРЕОБРАЗОВАНИЯ

Возможности матричного метода достаточно ясно описаны в предыдущих разделах. С помощью матричных операций над координатными векторами, определяющими вершины фигур, можно управлять формой и положением поверхности. Однако для получения желаемой ориентации может потребоваться более одного преобразования. Так как операция умножения матриц не коммутативна, то важен порядок выполнения преобразования.

Для иллюстрации эффекта некоммутативности операции умножения матриц рассмотрим преобразования поворота и отражения координатного вектора [ х у ]. Если вслед за поворотом на 90° (посредством [ T ₁]) производится отражение относительно прямой у = - x (посредством [ T ₂]), то эти два последовательных преобразования дают

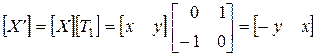
и затем

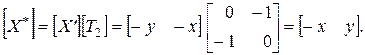
С другой стороны, если отражение следует за поворотом, то получатся следующие результаты:

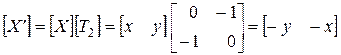
и

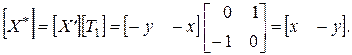
Оба результата различны, что подтверждает важность порядка применения матричных преобразований.

Другое принципиальное обстоятельство иллюстрируется этими результатамии приведенным ниже примером. Ранее отдельные матричные преобразования применялись последовательно к результатам предыдущих преобразований, например

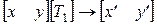
и

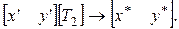
В приведенном ниже примере отдельные преобразования предварительнокомбинируются или конкатенируются, а затем полученная матрица применяется к исходному вектору, т.е. [ T ₁][ T ₂] 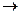[ T ₃] и [ х у ][ Т ₃] 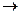[ x у ].

Рассмотрим треугольник ABC на рис. 2-10. Выполним над ним два преобра
зования: поворот на +90° вокруг точки начала координат

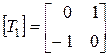
и отражение относительно линии у = - х

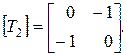
Результатом воздействия комбинированного преобразования [ Т ₃] = [ T ₁][ T ₂]

на треугольник ABC является

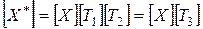
или

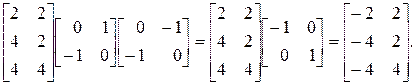
Получившийся треугольник 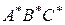является конечным результатом данного преобразования, а треугольник А'В'С' —промежуточным результатом (рис. 2-10).

Проведем преобразование в обратном порядке

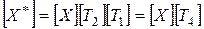
или

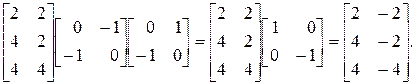
Конечным результатом будет треугольник D Е F , а промежуточным D'E'F' (рис. 2-10). Оба результата различны, тем самым снова подтверждается важность порядка применения преобразований. Отметим также, что для определителей справедливы равенства det [ Т ₃] = - 1, и det [ Т ₄]= - 1 и поэтому оба результата могут быть получены с помощью единственного отражения. Треугольник А В С можно получить из ABC путем отражения относительно оси Y (матрица [ Т ₃] и уравнение (2-34)), D E F получается из ABC при отражении относительно оси X (матрица [ Т ₄]и уравнение (2-33)).

2-13 ПРЕОБРАЗОВАНИЕ ЕДИНИЧНОГО КВАДРАТА

До сих пор мы рассматривали поведение точек и линий для определения результатов простых матричных преобразований. Однако можно корректно рассматривать применение матрицы к любой точке плоскости. Как было показано ранее, единственная точка, остающаяся инвариантной при воздействии матричных преобразований, это точка начала координат. Все другие точки плоскости подвержены преобразованию, которое можно представить как растяжение исходной плоскости, системы координат и перевод в новую форму. Формально принято считать, что преобразование вызывает переход от одного координатного пространства к другому.

Рассмотрим координатную сетку, состоящую из единичных квадратов на координатной плоскости ху (рис. 2-11). Четыре координатных вектора вершин единичного квадрата, проходящие под одним углом к началу координат, имеют следующий вид:

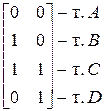
Такой единичный квадрат изображен на рис. 2-11а. Применяя к нему (2 х 2)-матрицу общего преобразования, получаем

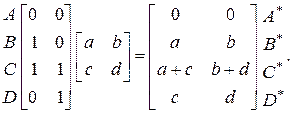(2-38)

Результаты этого преобразования показаны на рис. 2-11 b. Из выражения (2-38) следует, что начало координат не подвергается преобразованию, т.е. [ А ]= [ А ]= [0 0]. Далее отметим, что координаты В равны первой строке матрицы преобразования, а координаты D —второй. Таким образом, матрица преобразования является определенной, если определены координаты В и D (преобразование единичных векторов [1 0], [0 1]). Поскольку стороны единичного квадрата первоначально параллельны и ранее было показано, что параллельные линии преобразуются снова в параллельные, то результирующая фигура является параллелограммом.

Влияние элементов а, b, с и d матрицы 2x2 может быть установлено отдельно. Элементы b и c, как видно из рис. 2-11 b, вызывают сдвиг (см. разд. 2-4) исходного квадрата в направлениях у и х соответственно. Как отмечалось ранее, элементы a и d играют роль масштабных множителей. Таким образом, 2 х 2-матрица задает комбинацию сдвига и масштабирования.

Несложно определить также площадь параллелограмма A B C D из рис. 2-11 b, которую можно вычислить следующим образом:

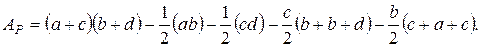
В результатеполучаем

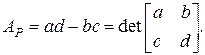(2-39)

Можно показать, что площадь любого параллелограмма A_P образованногопутем преобразования квадрата, есть функцияот определителя матрицы преобразования и связана с площадью исходного квадрата A _S простым отношением

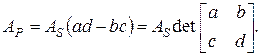(2-40)

Фактически, так как площадь всей фигуры равна сумме площадей единичныхквадратов, то площадь любой преобразованной фигуры A_t зависит от площади исходной фигуры A_i

(2-41)

Это полезный способ определения площадей произвольных фигур.

Дата добавления: 2015-04-25