Теория игр

Транспортная задача

Важным частным случаем задачи линейного программирования является транспортная задача.

Пример решения задачи.

Построить экономико-математическую модель следующей задачи. Имеются 3 поставщика и 4 потребителя. Мощность поставщиков и спросы потребителей, а также затраты на перевозку единицы груза для каждой пары «поставщик – потребитель» сведены в таблицу поставок. В каждой клетке стоит коэффициент затрат – затраты на перевозку единицы груза от соответствующего поставщика к соответствующему потребителю.

Задача. Найти объем перевозок для каждой пары «поставщик – потребитель» так, чтобы:

1) мощность всех поставщиков были реализованы;

2) спросы всех потребителей удовлетворены;

3) суммарные затраты на перевозку были минимальными.

Таблица 1.11

Транспортная задача

Поставщики	Мощность поставщиков	Потребители и их спрос
		х11	х12	х13	х14
		х21	х22	х23	х24
		х31	х32	х33	х34

Составим экономико-математическую модель задачи.

Искомый объем перевозки от i-го поставщика к j-му потребителю обозначим х_ij и назовем его поставкой. Тогда целевая функция, значение которой необходимо минимизировать, запишется в виде:

f(х) = 1x₁₁+2x₁₂+5x₁₃+…+7x₃₃+4x₃₄ → min

Система ограничений будет иметь следующий вид:

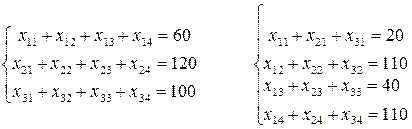
Особенности экономико-математической модели транспортной задачи:

1) Система ограничений есть система уравнений, то есть транспортная задача задана в канонической форме.

2) Коэффициенты при переменных системы ограничений равны 1 или 0.

3) Каждая переменная входит в систему ограничений 2 раза.

Решение задачи.

Существует два метода нахождения первоначального распределения поставок (опорного плана).

1) Метод северо-западного угла.

Задаем северо-западной клетке (а именно х₁₁) максимально возможную поставку (20), после этого спрос 1-го потребителя будет полностью удовлетворен, в результате чего первый столбец поставок полностью выпадает из следующего рассмотрения. В оставшейся таблице опять выбираем северо-западную клетку.

Таблица 1.12

Первый план перевозок,

построенный методом северо-западного угла

Недостаток этого метода: план строится без учета стоимости (затраты на перевозку).

2) Метод минимальной стоимости (или метод наименьших затрат).

Находим клетку с наименьшим коэффициентом затрат (у нас их две, равные 1) и даем ей максимальную поставку (так как любая из них может поставить 20, выбираем любую). Таким образом, спрос 1-го потребителя удовлетворен и его (1-й столбец) вычеркиваем. В оставшейся таблице опять ищем клетку с минимальной стоимостью.

Таблица 1.13

Первый план перевозок,

построенный методом минимальной стоимости

Ø Важно помнить. Обязательно вычеркивается только один: или поставщик, или потребитель. Если на очередном шаге решения задачи совпали потребность покупателя и мощность поставщика, то одного (любого) вычеркиваем, а у второго пишем в остатке 0. На следующем шаге решения перевозим 0, тогда эта клетка участвует в плане перевозок. Если этого не сделать, то в плане будет недостаточно клеток, чтобы заполнить таблицу потенциалов.

Вычислим для обоих опорных планов суммарные затраты на перевозку.

S₁ = 20*1 + 40*2 + 70*6 + 40*5 + 10*2 + 100*4 = 1140

S₂ = 60*2 + 20*1 + 100*2 + 50*3 + 40*7 + 10*4 = 810

Во втором случае по числу шагов мы находимся ближе к оптимуму.

Решение методом потенциалов.

Выпишем отдельно полученный план перевозок X[1]

Таблица 1.14

Первый план перевозок

	60 –	+
	50 +	40 –

Вычисляем его стоимость: S(X[1])=60*2 + 100*1 + 20*2 + 50*3 + + 40*7 + 10*4 = 810.

Таблица 1.15

Потенциалы и косвенные стоимости

β α
	2^’ -1		6^’ -1	3^’ 0
		1^’ 5	5^’ 0
	3^’ 3

а) Вписываем в таблицу стоимости перевозок, соответствующих опорному плану.

б) Задаем произвольно один из потенциалов и вычисляем остальные, учитывая, что сумма потенциалов равна стоимости перевозки (в данной задаче задали ).

в) Вычисляем косвенные стоимости (суммируем соответствующие потенциалы и заполняем свободные клетки таблицы), помечаем косвенные стоимости штрихом.

г) Находим разницу между стоимостью, заданной в задаче, и косвенной стоимостью (цифры справа в клетке).

д) Выберем максимальную отрицательную разность и введем ее в опорный план, то есть увеличивая ее значение на какую-то величину, тогда значение другой переменной должно уменьшиться на эту же величину и так далее, замыкаем цикл. (Этот процесс называется цикл пересчета).

е) Если отрицательных значений нет, значит найденный опорный план является оптимальным.

ж) Определяем максимальную величину, на которую может быть увеличена клетка, вводимая в опорный план, так чтобы количество перевозки не стало отрицательным (в нашем случае она может быть равной 40).

Получаем новый опорный план: X[2].

Таблица 1.16

Второй, улучшенный план перевозок

+	20 –
20 –			100 +
	90 +		10 –

Его стоимость S(X[2])= 810 – 40*1 = 770 меньше предыдущего значения, значит полученный план ближе к оптимальному. Вычислим потенциалы для найденного опорного плана, положив , косвенные стоимости и разницу между заданными и косвенными стоимостями.

Таблица 1.17

Потенциалы и косвенные стоимости для второго плана перевозок

β α	-3	-3		-2
	2^’ -1			3^’ 0
		1^’ 5	4^’ 1
	3^’ 3		6^’ 1

Единственная клетка с отрицательной разностью, это клетка (1, 1). Следовательно, эту клетку можно ввести в опорный план. Максимальная величина, на которую может увеличиться клетка, чтобы опорный план не стал отрицательным 10 (эту величину выбираем из клеток, помеченных знаком «–»). Перевозка (3, 5) выйдет из опорного плана. Остальные перевозки изменятся соответственно знакам: прибавляем 10 к перевозкам, помеченным знаком «+», и вычитаем из перевозок, помеченных знаком «–».

Ø Важно помнить. На каждом шаге решения задачи одна перевозка входит в опорный план и одна выходит из него. Количество клеток, участвующих в плане перевозок, в ходе решения задачи не меняется. Если получается две клетки с одинаковыми минимальными значениями, помеченными знаком «–», то одна выходит из опорного плана, а во второй (в любой) остается 0, то есть клетка участвует в плане перевозок.

Получили план X[3].

Таблица 1.18

Третий план перевозок

Его стоимость S(X[3]) = 770 – 10*1 = 760, то есть стала еще меньше.

Чтобы выяснить, является ли полученный план оптимальным, вычислим потенциалы и косвенные стоимости для полученного плана.

Таблица 1.19

Потенциалы и косвенные стоимости для третьего плана перевозок

β α	-4	-3		-2
				3^’ 0
		2^’ 4	5^’ 0
	2^’ 4		6^’ 1	4^’ 0

Все разности между заданными и косвенными стоимостями положительны, следовательно оптимальный план перевозок X 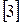найден и стоимость его равна 760 денежным единицам.

Ø Важно помнить. Описанный метод потенциалов позволяет решать только сбалансированные задачи, то есть задачи, в которых суммарная мощность поставщиков равна суммарному спросу потребителей.

На практике такая ситуация встречается редко, поэтому любую транспортную задачу можно привести к сбалансированной.

Если в транспортной задаче суммарная мощность поставщиков меньше суммарного спроса потребителей, то такая задача называется задачей на недостаток. Для ее решения необходимо ввести фиктивного поставщика, стоимости перевозок которого будут равны нулю, а мощность равна разности суммарного спроса потребителей и суммарной мощности действительных поставщиков, то есть размеру недостатка.

Если в транспортной задаче суммарный спрос потребителей меньше суммарной мощности поставщиков, то такая задача называется задачей на избыток. Для ее решения необходимо ввести фиктивного потребителя, стоимости перевозок которого будут равны нулю, а мощность равна разности суммарной мощности поставщиков и суммарного спроса действительных потребителей, то есть размеру избытка.

Когда задача решена, цифры в строке фиктивного поставщика показывают, какое количество продукции, кто из потребителей не получит, так как задача была на недостаток.

Когда задача решена, цифры в строке фиктивного потребителя показывают, какое количество продукции, у кого из поставщиков останется, так как задача была на избыток.

Задания для самостоятельной работы.

1. Решить транспортную задачу.

Таблица 1.20

Данные о стоимости перевозок,

мощностях поставщиков и спросе потребителей

2. Составить экономико-математическую модель задачи, найти оптимальное распределение поставок и минимальные затраты на перевозку.

Таблица 1.21

Данные о стоимости перевозок,

мощностях поставщиков и спросе потребителей

Поставщики	Мощность поставщиков	Потребители и их спрос

Что означают следующие термины и понятия?

Целевая функция	Ведущий элемент
Допустимое множество	Двойственная задача
Оптимальное решение	Оценки ресурсов
Система ограничений	Функция Лагранжа
Тривиальные ограничения	Множители Лагранжа
Задача линейного программирования	Условия дополняющей нежесткости
Допустимое решение	Транспортная задача
Каноническая форма задачи	Метод потенциалов
Стандартная форма задачи	Цикл пересчета
Опорный план	Косвенные стоимости
Базисные переменные	Задача на избыток
Свободные переменные	Задача на недостаток
Ведущая строка	Поставка
Ведущий столбец	Метод минимальной стоимости

Теперь вы должны уметь:

o составлять экономико-математические модели экономических задач;

o решать задачи линейного программирования графическим методом;

o решать задачи линейного программирования симплексным методом;

o решать задачи математического программирования методом Лагранжа;

o решать транспортные задачи;

o приводить любые транспортные задачи к сбалансированным;

o объяснять экономический смысл функции и ограничений в экономико-математических моделях задач;

o провести анализ использования ресурсов предприятия, используя теорию двойственности;

o приводить задачи к каноническому виду из стандартного и наоборот;

o анализировать результаты решения задач математического и линейного программирования;

o находить решение задачи, используя решение взаимно двойственной задачи.

Контрольные вопросы:

1. Какие задачи называются задачами линейного программирования?

2. Почему все переменные неотрицательные, как называются эти ограничения?

3. Какое допустимое решение называется оптимальным?

4. Чем отличаются каноническая и стандартная задачи линейного программирования?

5. Геометрическое истолкование и свойства канонической задачи линейного программирования.

6. Типы экономических задач, сводящихся к задачам линейного программирования.

7. При решении задачи симплексным методом какой столбец называется ведущим, какая строка ведущей и какой элемент ведущим?

8. Какой экономический смысл коэффициентов столбца Q? Почему при заполнении столбца Q делим только на положительные коэффициенты ведущего столбца?

9. Почему решение считается найденным, если коэффициенты последней строки таблицы положительные?

10. Какой экономический смысл имеют коэффициенты столбца свободных членов последней таблицы?

11. Экономическая интерпретация двойственной задачи.

12. Свойства взаимно двойственных задач.

13. Экономический смысл транспортной задачи?

14. Когда транспортная задача является задачей на избыток, а когда задачей на недостаток, как это исправить?

15. В чем суть метода северо-западного угла?

16. В чем суть метода минимальной стоимости?

17. Когда опорный план считается оптимальным, то есть решение найдено?

18. Какие типы экономических задач сводятся к транспортной задаче?

19. Что показывают цифры в строке фиктивного поставщика и в столбце фиктивного потребителя, когда транспортная задача решена?

Одним из важных разделов «Исследования операций» является теория игр, представляющая собой теоретические основы математических моделей принятия оптимальных решений в конфликтных ситуациях рыночных отношений, носящих характер конкурентной борьбы, в которых одна противоборствующая сторона выигрывает за счет проигрыша другой. Наряду с такой ситуацией в теории принятия решений также рассматривают так называемые ситуацию риска и ситуацию неопределенности, которые имеют различные модели и требуют разных критериев выбора оптимальных решений. В ситуации риска предполагаются известными не только возможные условия, в которых нужно принимать решение, но и вероятности их появления. В ситуации неопределенности вероятности условий неизвестны и нет никакой возможности получить о них дополнительную статистическую информацию. Окружающая решение задачи среда, которая проявляется в тех или иных условиях, называется природой, а соответствующие математические модели называются играми с природой или теорией статистических решений.

Теория игр была систематически изложена ДЖ. Фон Нейманом и О. Монгерштерном в 1944 году. Они написали книгу, которая содержала главным образом экономические примеры, поскольку экономическому конфликту легче придать численную форму. Теория игр используется в области экономики и производства, бизнеса и финансов, сельского хозяйства и военного дела, биологии и социологии, психологии и политологии. К настоящему времени теория игр развилась в самостоятельную область математики и может рассматриваться независимо от ее приложений к реальным игровым ситуациям. По мнению лауреата Нобелевской премии по экономике за 1994 г. Нэша, теория игр вообще сыграла важную роль в интеллектуальной жизни ХХ века.

На практике часто приходится сталкиваться с задачами, в которых необходимо принимать решения в условиях неопределенности, то есть возникают ситуации, в которых две (или более) стороны преследуют различные цели, а результаты любого действия каждой из сторон зависят от мероприятий партнера. Такие ситуации, возникающие при игре в шахматы, шашки, домино, ситуации на рынке, когда выходит несколько производителей с одинаковым товаром (олигополия), покупатель и продавец, поставщик и потребитель, банк и клиент. То есть примером теории игр являются такие ситуации, в которых важную роль играют конфликты и совместные действия. Конфликт может возникнуть также из различия целей, которые отражают не только несовпадающие интересы различных сторон, но и многосторонние интересы одного и того же лица, например разработчик экономической политики обычно преследует разнообразные цели (рост объема производства, повышение доходов, снижение экологической нагрузки).

Таким образом, теория игр изучает и рассматривает методы определения оптимального поведения при управлении системами, в которых характерно наличие конфликтной ситуации (столкновение интересов). Для конфликтов характерно то, что ни один из его участников заранее не знает решений, принимаемых остальными участниками. Другими словами, участники конфликтов вынуждены действовать в условиях риска и неопределенности. Неопределенность исходов может проявляться не только в результате сознательных действий других участников, но и как результат действий тех или иных стихийных сил.

В свете «теории игр» можно рассмотреть экономику, общественные науки, бизнес и повседневную жизнь. К примеру, в экономике с точки зрения «теории игр» можно объяснить торговые и ценовые войны. Кроме того, некоторые обозреватели полагают, что, используя эту теорию, можно показать причины такого феномена, как «малоподвижные» цены. В соответствии с этой теорией фирмы заключают нечто вроде тайного соглашения о преобладающем значении цены (скажем, если речь идет об автомобильной или сталелитейной промышленности). После того как они пришли к соглашению, фирмы отказываются понижать или повышать цены, так как в противном случае участники рынка будут рассматривать такие изменения как сигнал объявления экономической войны. С помощью теории игр можно также объяснить, почему иностранная конкуренция может привести к более ожесточенной ценовой войне. Что случится, если японская фирма войдет на американский рынок, на котором уже существующие компании тайно договорились назначить высокую цену? Зарубежные фирмы могут «отказаться играть в эту игру». Они просто будут снижать цены в целях овладения большей долей рынка. Сговор может разрушиться.

Для грамотного решения задач с конфликтными ситуациями необходимы научно обоснованные методы. Такие методы разработаны математической теорией конфликтных ситуаций, которые носят название «теория игр».

Всякая претендующая на адекватность математическая модель социально-экономического явления должна отражать присущие ему черты конфликта, то есть описывать:

а) множество заинтересованных сторон, которые называются игроками;

б) возможные действия каждой из сторон, именуемые стратегиями или ходами;

в) интересы сторон, представленные функциями выигрыша (платежа) для каждого из игроков.

Сама модель конфликтной ситуации называется игрой.

Дата добавления: 2015-05-09