
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Правило Лопиталя
|
|
|
|
Теорема. Пусть функции 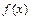 и
и 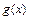 :
:
1) дифференцируемы в некоторой окрестности точки 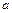 (
(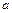 - число или
- число или 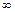 ), за исключением, может быть, самой точки
), за исключением, может быть, самой точки 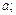 2) являются одновременно либо бесконечно малыми, либо бесконечно большими при
2) являются одновременно либо бесконечно малыми, либо бесконечно большими при 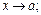 3)
3) 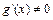 в указанной окрестности. Если существует конечный предел
в указанной окрестности. Если существует конечный предел 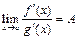 (
(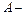 конечное либо
конечное либо 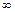 ), то существует и
), то существует и 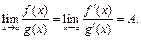
Данное утверждение справедливо и для одностороннего предела, когда 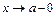 либо
либо 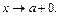
Пример 1. Найти 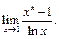
Имеем неопределённость вида 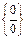 , условия теоремы выполнены. Поэтому согласно правилу Лопиталя получим:
, условия теоремы выполнены. Поэтому согласно правилу Лопиталя получим:
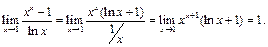
Пример 2. Найти 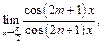
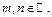
Раскроем неопределённость вида  по правилу Лопиталя:
по правилу Лопиталя:
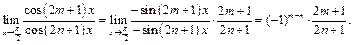
Иногда правило Лопиталя приходится применять последовательно несколько раз, чтобы избавиться от неопределённости.
Пример 3. Найти 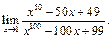
Для неопределённости 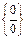 по теореме Лопиталя получим:
по теореме Лопиталя получим:
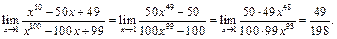
Применяя теорему Лопиталя, можно использовать известные асимптотические равенства, поскольку это иногда существенно упрощает выкладки.
Пример 4. Найти 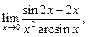
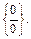
Учитывая, что при 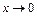
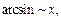 будем иметь:
будем иметь:
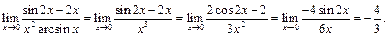
Пример 5. Найти 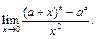
Применяя к неопределённости вида  правило Лопиталя последовательно два раза, получим:
правило Лопиталя последовательно два раза, получим:
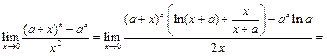
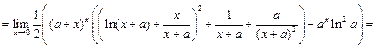
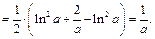
В примерах 6-9 требуется раскрыть неопределённость вида 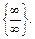
Пример 6. Найти 
Используя эквивалентность 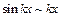 при
при 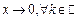 и теорему Лопиталя, получим:
и теорему Лопиталя, получим:

Пример 7. Найти 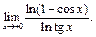
Применяя правило Лопиталя два раза, будем иметь:
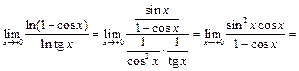
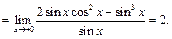
Пример 8. Найти 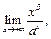
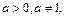
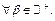
Для 
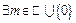 такое, что
такое, что 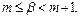 а тогда
а тогда 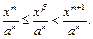 Покажем, что для
Покажем, что для 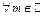
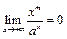 , применив правило Лопиталя
, применив правило Лопиталя 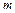 раз:
раз: 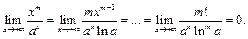
Согласно принципу двустороннего ограничения:
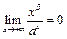 для
для 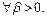
Пример 9. Найти 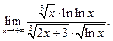
По теореме о пределе произведения получим:
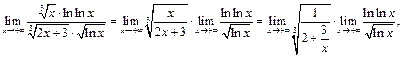 а к пределу
а к пределу  применим правило Лопиталя:
применим правило Лопиталя:
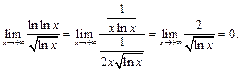
Тогда 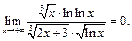
Для раскрытия неопределённости вида 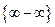 необходимо сначала преобразовать выражение, чтобы получить неопределённость
необходимо сначала преобразовать выражение, чтобы получить неопределённость  или
или 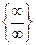 .
.
|
|
|
Пример 10. Найти 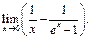
C помощью элементарных преобразований сведём неопределённость вида 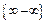 к неопределённости
к неопределённости 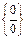 , воспользуемся асимптотическим равенством
, воспользуемся асимптотическим равенством 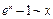 при
при 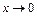 и применим правило Лопиталя:
и применим правило Лопиталя:
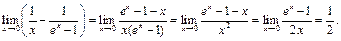
Пример 11. Найти 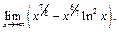
Преобразуем данную функцию:
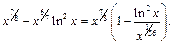
Рассмотрим 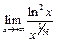 и применим правило Лопиталя последовательно два раза:
и применим правило Лопиталя последовательно два раза:
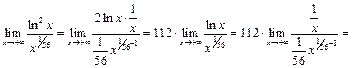
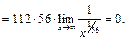 Следовательно,
Следовательно,
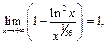 а тогда
а тогда 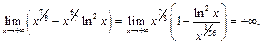
В примерах 12-14 требуется раскрыть неопределённость вида 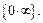
Пример 12. Найти 
Сведя неопределённость 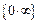 к неопределённости
к неопределённости 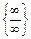 , применим правило Лопиталя последовательно два раза:
, применим правило Лопиталя последовательно два раза: 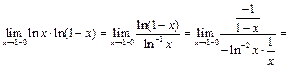

Пример 13. Найти 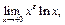
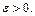
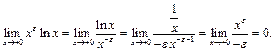
Пример 14. Найти 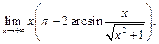
Сделаем замену переменной 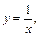 если
если 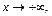 то
то 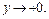 Тогда
Тогда 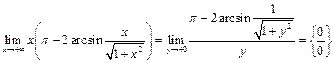 .
.
Применяя к полученному пределу правило Лопиталя, будем иметь: 
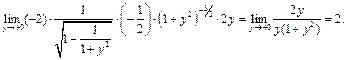
В примерах 15-20 для раскрытия неопределённостей вида 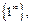
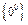 и
и 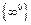 воспользуемся логарифмическим тождеством
воспользуемся логарифмическим тождеством 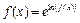 и сведём вычисление предела к раскрытию неопределённости
и сведём вычисление предела к раскрытию неопределённости 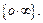
Пример 15. Найти 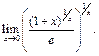
Применяя логарифмическое тождество, придём к вычислению следующего предела:
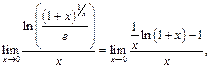 для которого после двукратного применения правила Лопиталя получим:
для которого после двукратного применения правила Лопиталя получим:
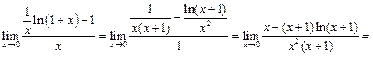
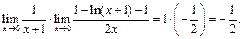
Тогда 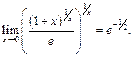
Пример 16. Найти 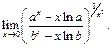
C помощью логарифмического тождества преобразуем неопределённость 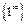 к неопределённости вида
к неопределённости вида 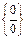 , к которой применим затем правило Лопиталя и следствие из 2-го замечательного предела:
, к которой применим затем правило Лопиталя и следствие из 2-го замечательного предела:
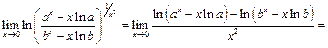

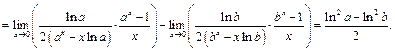 Тогда
Тогда 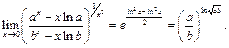
Пример 17. Найти 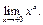
С использованием результата примера 13 получим:

Пример 18. Найти 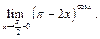
Полагая 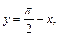 получим:
получим: 
Так как 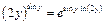 и
и 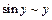 при
при 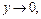 то согласно примеру 13 будем иметь:
то согласно примеру 13 будем иметь: 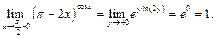
Пример 19. Найти 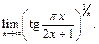
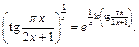 Согласно правилу Лопиталя:
Согласно правилу Лопиталя:
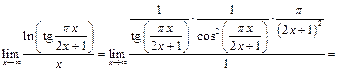
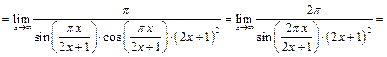

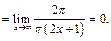
Следовательно, 
Пример 20. Найти 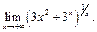
 Тогда по правилу Лопиталя и с использованием примера 8 будем иметь:
Тогда по правилу Лопиталя и с использованием примера 8 будем иметь:
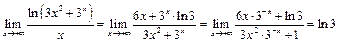 .
.
Поэтому 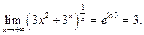
Пример 21. Найти 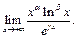
Пусть сначала 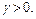 Если
Если 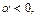
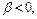 то функции
то функции 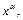
 и
и  есть бесконечно малые при
есть бесконечно малые при 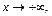 а следовательно,
а следовательно, 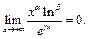 Если же
Если же 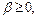 а
а 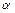 - любое, то
- любое, то 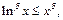 откуда следует, что:
откуда следует, что:
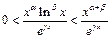 , а
, а 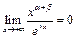 (пример 8). Согласно принципу двустороннего ограничения
(пример 8). Согласно принципу двустороннего ограничения 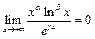 . Итак, доказано: при
. Итак, доказано: при  и
и 
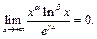
Пусть теперь 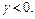 Так как по доказанному выше
Так как по доказанному выше 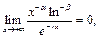 то обратная величина является бесконечно большой при
то обратная величина является бесконечно большой при 
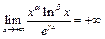 для
для 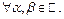
|
|
|
Если же 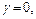 то имеем:
то имеем: 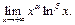 Сделаем замену
Сделаем замену  будем иметь:
будем иметь:  Тогда:
Тогда:
1) 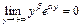 при
при 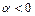 и
и 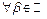 и при
и при 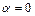 и
и 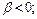
2) 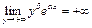 при
при 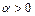 и
и 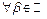 и при
и при 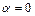 и
и 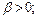
3) 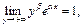 если
если 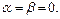
Окончательно, предел равен нулю, если 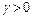 (
(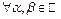 ) либо
) либо 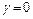 (
(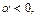
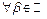 или
или 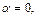
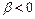 );
);
предел равен 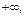 если
если 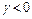 (
(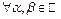 ) либо
) либо 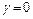 (
(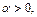
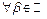 или
или 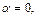
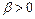 ); предел равен 1, если
); предел равен 1, если 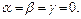
Применение правила Лопиталя не всегда возможно, поэтому надо внимательно следить за выполнением условий теоремы.
Пример 22. Объяснить, почему следующие пределы не могут быть найдены по правилу Лопиталя и найти их, если они существуют: 1) 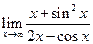 ; 2)
; 2)  .
.
Правило Лопиталя в обоих случаях неприменимо, так как предел отношения производных не существует, однако с использованием леммы о бесконечно малых легко получить, что 1) 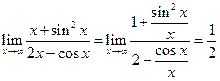 ;
;
2) 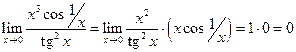 .
.
Пример 23. Исследовать возможность применения правила Лопиталя к следующему пределу: 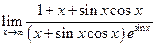 .
.
Условия теоремы не выполнены, ибо производные 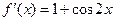 и
и 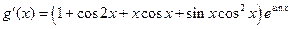 обращаются в нуль одновременно в любой окрестности точки
обращаются в нуль одновременно в любой окрестности точки 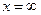 , если
, если 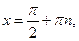
 , поэтому правило Лопиталя использовать нельзя. Отметим, что данный предел не существует, что легко получить по определению Гейне:
, поэтому правило Лопиталя использовать нельзя. Отметим, что данный предел не существует, что легко получить по определению Гейне:
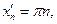
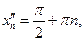
 , если
, если  , то и
, то и 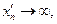
 ; при этом
; при этом  , а
, а 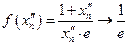 при
при  .
.
|
|
|
|
|
Дата добавления: 2015-05-31; Просмотров: 921; Нарушение авторских прав?; Мы поможем в написании вашей работы!