
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Решение. 1. Разобьем всю вариацию объёмом на частичных интервалов равной длины и посчитаем частоты попадания наблюдаемых значений в частичные интервалы
|
|
|
|
1. Разобьем всю вариацию объёмом 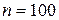 на
на 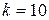 частичных интервалов равной длины и посчитаем частоты попадания наблюдаемых значений в частичные интервалы.
частичных интервалов равной длины и посчитаем частоты попадания наблюдаемых значений в частичные интервалы.
Длину интервала находим по формуле 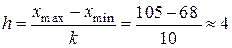 .
.
За начало первого интервала примем 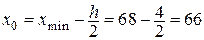 . Получим последовательность интервалов: [66; 70], (70; 74], …, (102; 106].
. Получим последовательность интервалов: [66; 70], (70; 74], …, (102; 106].
Составим вариационный ряд частот и относительных частот:
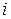
| интервал
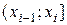
| середина
интервала
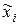
| частота
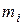
| относительная частота
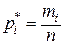
|
| [66; 70] | 0,04 | |||
| (70; 74] | 0,03 | |||
| (74; 78] | 0,07 | |||
| (78; 82] | 0,16 | |||
| (82; 86] | 0,18 | |||
| (86; 90] | 0,20 | |||
| (90; 94] | 0,15 | |||
| (94; 98] | 0,07 | |||
| (98; 102] | 0,06 | |||
| (102; 106] | 0,04 | |||
| Σ | – | – |
Отметим, что 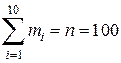 – объём выборки;
– объём выборки; 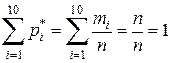 .
.
Статистическое распределение выборки является оценкой неизвестного распределения. В частности, относительные частоты 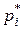 являются статистическими аналогами вероятностей полной группы несовместных событий.
являются статистическими аналогами вероятностей полной группы несовместных событий.
2. Вторым этапом обработки статистических данных является построение полигона, гистограммы относительных частот и эмпирической функции распределения.
а) Полигон относительных частот вариационного ряда – ломаная линия, соединяющая точки 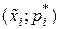 .
График полигона представлен на рис. 11. .
График полигона представлен на рис. 11.
| 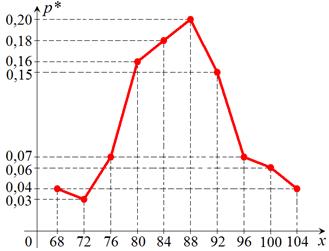 Рис. 11
Рис. 11
|
Полигон относительных частот является статистическим аналогом многоугольника распределения дискретной случайной величины Х.
б) Гистограмма относительных частот изображается только для интервального ряда и имеет вид ступенчатой фигуры (рис. 12).
На каждом частичном интервале строим прямоугольник высотой 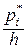 . .
| 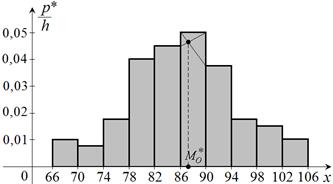 Рис. 12
Рис. 12
|
Гистограмма относительных частот является статистическим аналогом дифференциальной функции распределения (плотности) 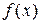 непрерывной случайной величины Х.
непрерывной случайной величины Х.
в) График эмпирической функции распределения 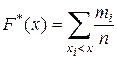 непрерывной случайной величины X совпадает с кумулятой (графиком накопленных частот).
непрерывной случайной величины X совпадает с кумулятой (графиком накопленных частот).
Отметим на плоскости точки, соответствующие значениям функции  на концах интервалов, и соединим их отрезками прямых (рис. 13).
на концах интервалов, и соединим их отрезками прямых (рис. 13).
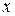
| 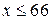
| 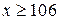
| |||||||||

| 0,04 | 0,07 | 0,14 | 0,30 | 0,48 | 0,68 | 0,83 | 0,90 | 0,96 |
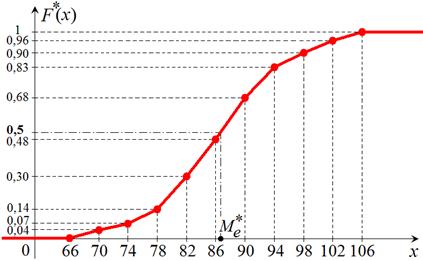
Рис. 13
Эмпирическая функция распределения 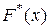 является статистическим аналогом интегральной функции распределения
является статистическим аналогом интегральной функции распределения 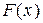 случайной величины Х.
случайной величины Х.
3. Найдем числовые характеристики выборки.
Выборочные характеристики – это функции наблюдений, приближённо оценивающие соответствующие числовые характеристики случайной величины.
1) Мода 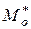 находится внутри интервала, для которого соответствующая частота максимальна. В нашем случае
находится внутри интервала, для которого соответствующая частота максимальна. В нашем случае 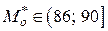 , при этом
, при этом 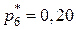
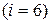 .
.
Моду можно определить на чертеже гистограммы (рис. 12) или вычислить по формуле
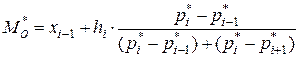 ,
,
где 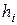 – длина частичного интервала
– длина частичного интервала 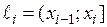 ,
,
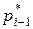 – частость, соответствующая предыдущему частичному интервалу
– частость, соответствующая предыдущему частичному интервалу 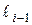 ,
,
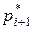 – частость, соответствующая следующему частичному интервалу
– частость, соответствующая следующему частичному интервалу 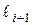 .
.
Тогда получим
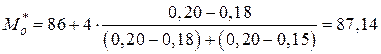 .
.
2) Медиана 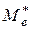 интервального вариационного ряда принадлежит тому частотному интервалу, для которого накопленная частота составляет половину или больше половины всей суммы частот, а предыдущая накопленная частота меньше половины всей суммы частот. Геометрически прямая
интервального вариационного ряда принадлежит тому частотному интервалу, для которого накопленная частота составляет половину или больше половины всей суммы частот, а предыдущая накопленная частота меньше половины всей суммы частот. Геометрически прямая 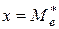 делит площадь гистограммы пополам.
делит площадь гистограммы пополам.
Медиана может быть приближённо найдена на чертеже графика 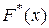 (рис. 13), как значение признака, для которого
(рис. 13), как значение признака, для которого 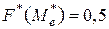 . Для данного вариационного ряда значение
. Для данного вариационного ряда значение 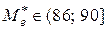 .
.
Значение 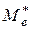 вычисляем по формуле
вычисляем по формуле
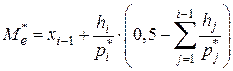 .
.
Тогда получим
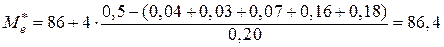 .
.
3) Для нахождения выборочной средней 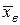 , выборочной дисперсии
, выборочной дисперсии 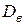 , выборочного среднего квадратического отклонения
, выборочного среднего квадратического отклонения 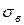 (статистические аналоги соответствующих числовых характеристик случайной величины) заполним вспомогательную таблицу.
(статистические аналоги соответствующих числовых характеристик случайной величины) заполним вспомогательную таблицу.
| i | 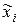
| 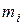
| 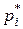
| 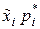
| 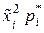
|
| 0,04 | 2,72 | 184,96 | |||
| 0,03 | 2,16 | 155,52 | |||
| 0,07 | 5,32 | 404,32 | |||
| 0,16 | 12,80 | 1024,00 | |||
| 0,18 | 15,12 | 1270,08 | |||
| 0,2 | 17,60 | 1548,80 | |||
| 0,15 | 13,80 | 1269,60 | |||
| 0,07 | 6,72 | 645,12 | |||
| 0,06 | 6,00 | 600,00 | |||
| 0,04 | 4,16 | 432,64 | |||
| Σ | – | 86,4 | 7535,04 |
Находим выборочное среднее:
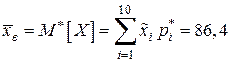 ;
;
выборочную дисперсию:
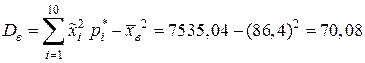 ;
;
выборочное среднее квадратическое отклонение: 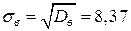 ;
;
исправленную выборочную дисперсию:
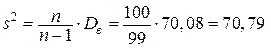 ;
;
исправленное выборочное среднее квадратическое отклонение
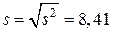 .
.
Т. к. число наблюдений 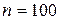 достаточно велико, то вместо
достаточно велико, то вместо 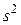 можно использовать неисправленную выборочную дисперсию
можно использовать неисправленную выборочную дисперсию 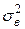 .
.
4. Точечной оценкой математического ожидания 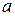 является средняя выборочная
является средняя выборочная 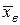 , тогда полагаем
, тогда полагаем  ; точечной оценкой генерального среднего квадратического отклонения
; точечной оценкой генерального среднего квадратического отклонения 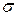 является исправленное выборочное среднее квадратическое отклонение, т. е.
является исправленное выборочное среднее квадратическое отклонение, т. е.  .
.
а) Вид гистограммы относительных частот напоминает график плотности функции 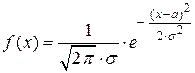 нормального распределения непрерывной случайной величины
нормального распределения непрерывной случайной величины 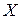 .
.
Построим на одном чертеже с гистограммой относительных частот  (рис. 11) её теоретический аналог
(рис. 11) её теоретический аналог 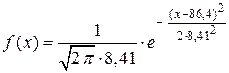 (рис. 14).
(рис. 14).
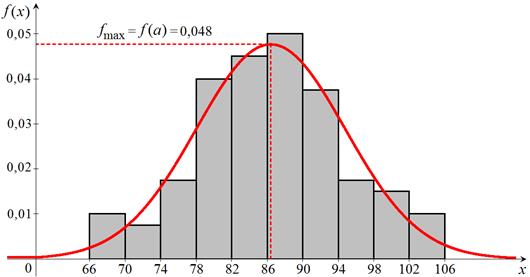
Рис. 14
б) Вид эмпирической функции распределения 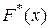 напоминает интегральную функцию
напоминает интегральную функцию 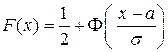 нормального распределения. Построим на одном чертеже с эмпирической функцией
нормального распределения. Построим на одном чертеже с эмпирической функцией 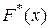 (рис. 12) её теоретический аналог
(рис. 12) её теоретический аналог 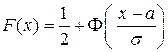 , где
, где 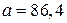 ,
, 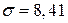 (рис. 15).
(рис. 15).
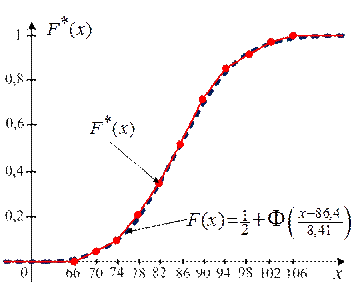
|
| Рис. 15 |
5. По виду гистограммы и функции 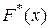 выдвигаем основную (нулевую) гипотезу
выдвигаем основную (нулевую) гипотезу 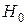 : «Генеральная совокупность распределена по нормальному закону с параметрами
: «Генеральная совокупность распределена по нормальному закону с параметрами 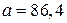 ,
, 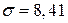 » и альтернативную гипотезу
» и альтернативную гипотезу 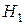 : «Генеральная совокупность не распределена по нормальному закону».
: «Генеральная совокупность не распределена по нормальному закону».
6. Проверим выполнение правила «трёх сигм»:
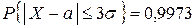 ,
,
которое требует, чтобы в 99,73 % значения случайной величины, распределенной по нормальному закону, попадали на отрезок 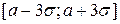 .
.
В нашем случае: 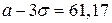 ,
, 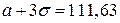 , отсюда получаем, что интервал опытных данных
, отсюда получаем, что интервал опытных данных  . Таким образом, найденный промежуток полностью накрыл наши статистические значения.
. Таким образом, найденный промежуток полностью накрыл наши статистические значения.
Т. к. условие правила «трёх сигм» выполняется, то есть основание предполагать, что изучаемое распределение является нормальным.
7. Проверим соответствие гипотезы 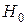 опытным данным.
опытным данным.
Для этого необходимо вычислить теоретические вероятности 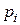 и выравнивающие частоты
и выравнивающие частоты 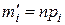 .
.
Необходимым условием применения критерия Пирсона является наличие в каждом из интервалов не менее 5 наблюдений (т. е. 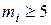 ). Т. к. число наблюдений в крайних интервалах меньше 5, то объединим их с соседними. Получим следующий ряд распределения:
). Т. к. число наблюдений в крайних интервалах меньше 5, то объединим их с соседними. Получим следующий ряд распределения:
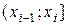
| [64; 74] | (74; 78] | (78; 82] | (82; 86] | (86; 90] | (90; 94] | (94; 98] | (98; 106] |
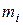
|
Найдём интервальные вероятности 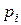 . Т. к. случайная величина определена на интервале
. Т. к. случайная величина определена на интервале 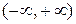 , то крайние промежутки в ряде распределения заменяем, соответственно на
, то крайние промежутки в ряде распределения заменяем, соответственно на 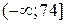 и
и 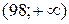 (рис. 16).
(рис. 16).
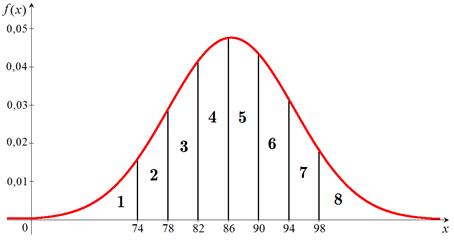
Рис. 16
Искомые вероятности вычисляем по формуле
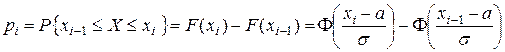 .
.
Используя таблицу приложения 2 и свойства функции Лапласа, находим:
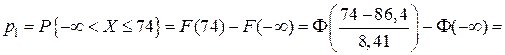
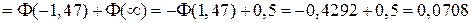 ;
;
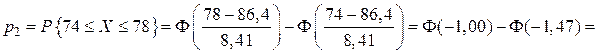
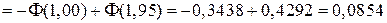 ;
;
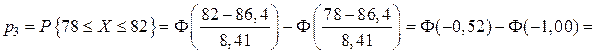
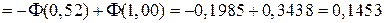 ;
;
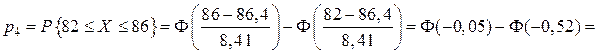
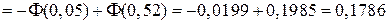 ;
;
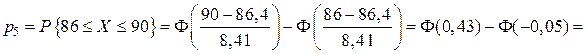
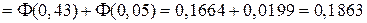 ;
;
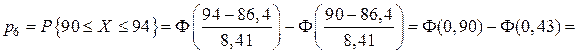
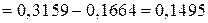 ;
;
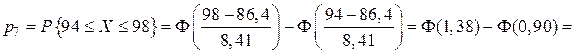
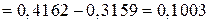 ;
;
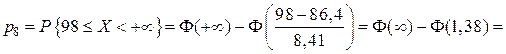
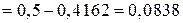 .
.
Для дальнейших расчётов заполним вспомогательную таблицу:
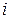
| интервал
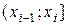
| частота
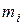
| теоретическая частота
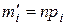
| 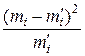
|
(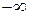 ; 74] ; 74]
| 7,08 | 0,0009 | ||
| (74; 78] | 8,54 | 0,2777 | ||
| (78; 82] | 14,53 | 0,1487 | ||
| (82; 86] | 17,86 | 0,0011 | ||
| (86; 90] | 18,63 | 0,1007 | ||
| (90; 94] | 14,95 | 0,0002 | ||
| (94; 98] | 10,03 | 0,9153 | ||
(98; 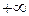 ) )
| 8,38 | 0,3132 | ||
| Σ | – | 1,7578 |
Наблюдаемое значение критерия согласия Пирсона (итоговая строка таблицы) 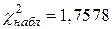 .
.
По таблице приложения 3 критических точек распределения 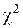 , по заданному уровню значимости
, по заданному уровню значимости 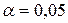 и числу степеней свободы
и числу степеней свободы 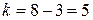 найдём критическое значение
найдём критическое значение 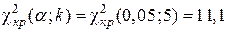 .
.
Т. к. 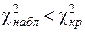 , то нет оснований отвергнуть проверяемую нулевую гипотезу. Т. е. принимаем предположение, что статистические данные распределены по нормальному закону с параметрами
, то нет оснований отвергнуть проверяемую нулевую гипотезу. Т. е. принимаем предположение, что статистические данные распределены по нормальному закону с параметрами 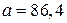 и
и 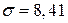 .
.
8. a) Построим на одном чертеже полигон эмпирических относительных частот 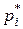 и кривую распределения и кривую распределения  (рис. 17). (рис. 17).
| 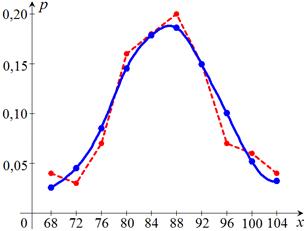 Рис. 17
Рис. 17
|
 – кривая – кривая 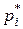 . .
| |
 – кривая – кривая  . .
|
Полигон относительных частот 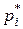 представляет данные, взятые по выборке. Кривая
представляет данные, взятые по выборке. Кривая  выравнивает эмпирические данные, тем самым приближая распределение генеральной совокупности к нормальному.
выравнивает эмпирические данные, тем самым приближая распределение генеральной совокупности к нормальному.
б) Построим на одном чертеже гистограмму теоретических вероятностей (относительных частот)  и график функции
и график функции 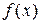 (рис. 18).
(рис. 18).
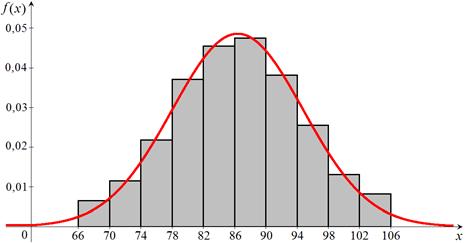
Рис. 18
9. Т. к. 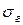 неизвестно, то доверительный интервал для генеральной средней
неизвестно, то доверительный интервал для генеральной средней 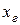 имеет вид
имеет вид
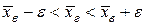 ,
,
где величина 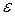 определяется по формуле:
определяется по формуле: 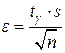 .
.
Значение 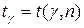 находим в таблице приложения 6 по заданному уровню надёжности
находим в таблице приложения 6 по заданному уровню надёжности 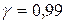 и
и 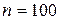 :
: 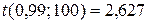 .
.
Тогда 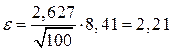 .
.
Таким образом, получаем доверительный интервал для 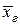 :
:

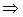
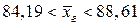 .
.
Это означает, что в 99 % случаев истинное значение генеральной средней 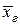 находится в промежутке
находится в промежутке 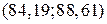 .
.
Доверительный интервал для генерального среднего квадратического отклонения определяется следующим образом:
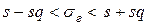 .
.
По таблице приложения 7 величина 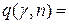
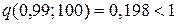 . Отсюда получаем:
. Отсюда получаем:
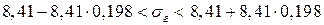
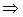
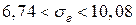 .
.
Это означает, что в 99 % истинное значение генерального среднего квадратического отклонения 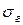 находится промежутке
находится промежутке
(6,74; 10,08).
Приложение 1
Приложение 2
Ряд Тейлора
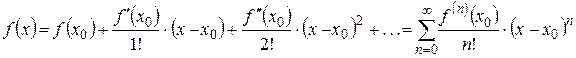
Разложение некоторых элементарных функций в ряд Маклорена
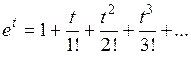
| 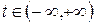
|
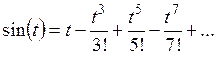
| 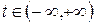
|
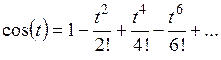
| 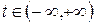
|
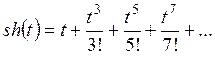
| 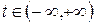
|
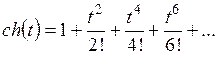
| 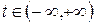
|
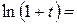 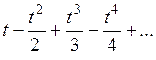
| 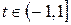
|
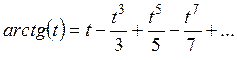
| 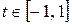
|
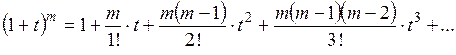
| 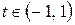
|
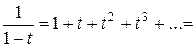
| 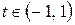
|
Приложение 3.
Приложение 4.
|
|
|
|
|
Дата добавления: 2015-06-26; Просмотров: 2299; Нарушение авторских прав?; Мы поможем в написании вашей работы!