Нормальный закон распределения

Нормальный закон (дискретный вариант) является асимптотическим приближением биномиального закона пр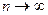и и 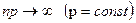. Неограниченно уменьшая интервал между соседними значениями случайной величины, можно от дискретного распределения перейти к непрерывному. Однако нормальный закон возникает в гораздо более широких условиях, чем указанные выше. Поэтому он играет особую роль в вероятностных расчетах и является наиболее известной статистической моделью, используемой для описания физических явлений и систем.

Теоретическим обоснованием роли и условий возникновения нормального распределения (распределения Гаусса) является центральная предельная теорема А.М. Ляпунова - один из наиболее важных результатов математической статистики. Смысл этой теоремы состоит в следующем.

Распределение суммы независимых или слабо зависимых, равномерно малых (примерно одинаковых) слагаемых при неограниченном увеличении их числа, стремится (приближается, сходится) к нормальному распределению, независимо от того, какие законы распределения имеют эти слагаемые.

В соответствии с этой теоремой, если случайное явление происходит как следствие действия большого числа независимых слабых случайных факторов, среди которых нет превалирующих, то для описания этого явления можно в качестве модели выбрать нормальное распределение. Такие условия на практике встречаются очень часто, что и обусловливает широкое распространение этого закона. Кроме того, нормальный закон обладает рядом замечательных свойств, которые упрощают теоретические построения. Поэтому даже при наличии некоторых отступлений реального распределения от нормального, его все же стремятся аппроксимировать нормальным распределением.

Нормальным распределением вероятностей непрерывной сл.в. x называется такое распределение, которое описывается п.в. вида

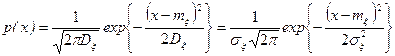, (2.14.1)

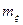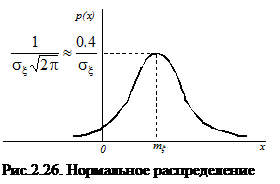
где и 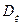- два параметра распределения. График плотности вероятности нормального распределения приведен на рис. 2.26.

Функция (1) может служить п.в. так как она неотрицательна и удовлетворяет условию нормировки: и 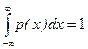. Чтобы доказать последнее утверждение, проинтегрируем (1) в бесконечных пределах, произведя при этом замену переменной 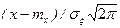. Тогда будем иметь

,

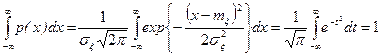где 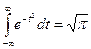- интеграл Пуассона.

Для выяснения теоретико-вероятностного смысла параметров распределения функции (1), вычислим м.о. и дисперсию сл. в. x:

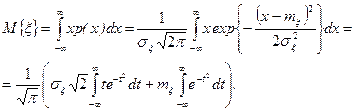
Первый интеграл равен нулю, как интеграл от нечетной функции в бесконечных пределах. Поэтому .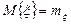

Таким образом, параметр 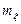в выражении (1) имеет смысл м.о. сл.в. x. Путем интегрирования по частям, нетрудно показать, что

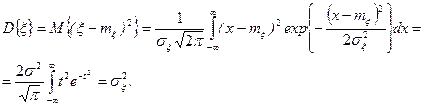Следовательно, параметр 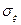в выражении (1) имеет смысл среднего квадратического отклонения нормально распределенной сл.в., а 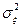- смысл дисперсии.

Основные свойства нормального распределения.

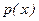1. Нормальная п.в. симметрична относительно прямой 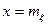, причем при 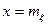максимальна и равна 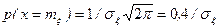. Кривая 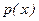имеет один максимум, так что мода, медиана и м.о. совпадают, т.е. .

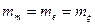2. При 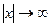ветви кривой асимптотически приближаются к оси абсцисс.

3. Нормальное распределение зависит от двух параметров 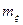и 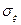и полностью описывается ими. Изменение при = const приводит к смещению кривой вдоль оси абсцисс без изменения формы кривой (рис.2.27). Параметр 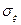характеризует форму кривой: при уменьшени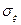и и 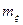= const максимум 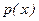увеличивается, кривая сужается и переходит в пределе при 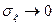в дельта - функцию 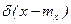. Наоборот, увеличение 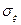приводит к уменьшению максимума и расширению кривой, что следует из условия нормировки (рис.2.28). Постоянную величину с можно трактовать как нормально распределенную сл.в. с нулевой дисперсией.

4. График 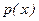имеет две точки перегиба: одна отвечает значению 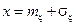, а другая - значению 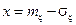(рис.2.27).

5. Функция распределения 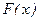, соответствующая п.в. (1) имеет вид

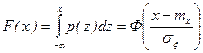, (2.14.2)

где

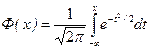(2.14.3)

- табулированный интеграл вероятности (функция Лапласа), причем

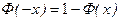. (2.14.4)

В литературе для удобства решения конкретных задач встречаются другие формы табулированного интеграла вероятности, например,

, ,

.

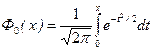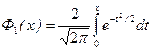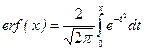Эти выражения связаны между собой следующими соотношениями:

, ,

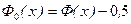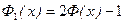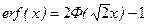
или

, ,

.

При пользовании таблицей интеграла вероятности, следует учитывать, в какой форме он задан.

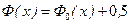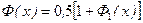Получим формулу (2), используя замену переменной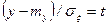

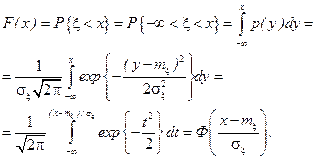
Функция (3) зависит только от одной переменной x и представляет собой функцию распределения сл.в. 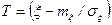, имеющей нормальное распределение с параметрам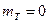и и .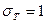

Графики функций p(x), F(x), p(t), и F(t) приведены соответственно на рис.2.29 и рис.2.30.

6. Вероятность попадания cл.в. x, распределенной по нормальному закону с параметрам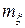и и 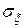, в интервал [ a, b) равна

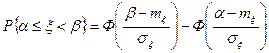. (2.14.5)

В самом деле

.

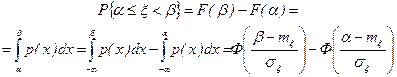Так, например

,

,

.

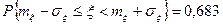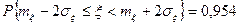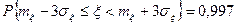Значение функции p(x) при 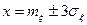равно 0,0044/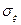, т.е. почти в 100 раз меньше, чем при максимуме, где оно равно 0,4/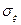. Это означает, что кривая p(x) практически полностью расположена на интервале 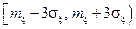. Иначе говоря, практически можно считать достоверным нахождение сл.в. на этом интервале.

Это свойство известно под названием "правило трех сигм". Сущность этого правила состоит в следующем. Если сл.в. x распределена нормально, то абсолютная величина ее отклонения от м.о. 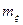- не превосходит утроенного значения :

.

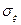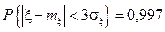Правилом трех сигм следует руководствоваться при проведении экспериментов со сл.пр., например, при аппроксимации вольтамперных характеристик транзисторов, расчетах полосы пропускания приемников и т.д.

Пример 2.14.1. Случайная величина x распределена по нормальному закону с параметрами 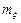=1, 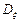=4. Требуется найти вероятность того, что в результате четырех независимых измерений сл.в. x точно три раза примет значение, принадлежащее интервалу [2, 3).

Воспользовавшись формулой (5), найдем вначале вероятность

.

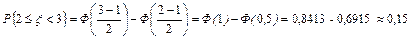Далее, используя формулу Бернулли (2.12.1), при n =4, k =3, p =0,15, q =1-0,15=0,85, получим

.

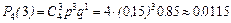Пример 2.14.2. Какой средней квадратической ошибкой должен обладать радиовысотомер, чтобы с вероятностью 0,9 ошибка x с нормальным распределением при измерении высоты не превышала по абсолютной величине 50 м. Систематическая ошибка отсутствует.

Пусть x -ошибка измерения. По условию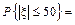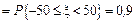. Для нормального закона имеем:

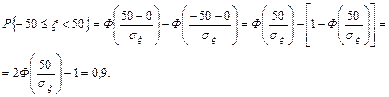
Тогда 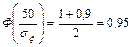. По таблице по известному значению интеграла вероятности находим значение аргумента: при Ф =0,95 имеем 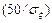=1,65. Следовательно, 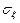=31м.

Пусть теперь 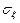=40 м, систематическая ошибка измерения высоты 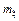=20 м. Найдем вероятность того, что измеренное значение высоты будет отличаться от истинного не более, чем на 60 м. В этом случае

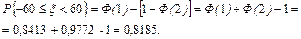
Область применения нормального закона при различных вероятностных расчетах весьма широка. Он используется для описания результатов измерения, случайных сигналов и шумов в радиоприемниках, времени безотказной работы систем различного назначения и т.д.

Кроме того, имеется ряд распределений, которые тесно связаны с нормальным: логарифмически нормальное, распределение Релея, распределение Стьюдента и т.д.

Рассмотрим, например, "хи-квадрат" распределение, которое широко используется в математической статистике.

Пусть x_i (i =1, 2,..., n) - гауссовские не зависимые сл.в. с нормальным распределением, причем м.о. каждой из них равно нулю, а среднее квадратическое отклонение - единице. Тогда сумма квадратов этих величин

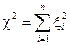
распределена по закону 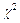("хи-квадрат") с k=n степенями свободы. Плотность этого распределения имеет вид

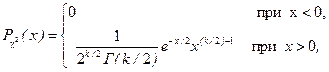(2.14.6)

где 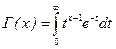- гамма-функция.

Из формулы видно, что -распределение определяется одним параметром - числом степеней свободы k:. С увеличением числа степеней свободы распределение приближается к нормальному.

Дата добавления: 2014-01-03