
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Решение.
|
|
|
|
Решение.
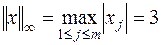
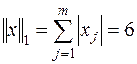
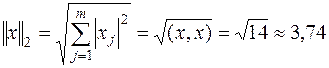
Пример 6.2. Дана матрица 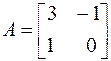 . Найти её нормы, определённые по (6.5), (6.6), (6.7).
. Найти её нормы, определённые по (6.5), (6.6), (6.7).
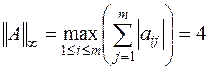
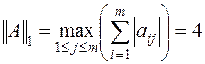
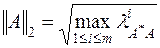
Для вычисления последней нормы найдём матрицу 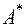 , сопряжённую матрице
, сопряжённую матрице 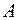 , перемножим их и найдём наибольшее собственное число произведения:
, перемножим их и найдём наибольшее собственное число произведения:
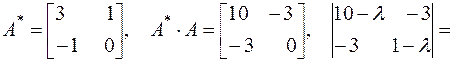
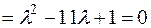 ,
, 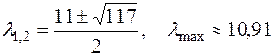 ,
, 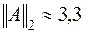
Следуя [9], докажем теперь, что норма матрицы 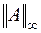 , определяемая равенством (6.5), является согласованной с нормой вектора
, определяемая равенством (6.5), является согласованной с нормой вектора 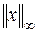 , определяемой равенством (6.2), в соответствии с определением согласованности, которое даётся равенством (6.1).
, определяемой равенством (6.2), в соответствии с определением согласованности, которое даётся равенством (6.1).
Доказательство. Рассмотрим вектор 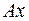 . По определению (6.2) имеем:
. По определению (6.2) имеем:
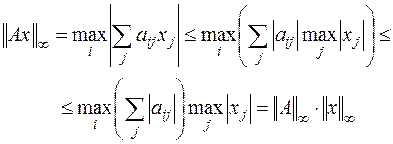
Отсюда следует, что имеет место неравенство
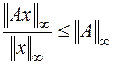 (6.8)
(6.8)
Мы доказали, что значение 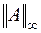 , которое вычисляется по формуле (6.5), является какой-то из верхних границ для отношения
, которое вычисляется по формуле (6.5), является какой-то из верхних границ для отношения 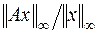 , где
, где 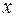 - любой ненулевой вектор. Для того, чтобы доказать, что норма (6.5) является согласованной с нормой (6.2), требуется показать, что она является супремумом, т.е. наименьшей из всех верхних границ, что может иметь место хотя бы для одного какого-либо вектора
- любой ненулевой вектор. Для того, чтобы доказать, что норма (6.5) является согласованной с нормой (6.2), требуется показать, что она является супремумом, т.е. наименьшей из всех верхних границ, что может иметь место хотя бы для одного какого-либо вектора 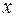 . Предположим, что
. Предположим, что 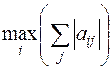 достигается при
достигается при 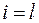 , т.е.
, т.е.
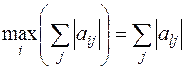 (6.9)
(6.9)
Введём некоторый вектор 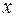 следующим образом:
следующим образом:
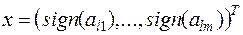 (6.10)
(6.10)
Тогда по определению (6.2) имеем:
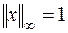 (6.11)
(6.11)
Снова рассмотрим вектор 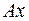 , теперь - для вектора (6.10). По формуле (6.2) получим:
, теперь - для вектора (6.10). По формуле (6.2) получим:
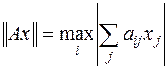 (6.12)
(6.12)
Если в правую часть (6.12) вместо индекса 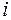 подставить какой-то произвольный номер, то это выражение может только уменьшиться. Положим
подставить какой-то произвольный номер, то это выражение может только уменьшиться. Положим 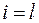 . Продолжая (6.12), с учётом (6.10), (6.11) и (6.9) последовательно находим
. Продолжая (6.12), с учётом (6.10), (6.11) и (6.9) последовательно находим
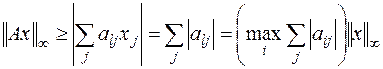 .
.
Отсюда получаем
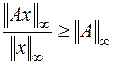 (6.13)
(6.13)
Неравенство (6.13) имеет место для специально подобранного вектора 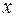 , который определяется равенством (6.10). В то же время, неравенство (6.8) выполняется для любого вектора
, который определяется равенством (6.10). В то же время, неравенство (6.8) выполняется для любого вектора 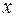 , в т.ч. и для вектора (6.10). Отсюда, сравнивая (6.8) и (6.13), получаем то, что и требовалось доказать:
, в т.ч. и для вектора (6.10). Отсюда, сравнивая (6.8) и (6.13), получаем то, что и требовалось доказать:
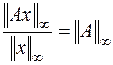
Доказательства согласованности норм (6.3), (6.6) и (6.4), (6.7) также не вызывают затруднений и здесь не приводятся (см. [9]).
|
|
|
Приведём также без доказательства важный результат ([9]). Если 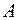 - симметричная матрица, то для неё
- симметричная матрица, то для неё
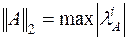
| (6.14) |
И, далее, модуль любого собственного значения матрицы 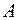 не больше любой ее нормы.
не больше любой ее нормы.
6.3. Погрешность приближённого решения системы линейных алгебраических уравнений и обусловленность матриц. Собственно методы решения СЛАУ мы рассмотрим уже в ближайших параграфах. А здесь, следуя [9], постараемся ответить на вопрос, как на погрешность решения СЛАУ влияют ошибки в задании коэффициентов матрицы системы и компонентов вектора её правой части.
Итак, решается СЛАУ
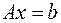
| (6.15) | |
Здесь и далее в учебнике 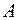 - матрица СЛАУ размерности - матрица СЛАУ размерности 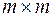 , её коэффициенты будем обозначать через , её коэффициенты будем обозначать через 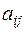 , , 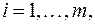 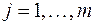 ; ; 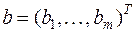 - вектор правой части СЛАУ. Пусть, однако, матрица - вектор правой части СЛАУ. Пусть, однако, матрица 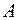 и вектор и вектор 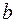 известны с погрешностями, т.е. на самом деле вместо (6.15) должно быть известны с погрешностями, т.е. на самом деле вместо (6.15) должно быть
| ||
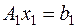 , , 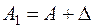 , , 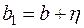 (6.16) (6.16)
| ||
Здесь 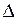 - матрица ошибок задания матрицы коэффициентов - матрица ошибок задания матрицы коэффициентов 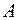 , а , а 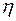 - вектор ошибок задания вектора правой части - вектор ошибок задания вектора правой части 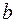 . Пусть известны нормы . Пусть известны нормы 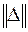 и и 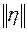 . Требуется оценить погрешность решения. Обозначим через . Требуется оценить погрешность решения. Обозначим через 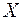 решение (6.15), через решение (6.15), через 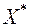 - решение (6.16), через - решение (6.16), через 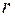 = =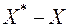 - погрешность решения СЛАУ. Подставим - погрешность решения СЛАУ. Подставим 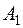 , , 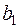 и и 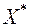 в первое равенство (6.16): в первое равенство (6.16):
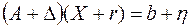
| ||
Учитывая (6.16), получим
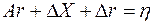
откуда
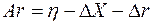
Умножая последнее равенство на 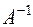 слева, находим
слева, находим
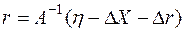
| (6.17) |
Т.к. 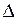 и
и 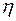 - погрешности, которые предполагаются малыми, то можно ожидать малости и от
- погрешности, которые предполагаются малыми, то можно ожидать малости и от 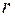 . Следовательно, их произведением в (6.17) можно пренебречь. Получаем
. Следовательно, их произведением в (6.17) можно пренебречь. Получаем
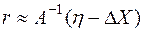 (6.18)
(6.18)
В частности, при точном задании матрицы коэффициентов (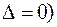 имеем:
имеем:
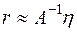 (6.19)
(6.19)
Применяя норму к обеим частям (6.18), находим оценку погрешности
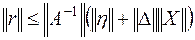 . .
| (6.20) |
А из (6.19) получаем
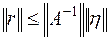 (6.21)
(6.21)
Формула (6.21) позволяет оценить погрешность решения СЛАУ в зависимости от погрешности её правой части. Однако мы видим, что если обе части исходной системы (6.15) умножить на один и тот же сомножитель, оценка (6.21) увеличится. Другими словами, это неравенство, которое описывает абсолютную погрешность решения, зависит от масштаба коэффициентов системы и не слишком информативно. Здесь более показательным будет получение и использование зависимости между относительными погрешностями правой части СЛАУ и её решения. Для этого определим показатель, который называется мерой обусловленности системы, по формуле:
|
|
|
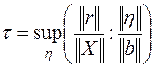 (6.22)
(6.22)
Как видно, это есть значение отношения относительной погрешности решения к относительной погрешности правой части. Вынося в правой части (6.22) за знак супремума то, что на него не влияет, получим:
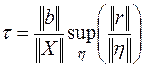 (6.23)
(6.23)
Из определения 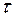 следует, что это есть наименьшее из всех верхних границ указанного отношения, и это равенство может достигаться при каком-либо значении
следует, что это есть наименьшее из всех верхних границ указанного отношения, и это равенство может достигаться при каком-либо значении 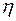 . Ну а для произвольных
. Ну а для произвольных 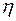 имеет место неравенство
имеет место неравенство
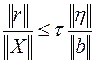
| (6.24) |
При 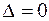 выше мы имели
выше мы имели 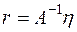 . Следовательно, по определению (6.1) согласованности норм в пространствах векторов и матриц имеем:
. Следовательно, по определению (6.1) согласованности норм в пространствах векторов и матриц имеем:
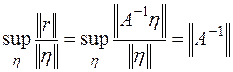
Тогда из (6.23) получаем:
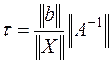 (6.25)
(6.25)
Меру обусловленности системы по формуле (6.25) оценивать достаточно сложно, т.к. в это выражение входит решение 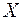 исходной системы, которое заранее неизвестно. Поэтому наряду с числом
исходной системы, которое заранее неизвестно. Поэтому наряду с числом 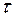 используют более грубую характеристику погрешности решения СЛАУ, которая определяется только свойствами матрицы
используют более грубую характеристику погрешности решения СЛАУ, которая определяется только свойствами матрицы 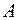 . Она называется мерой (или числом) обусловленности матрицы
. Она называется мерой (или числом) обусловленности матрицы 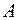 и задаётся формулой
и задаётся формулой
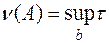 (6.26)
(6.26)
Согласно этому определению и (6.24), получаем:
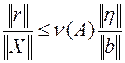
Как мы видим, число 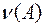 является как бы коэффициентом пропорциональности между относительной погрешностью правой части СЛАУ и относительной погрешностью решения. Таким образом, чем больше значение
является как бы коэффициентом пропорциональности между относительной погрешностью правой части СЛАУ и относительной погрешностью решения. Таким образом, чем больше значение 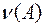 , тем хуже обстоит дело с погрешностью решения.
, тем хуже обстоит дело с погрешностью решения.
Вычислим правую часть (6.26). Применяя ещё раз определение (6.1), имеем:
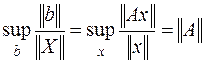
Подставляя найденное значение в (6.26), получаем:
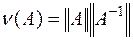 (6.27)
(6.27)
Эту формулу удобно применять для вычисления 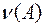 . Получим из неё ещё и оценку для
. Получим из неё ещё и оценку для 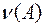 . Во-первых, воспользуемся свойством, сформулированным в конце прошлого пункта: норма матрицы не меньше любого собственного числа этой матрицы, т.е. имеет место неравенство:
. Во-первых, воспользуемся свойством, сформулированным в конце прошлого пункта: норма матрицы не меньше любого собственного числа этой матрицы, т.е. имеет место неравенство: 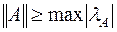 .
.
Во-вторых, вспомним, что собственные значения матриц 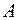 и
и 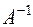 являются взаимно обратными. Отсюда имеем
являются взаимно обратными. Отсюда имеем
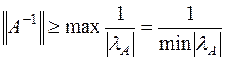 .
.
Подставляя полученные соотношения в (6.27), находим:
|
|
|
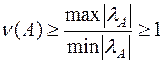 (6.28)
(6.28)
Решим ряд примеров.
Пример 6.3. Найти нормы матрицы 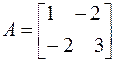 , её число обусловленности и оценку числа обусловленности.
, её число обусловленности и оценку числа обусловленности.
|
|
|
|
|
Дата добавления: 2014-01-03; Просмотров: 1505; Нарушение авторских прав?; Мы поможем в написании вашей работы!