
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Тригонометрическая форма записи комплексных чисел
|
|
|
|
2.1. Геометрическое изображение комплексного числа
Комплексное число можно изображать точками плоскости (как координаты точек плоскости в прямоугольной системе координат xОу). Согласно методу координат, с каждой точкой А плоскости Оху можно связать вектор 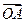 , выходящий из начала координат и оканчивающийся в точке А. Таким образом, к.число a + i×b допускает геометрическую интерпретацию как вектор
, выходящий из начала координат и оканчивающийся в точке А. Таким образом, к.число a + i×b допускает геометрическую интерпретацию как вектор 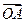 с координатами (а; b) (рис. 3.1). Координаты вектора
с координатами (а; b) (рис. 3.1). Координаты вектора 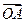 при этом будут такими же, как и координаты точки А, а именно (а; b).
при этом будут такими же, как и координаты точки А, а именно (а; b).
2.2. Геометрическая интерпретация суммы и разности комплексных чисел
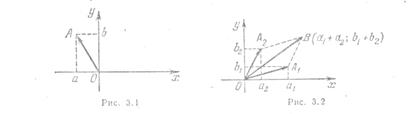
Геометрическая интерпретация к.ч. позволяет наглядно представить сумму и разность к. чисел. Пусть даны два к.ч. z1 = a1 + b1×i и z2 = a2 + b2×i. Их сумной будет к. ч. z = z1 + z2 = (a1 + a2) + i×(b1 + b2). Из свойств векторов известно, что при сложении векторов их соответственные координаты складываются. Поэтому, если вектор 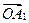 имеет координаты (a1, b1) (рис. 3.2), а вектор
имеет координаты (a1, b1) (рис. 3.2), а вектор 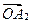 – координаты (а2, b2), то их сумма (вектор
– координаты (а2, b2), то их сумма (вектор 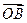 ) будет иметь координаты (a1 + a2; b1 + b2), который и является геометрической интерпретацией суммы к. ч. z1 и z2. Так как разность двух комплексных чисел z1 = a1 + b1×i и z2 = a2 + b2×i есть сумма комплексного числа z1 и числа, противоположного комплексному числу z2, то геометрически ее можно изобразить как сумму вектора
) будет иметь координаты (a1 + a2; b1 + b2), который и является геометрической интерпретацией суммы к. ч. z1 и z2. Так как разность двух комплексных чисел z1 = a1 + b1×i и z2 = a2 + b2×i есть сумма комплексного числа z1 и числа, противоположного комплексному числу z2, то геометрически ее можно изобразить как сумму вектора 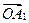 с координатами (a1, b1) и вектора
с координатами (a1, b1) и вектора 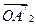 с координатами (–a2, –b2) (рис. 3.3), т. е. как вектор
с координатами (–a2, –b2) (рис. 3.3), т. е. как вектор 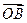 с координатами (a1 – a2; b1 – b2).
с координатами (a1 – a2; b1 – b2).
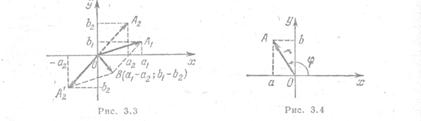
2.3. Тригонометрическая форма записи комплексного числа
Обозначим длину вектора ОА буквой r:
r = |ОА|,
а угол; который вектор образует с положительным направлением оси Ох, – через j (угол j считаем измеренным в радианах). По определению тригонометрических функций sin j = b /r, cos j = a /r. Тогда к.ч. z = a + b×i можно записать в виде
|
|
|
z = r×(соs j + i×sin j), (1)
где r = 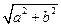 , а угол j определяется из условий
, а угол j определяется из условий
sin j = b / 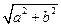 , cos j = a /
, cos j = a / 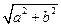 .
.
Запись к.ч. в виде (1) называется тригонометрической формой записи комплексного числа.
Действительное число r называется модулем комплексного числа и обозначается r = |z|, а угол j (измеренный в радианах) – аргументом комплексного числа z. Аргумент j комплексного числа z обозначается Arg z.
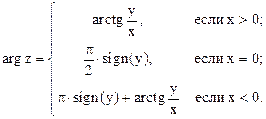
Пусть z1 и z2 – два отличных от нуля комплексных числа, записанных в тригонометрической форме:
z1 = r1×(cos j1 + i×sin j1), z2 = r2×(cos j2 + i×sin j2).
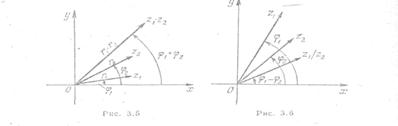
Произведение двух к.ч. z1 и z2 есть к.ч., модуль которого равен произведению модулей сомножителей, а аргумент – сумме аргументов сомножителей:
z = z1×z2 = r1×r2×[cos(j1+j2) + i×sin(j1+j2)].
Частное двух к.ч. z1 и z2 есть к. ч., модуль которого равен частному модулей делимого и делителя, а аргумент частного двух отличных от нуля к.ч. равен разности аргументов делимого и делителя:
z = z1/z2 = r1/r2×[cos(j1 – j2) + i×sin(j1 – j2)].
|
|
|
|
|
Дата добавления: 2014-01-03; Просмотров: 697; Нарушение авторских прав?; Мы поможем в написании вашей работы!