
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Iсторiя Виникнення
|
|
|
|
Історично першими виникли непозиційні системи числення. Вони ґрунтуються на кількісному підході до визначення числа, який для кодування тих чи інших кількостей застосовував особливі знаки — числа. Кожному такому знаку відповідав кількісний еквівалент. Наприклад, у так званій римській нумерації знаку X відповідала кількість елементів множини, яка дорівнювала 10.
У подальшому такими знаками-числами користувалися також і для одержання інших чисел. Так, якщо перед знаком X ставилась вертикальна риска, то отримували знак IX, який означав, що від десяти треба відняти одиницю і результат буде дорівнювати 9. Знаки, подібні X, називаються вузловими. Вони широко використовувалися в первісних непозиційних системах числення. Слід ще раз зазначити, що серед цих знаків не було такого, який би відповідав нулю. Це свідчить про те, що нуль у той час ще не був сформований як число.
Кількість чисел, яку можна було одержати з допомогою непозиційного кодування, через його складність і відповідно велику кількість чисел, що потребували запам'ятовування, була обмежена кількома сотнями, і, крім того, щодо цих чисел досить важко було виконувати арифметичні й логічні операції. Тому в подальшому з розвитком науки виникла потреба в більш ефективних системах числення, які б мали прості правила кодування чисел, та легко виконували б щодо них арифметичні й логічні операції. Такі системи чисел були створені і отримали назву позиційних. Більш докладно ці системи числення будуть розглянуті нижче, тому що вони складають на сьогодні основу теорії систем числення взагалі.
2.0 Позицiйнi системи числення
У позиційних системах числення одна і та ж цифра (числовий знак) у записі числа набуває різних значень залежно від своєї позиції. Таким чином, позиція цифри має вагу у числі. Здебільшого вага кожної позиції кратна деякому натуральному числу 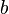 ,
,  , яке називається основою системи числення.
, яке називається основою системи числення.
|
|
|
Винахід позиційної системи числення, заснованої на помісному значенні цифр, приписують шумерам і вавилонцям. Її було розвинуто індусами і вона отримала неоціненні наслідки для історії людської цивилізації.
До числа таких систем належить сучасна Десяткова система числення (з основою 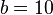 ), виникнення якої пов'язують із лічбою на пальцях. У середньовічній Європі вона з'явилася через італійських купців, які у свою чергу запозичили її у мусульман.
), виникнення якої пов'язують із лічбою на пальцях. У середньовічній Європі вона з'явилася через італійських купців, які у свою чергу запозичили її у мусульман.
2.1 Класифікація позиційних систем числення
З метою ефективного використання систем числення в теорії і на практиці важливо їх класифікувати. У першу чергу розглянемо системи числення, які генерують числа однакової довжини.
Системи числення з рівною довжиною чисел належать до класу рівномірних кодів. Однакову довжину числа мають лише тоді, коли підмножини, які отримують в системах числення на кожному кроці розбиття вихідної множини, містять однакове число елементів.
Такі системи числення назвемо однорідними. Їх також ще називають природними, або степеневими. Як уже зазначалось, характерною ознакою таких систем є однаковість їх чисел за довжиною. Крім цього, другою не менш важливою особливістю цих систем є те, що вага розрядів в них змінюється згідно зі степеневим законом. До цих систем числення належать двійкова, десяткова, п'ятерична і безліч подібних інших. За їх основи беруть числа 2, 10, 5 і т. д.
Розроблення більш складних, ніж однорідні, позиційних систем числення почалося в основному в другій половині 20-го століття після того, як з'явилася цифрова обчислювальна техніка. Такі системи назвемо неоднорідними. Вони використовувались здебільшого при побудові спеціалізованих обчислювачів, систем зв'язку та керування, кодуючих та декодуючих пристроїв з метою підвищення їх ефективності.
|
|
|
Найпростішими неоднорідними системами числення є системи, в яких кількість елементів в усіх підмножинах, отриманих на попередньому кроці розбиття, буде однаковою. При цьому встановлюється функціональний зв'язок між номером кроку розбиття й числом підмножин у розбитті на цьому кроці.
Ваги цифр, які належать до одного розряду числа, у цьому випадку рівні між собою, однак вони на відміну від однорідних систем числення змінюються від розряду до розряду не за степеневим законом, як це має місце для однорідних систем числення, а за більш складним. Числа для неоднорідних систем числення з такими обмеженнями мають, як і для однорідних, рівну довжину. Прикладом таких систем числення є факторіальні, а в більш загальному випадку системи зі змішаною основою, чи поліадичні. На рис. 1.1 у вигляді блок-схеми наведена класифікація позиційних систем числення.
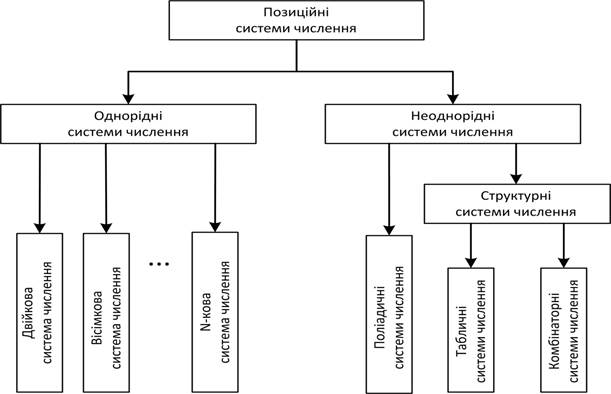
Таким чином, позиційні системи числення розподіляються на два великих класи — однорідні (з рівною довжиною чисел і основою в вигляді натурального числа) і неоднорідні (з рівною та нерівною довжиною чисел і більш складною основою, ніж натуральні числа). Однорідні системи числення відповідно до числа, яке взяте за їх основу, у свою чергу, поділяються на двійкові, трійкові, десяткові й т.д. Неоднорідні поділяються на системи зі змішаною основою, або поліадичні, і структурні — з числовою або функціональною основою. Останні, у свою чергу, поділяться на комбінаторні і табличні.
Всі позиційні системи числення без винятку можуть бути подані у вигляді дерев розбиття, вершини яких відображають кількість елементів у підмножинах, що розбиваються, а гілки — номери, що кодують підмножини, які виникають після розбиття. При цьому послідовності цих номерів утворюють числа позиційних систем числення. Номери в даному випадку є цифрами чисел.
|
|
|
|
|
Дата добавления: 2015-08-31; Просмотров: 736; Нарушение авторских прав?; Мы поможем в написании вашей работы!