
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Необходимые теоретические сведения
|
|
|
|
Пусть 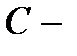 линейный
линейный 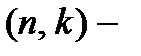 код над полем
код над полем 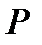 .
.
Определение 2.1. Матрица 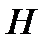 порядка
порядка 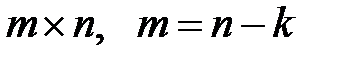 называется проверочной матрицей кода
называется проверочной матрицей кода  , если
, если 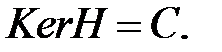
Отметим некоторые свойства проверочных матриц.
Свойство 1. Проверочная матрица у каждого линейного кода всегда существует.
Данное свойство следует из общего факта линейной алгебры: для всякого собственного подпространства 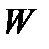 линейного пространства
линейного пространства 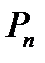 существует система линейных однородных уравнений, множество решений которой в точности совпадает с множеством векторов подпространства
существует система линейных однородных уравнений, множество решений которой в точности совпадает с множеством векторов подпространства 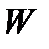 .
.
Если известна порождающая матрица 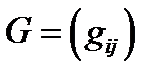 кода
кода 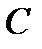 , то с помощью строк этой матрицы, а фактически базиса
, то с помощью строк этой матрицы, а фактически базиса 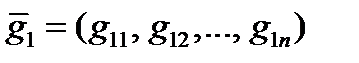 ,
, 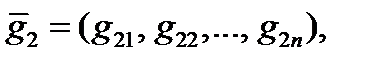
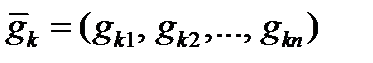 кода
кода 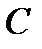 , можно составить систему линейных однородных уравнений:
, можно составить систему линейных однородных уравнений:
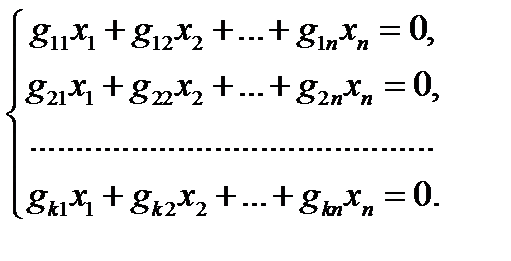 (2.1)
(2.1)
Множество решений системы (2.1) составляет ядро матрицы 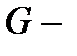 подпространство пространства
подпространство пространства 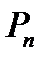 размерностью
размерностью 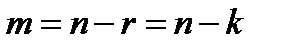 . Пусть
. Пусть 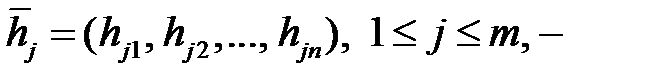 базис пространства решений системы (2.1). Тогда матрица
базис пространства решений системы (2.1). Тогда матрица
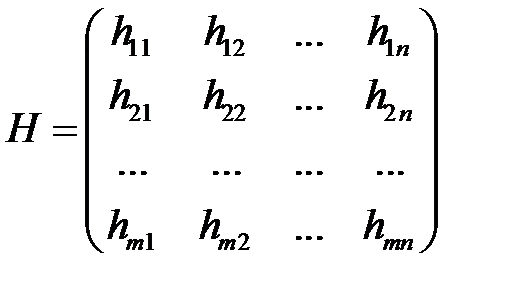 (2.2)
(2.2)
есть искомая проверочная матрица кода  . Действительно, в силу соотношений (2.1) должны выполняться равенства
. Действительно, в силу соотношений (2.1) должны выполняться равенства 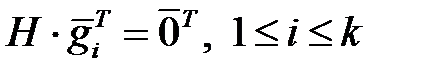 . Они означают, что
. Они означают, что 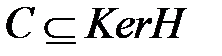 . С другой стороны,
. С другой стороны, 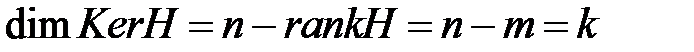 . Это означает, что
. Это означает, что 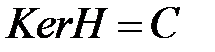 .
. 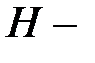 действительно является проверочнай матрицей кода
действительно является проверочнай матрицей кода  .
.
Свойство 2. Координаты базиса ядра матрицы 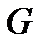 составляют проверочную
составляют проверочную  матрицу
матрицу 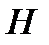 кода
кода 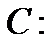 только для векторов
только для векторов 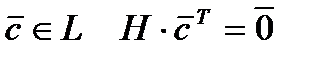 и только для них.
и только для них.
Свойство 3.  ;
; 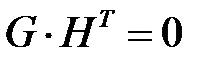 .
.
Пример 2.1. Код 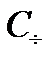 с проверкой на чётность из примера 1.2 состоит из векторов-решений единственного уравнения
с проверкой на чётность из примера 1.2 состоит из векторов-решений единственного уравнения 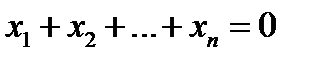 над полем
над полем 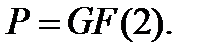 Следовательно, проверочная матрица кода
Следовательно, проверочная матрица кода 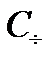 есть
есть 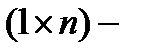 матрица и имеет вид:
матрица и имеет вид: 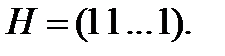
Пример 2.2. В силу сказанного выше, матрица коэффициентов системы линейных уравнений (1.3)
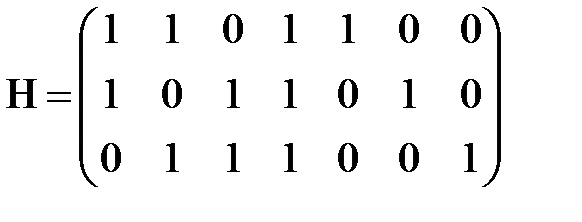
|
есть проверочная матрица 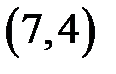 – кода Хемминга, определенного в примере 1.3. Так как базисный минор матрицы
– кода Хемминга, определенного в примере 1.3. Так как базисный минор матрицы 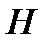 расположен в последних трех столбцах, то
расположен в последних трех столбцах, то 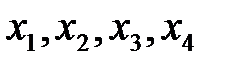 являются свободными переменными системы линейных уравнений (1). Отсюда легко получаем порождающую матрицу кода Хемминга:
являются свободными переменными системы линейных уравнений (1). Отсюда легко получаем порождающую матрицу кода Хемминга:
|
|
|
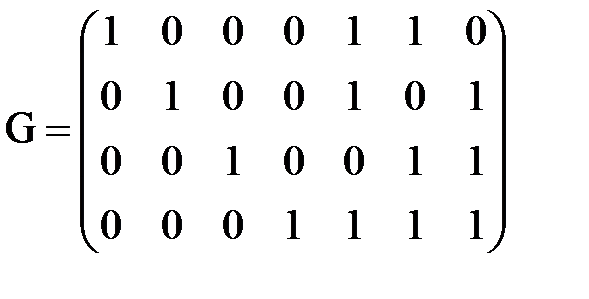 . .
|
Проверочная матрица кода определена не однозначно.
Свойство 4. Пусть 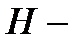 матрица порядка
матрица порядка 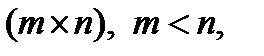 и ранга
и ранга 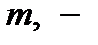 проверочная матрица линейного
проверочная матрица линейного 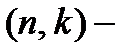 кода
кода 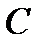 , где
, где 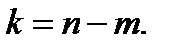 Тогда для всякой невырожденной квадратной матрицы
Тогда для всякой невырожденной квадратной матрицы 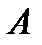 порядка
порядка 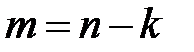 матрица
матрица 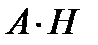 также является проверочной для кода
также является проверочной для кода 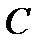 .
.
Данное свойство дополняет свойство, указанное ниже.
Свойство 5. Пусть 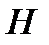 и
и 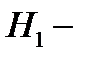 две проверочные матрицы линейного
две проверочные матрицы линейного 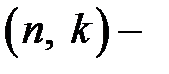 кода
кода  . Тогда существует квадратная
. Тогда существует квадратная 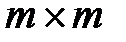 – матрица
– матрица 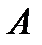 для
для 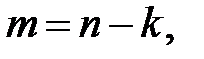 такая, что
такая, что 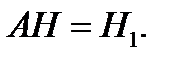
Каждая из матриц 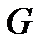 или
или 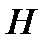 однозначно определяет код
однозначно определяет код 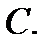
Из свойств 3 и 4 следует критерий для определения, когда две матрицы являются проверочными матрицами одного и того же линейного кода.
Теорема 2.1. Пусть 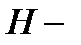 проверочная
проверочная 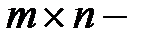 матрица линейного
матрица линейного 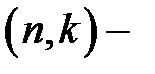 кода
кода  . Матрица
. Матрица 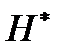 порядка
порядка 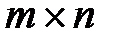 является проверочной матрицей этого же кода тогда и только тогда, когда найдется такая невырожденная
является проверочной матрицей этого же кода тогда и только тогда, когда найдется такая невырожденная 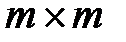 – матрица
– матрица 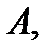 что
что 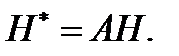
Свойство 6. Количество различных проверочных матриц линейного 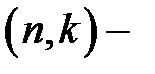 кода над конечным полем
кода над конечным полем 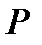 совпадает с количеством различных невырожденных квадратных матриц порядка
совпадает с количеством различных невырожденных квадратных матриц порядка 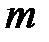 в поле
в поле 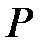 , то есть с порядком группы
, то есть с порядком группы 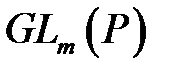 невырожденных квадратных матриц порядка
невырожденных квадратных матриц порядка 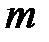 над полем
над полем 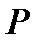 .
.
Свойство 6 позволяет определить количество проверочных матриц у данного линейного кода над конечным полем  . Так, над полем
. Так, над полем 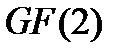 из двух элементов, по теореме 4.11 [11], группа матриц
из двух элементов, по теореме 4.11 [11], группа матриц 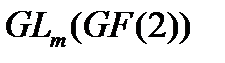 имеет порядок
имеет порядок 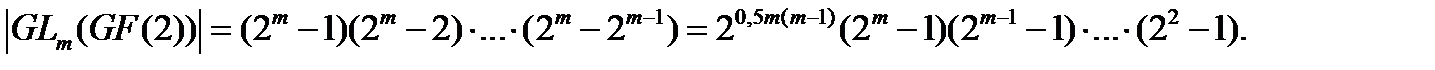 В частности, при
В частности, при 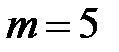 этот порядок равен
этот порядок равен 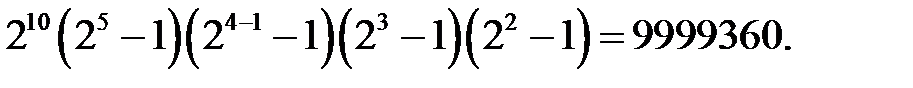 При
При 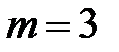 искомый порядок равен
искомый порядок равен 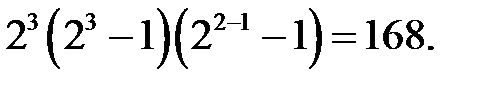 Это означает, что у
Это означает, что у 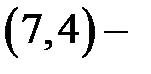 кода Хемминга над полем
кода Хемминга над полем 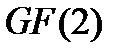 имеется 168 различных проверочных матриц.
имеется 168 различных проверочных матриц.
Определение 2.2. Метрикой или расстоянием на множестве 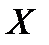 называется определённая на декартовом квадрате
называется определённая на декартовом квадрате 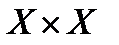 функция
функция 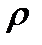 с неотрицательными действительными значениями, удовлетворяющая при любых
с неотрицательными действительными значениями, удовлетворяющая при любых 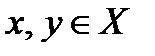 условиям
условиям
1)  тогда и только тогда, когда
тогда и только тогда, когда 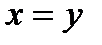 (аксиома тождества);
(аксиома тождества);
2) 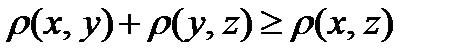 (аксиома треугольника);
(аксиома треугольника);
3) 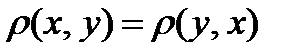 (аксиома симметрии).
(аксиома симметрии).
Хемминг весьма удачно предложил свою метрику на векторных пространствах с координатами в полях Галуа. Пусть 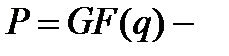 конечное поле из
конечное поле из 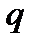 элементов,
элементов,  векторное
векторное 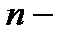 мерное пространство над полем
мерное пространство над полем 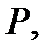 содержащее линейный
содержащее линейный 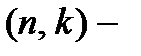 код
код 
|
|
|
Определение 2.3. Расстоянием Хемминга между векторами 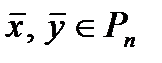 называется количество
называется количество 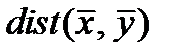 несовпадающих координат этих векторов.
несовпадающих координат этих векторов.
Весом 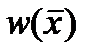 вектора
вектора 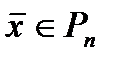 называется количество ненулевых координат этого вектора.
называется количество ненулевых координат этого вектора.
Несложно видеть, что расстояние Хэмминга между векторами 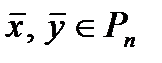 равно весу вектора
равно весу вектора 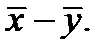 Очевидно,
Очевидно, 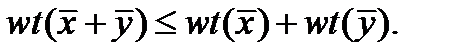
Лемма 2.1. Расстояние Хэмминга обладает всеми свойствами обычного расстояния
1) 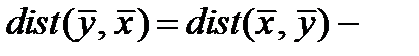 свойство симметричности;
свойство симметричности;
2) 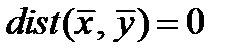 тогда и только тогда, когда
тогда и только тогда, когда 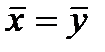 ;
;
3) 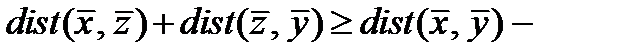 неравенство треугольника.
неравенство треугольника.
Определение 2.4. 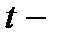 окрестностью вектора
окрестностью вектора 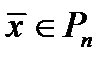 назовём совокупность всех векторов
назовём совокупность всех векторов 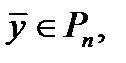 для которых
для которых 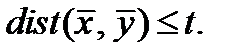
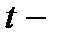 окрестности обладают обычным свойством отделимости.
окрестности обладают обычным свойством отделимости.
Лемма 2.2. Если 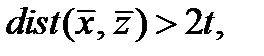 то
то 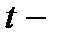 окрестности векторов
окрестности векторов 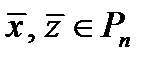 не пересекаются.
не пересекаются.
Определение 2.5. Минимальным или кодовым расстоянием кода 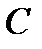 называется наименьшее из расстояний между попарно различными векторами кода
называется наименьшее из расстояний между попарно различными векторами кода 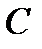 .
.
Из равенства 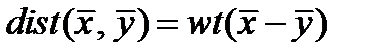 следует, что минимальное расстояние линейного кода равно наименьшему из весов ненулевых векторов этого кода.
следует, что минимальное расстояние линейного кода равно наименьшему из весов ненулевых векторов этого кода.
Значение кодового расстояния определяет следующая фундаментальная в помехоустойчивом кодировании теорема.
Теорема 2.2. Если минимальное расстояние кода 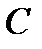 равно
равно 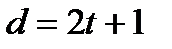 или
или 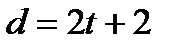 , то код
, то код 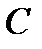 может обнаружить до
может обнаружить до 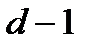 ошибок и исправить до
ошибок и исправить до 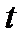 ошибок в каждом принятом векторе-слове длиной
ошибок в каждом принятом векторе-слове длиной 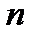 .
.
Следующая теорема служит критерием для определения минимального расстояния кода.
Теорема 2.3. Пусть 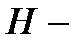 проверочная матрица двоичного кода
проверочная матрица двоичного кода 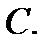 Минимальное расстояние этого кода равно
Минимальное расстояние этого кода равно 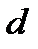 тогда и только тогда, когда любые
тогда и только тогда, когда любые 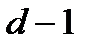 столбцов матрицы
столбцов матрицы 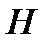 линейно независимы, но найдутся
линейно независимы, но найдутся 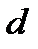 линейно зависимых столбцов.
линейно зависимых столбцов.
Доказательство теоремы обеспечивает
Лемма 2.3. Пусть 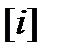 это i –ый столбец проверочной матрицы
это i –ый столбец проверочной матрицы 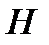 линейного кода
линейного кода 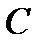 над полем
над полем 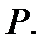 Вектор
Вектор 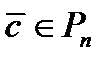 весом
весом 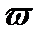 с ненулевыми координатами на позициях
с ненулевыми координатами на позициях 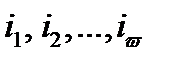 принадлежит коду
принадлежит коду 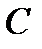 тогда и только тогда, когда система столбцов
тогда и только тогда, когда система столбцов 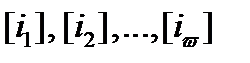 линейно зависима.
линейно зависима.
Одним из важнейших понятий теории помехоустойчивых кодов является синдром ошибок. В процессе передачи информации на кодовое слово 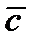 может наложиться «шум» вектор-ошибок
может наложиться «шум» вектор-ошибок 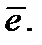 В результате приемное устройство получает искажённое сообщение
В результате приемное устройство получает искажённое сообщение 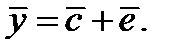
Определение 2.6. Синдромом ошибок принятого слова 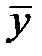 в коде С с проверочной матрицей
в коде С с проверочной матрицей 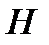 называется вектор
называется вектор 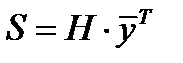 .
.
|
|
|
Если 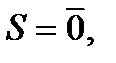 то
то 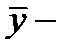 кодовое слово. Следовательно, условие
кодовое слово. Следовательно, условие 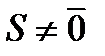 служит признаком наличия ошибочных символов в принятом слове
служит признаком наличия ошибочных символов в принятом слове 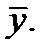 В силу ассоциативности операций сложения и умножения матриц синдром
В силу ассоциативности операций сложения и умножения матриц синдром  . Это означает, что
. Это означает, что 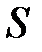 зависит только от вектора ошибок
зависит только от вектора ошибок 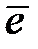 и не зависит от кодовых слов.
и не зависит от кодовых слов.
Пусть 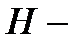 фиксированная проверочная матрица данного линейного
фиксированная проверочная матрица данного линейного 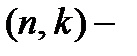 кода
кода 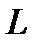 над полем
над полем 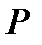 . Пусть
. Пусть  пространство всех векторов размерности
пространство всех векторов размерности 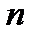 над полем
над полем 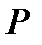 – пространство возможных ошибок кода
– пространство возможных ошибок кода 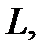 содержащее
содержащее 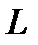 в качестве своего подпространства.
в качестве своего подпространства.
Предложение 2.1. Если 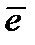 пробегает все векторы пространства En, то
пробегает все векторы пространства En, то 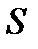 пробегает все векторы пространства E n-k.
пробегает все векторы пространства E n-k.
Следствие. Пусть 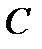 – линейный
– линейный 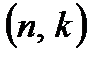 – код над конечным полем из
– код над конечным полем из 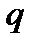 элементов. Тогда каждое значение синдрома
элементов. Тогда каждое значение синдрома  принимают в точности
принимают в точности 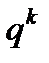 различных векторов-ошибок, а именно векторы
различных векторов-ошибок, а именно векторы 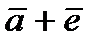 для всех
для всех 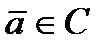 и только они.
и только они.
Пусть 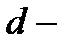 минимальное расстояние кода
минимальное расстояние кода 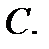 Пусть
Пусть 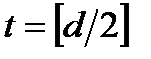 , если
, если 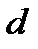 нечетно, и
нечетно, и 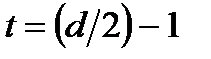 , если
, если 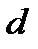 четно. Пусть
четно. Пусть 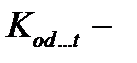 множество всех векторов весом
множество всех векторов весом 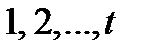 в пространстве
в пространстве 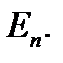
Предложение 2.2. Если 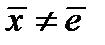 для
для 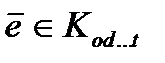 , но
, но 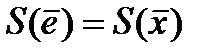 , то
, то 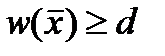 . Следовательно, для произвольных
. Следовательно, для произвольных 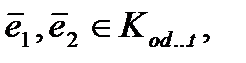
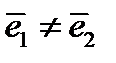 , их синдромы попарно различны:
, их синдромы попарно различны:  .
.
Предложение 2.2 вместе с очевидной уверенностью, что наиболее вероятны ошибки малого веса, создают теоретическую базу для синдромных методов коррекции ошибок по значениям синдромов ошибок, определяющих соответствующие векторы ошибок из множества 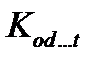 . Основные преимущества синдромных методов в следующем:
. Основные преимущества синдромных методов в следующем:
1) согласно предложению 2.2 синдромы однозначно соответствуют ошибкам декодируемого многообразия;
2) синдромы имеют существенно меньшие размеры по сравнению с кодовыми словами и векторами ошибок (что особенно наглядно для высокоскоростных кодов, например для кодов Хемминга);
3) для нахождения синдромов не требуется специальных вычислений, кроме обусловленных необходимостью индикации наличия или отсутствия ошибок в принятом блоке-сообщении;
4) синдром совершенно не связан с передаваемой информацией, а исключительно только с произошедшей ошибкой.
|
|
|
|
|
Дата добавления: 2017-02-01; Просмотров: 96; Нарушение авторских прав?; Мы поможем в написании вашей работы!